Endomorphism semi-group
A semi-group consisting of the endomorphisms of a certain object (a set $X$ endowed with some structure $\sigma$) with the operation of multiplication (performing transformations in succession). The object $X$ can be a vector space, a topological space, an algebraic system, a graph, etc.; it is usually regarded as an object of a certain category, and as a rule, the morphisms (cf. Morphism) in this category are the mappings preserving the relations of 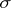 (linear or continuous transformations, homomorphisms, etc.). The set $\operatorname{End}X$ of all endomorphism of $X$ (that is, of morphisms to its subobjects) is a sub-semi-group of the semi-group $T_X$ of all transformations of $X$ (see Transformation semi-group).
(linear or continuous transformations, homomorphisms, etc.). The set $\operatorname{End}X$ of all endomorphism of $X$ (that is, of morphisms to its subobjects) is a sub-semi-group of the semi-group $T_X$ of all transformations of $X$ (see Transformation semi-group).
The semi-group $\operatorname{End}X$ may include a considerable amount of information on the structure $\sigma$. For example, if $X$ and $Y$ are vector spaces of dimensions $\geq2$ over skew-fields $F$ and $H$, respectively, then if the semi-groups $\operatorname{End}X$ and $\operatorname{End}Y$ of their endomorphisms (that is, linear transformations) are isomorphic, it follows that $X$ and $Y$ (and in particular, $F$ and $H$) are isomorphic. Some pre-ordered sets and lattices, every Boolean ring, and some other algebraic systems are determined up to isomorphism by their endomorphism semi-groups. The same is true for some modules and transformation semi-groups. Similar information about $X$ is carried by certain proper sub-semi-groups of $\operatorname{End}X$ (for example, the semi-groups of homeomorphic transformations of a topological space).
Some classes of objects $X$ (for example, topological spaces) can be characterized in this manner by their semi-groups of partial endomorphisms, that is, partial transformations of $X$ that are morphisms of their subobjects.
References
| [1] | L.M. Gluskin, "Transformation semigroups" , Proc. 4-th All-Union Math. Congress , 2 , Leningrad (1964) pp. 3–9 (In Russian) |
| [2] | A.A. Zykov, "The theory of finite graphs" , 1 , Novosibirsk (1969) (In Russian) |
| [3] | K.D. Magill, "A survey of semigroups of continuous selfmaps" Semigroup Forum , 11 (1975–1976) pp. 189–282 |
| [4] | M. Petrich, "Rings and semigroups" , Springer (1974) |
Endomorphism semi-group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Endomorphism_semi-group&oldid=34012