Double point

A kind of singular point of a curve $F(x,y)=0$ at which the first partial derivatives are zero, and at least one second partial derivative of the function $F(x,y)$ is non-zero. In studying the structure of the curve near a double point one considers the sign of the expression

$$\Delta=\left(\frac{\partial^2F}{\partial x^2}\right)_0\left(\frac{\partial^2F}{\partial y^2}\right)_0-\left(\frac{\partial^2F}{\partial x\partial y}\right)_0^2.$$

If $\Delta>0$, the double point is said to be an isolated point; thus, the coordinate origin of the curve

$$y^2-x^4+4x^2=0$$

is an isolated double point (Fig. a). If $\Delta<0$, the double point is said to be a nodal point or a point of self-intersection; e.g. for the curve

$$(x^2+y^2+a^2)^2-4a^2x^2-a^4=0$$

the coordinate origin is a nodal point (cf. Fig. b).

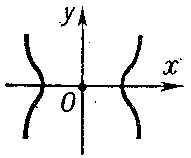
Figure: d033950a

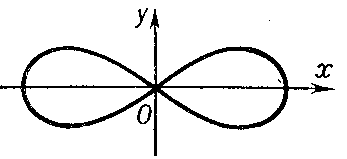
Figure: d033950b

If $\Delta=0$, the double point is either isolated or else is characterized by the fact that the different branches of the curve have a common tangent at the point; thus, a) at a cusp of the first kind the branches of the curve are situated on different sides of the common tangent and on the same side of their common normal (see, for example, Fig. c: $y^2-x^3=0$);

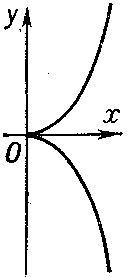
Figure: d033950c

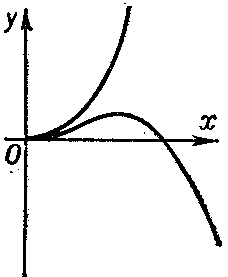
Figure: d033950d

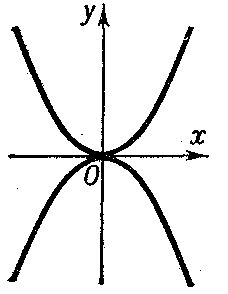
Figure: d033950e

b) at a cusp of the second kind the branches of the curve are situated on the same side of the common tangent and on the same side of the common normal (see, for example, Fig. d: $(y-x)^2-x^5=0$); and c) at a point of osculation the branches of the curve osculate (see, for instance, Fig. e: $y^2-x^4=0$).

Comments

A double point on an algebraic variety is a point of multiplicity two (cf. Multiplicity of a singular point).

References

[a1]	W. Fulton, "Algebraic curves" , Benjamin (1969) pp. 66

🛠️ This page contains images that should be replaced by better images in the SVG file format. 🛠️