Dinostratus quadratrix
A transcendental plane curve which is given in orthogonal Cartesian coordinates by:
$$y=x\operatorname{cotan}\frac{\pi x}{2a},$$
and in polar coordinates by
$$\rho=\frac{a(\pi-2\phi)}{\pi\cos\phi}.$$
A Dinostratus quadratrix has an infinite number of branches (see Fig.), intersecting the $x$-axis at the points $x=\pm a,\pm3a,\pm5a,\ldots,$ with asymptotes $x=\pm2a,\pm4a,\pm6a,\ldots$. The points of intersection with the straight line $y=2a/\pi$ are points of inflection.
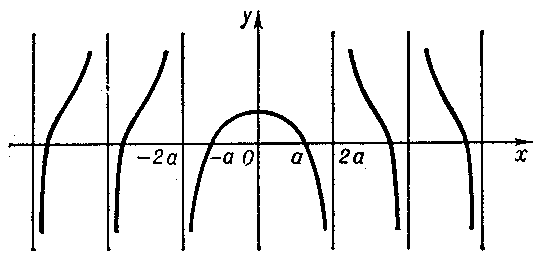
Figure: d032560a
The first considerations of the quadratrix are attributed to Hippias of Elis (420 B.C.). Dinostratus (second half of the 4th century B.C.) showed that the problem of the quadrature of the circle can be graphically solved with the aid of the quadratrix.
Comments
For the reason mentioned in the last lines of the article above, this curve is also called Hippias' quadratrix, or the quadratrix of Hippias, cf. [a1].
References
| [a1] | J.D. Lawrence, "A catalog of special plane curves" , Dover (1972) ISBN 0-486-60288-5 Zbl 0257.50002 |
| [a2] | K. Fladt, "Analytische Geometrie spezieller ebener Kurven" , Akad. Verlagsgesell. (1962) |
Dinostratus quadratrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dinostratus_quadratrix&oldid=53790