Differential equations, ordinary, with distributed arguments

ordinary differential equations with deviated arguments, ordinary differential equations with deviating arguments

Ordinary differential equations connecting the argument, the unknown function and its derivatives generally taken for different values of the argument. Examples are:

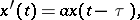(1)

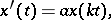(2)

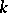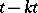where the constants , and are given; in equation (1) and in equation (2) are the deviations, retardations or lags of the arguments. There are also more complicated differential equations with a large number of deviations of the argument, which may represent given functions (in particular, if they are constant, the equation is often referred to as a differential-difference equation) or may even depend on the solution sought. There were also sporadic studies of differential equations with deviated arguments in which the unknown function depends on more than one argument. Differential equations with deviated arguments first appeared in connection with the formal solution of partial differential equations, and were subsequently studied for their own sake, in the context of geometrical problems, and later in various applications, mainly in automatic control theory. A systematic construction of the theory of ordinary differential equations with deviated arguments was begun in 1949.

The definition of differential equations with deviated arguments permits any superpositions of the sought solution (of the type 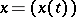) and its integrals; formally the class of ordinary differential equations with deviated arguments includes all equations of mathematical analysis. Nevertheless, ordinary differential equations with deviated arguments are usually understood to mean some natural class of ordinary differential equations in which a deviation of the argument, permitting the construction of a meaningful theory, has been introduced. Several properties of such equations are directly analogous to those of ordinary differential equations, while other properties are principally new.

An equation (or a system of equations)

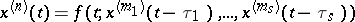(3)

(for a system, and 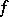are vectors), where all 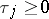, is said to be an equation (system) of retarded (lag), neutral, or leading type if 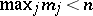, , 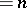, 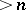respectively. Equations of other forms are classified in this way on the base of a transformation into the form (3) by the substitution 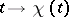, where 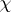is an increasing function; for instance, equation (1) is of retarded type if 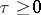and is of leading type (by the substitution 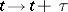) if 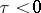. If the deviations 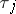depend on 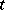, equation (3) may change type; then equation (2) with 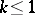is of retarded type if 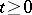and is of leading type 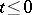if . If 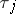depends on the solution sought, equation (3) may be of different types for different solutions. The theory of differential equations with deviated arguments of retarded type is developed in most detail, that of neutral type is developed to a lesser extent, while that of leading type has not been studied to any significant extent.

The following is one of the simplest classes of differential equations with deviated arguments:

(4)

The following fundamental initial value problem is formulated for this class of equations: Given an initial point 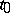, an initial function 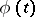, , 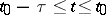and a value 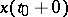; the solution of this problem for equation (4) is understood to be a function 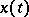, , 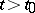such that equation (4) holds identically, and if 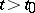, , 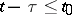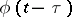is to be substituted for 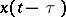in the right-hand side of the equation. The problem may be solved by the method of steps: If 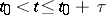, one solves the initial value problem for equation (4) in which 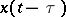is replaced by 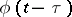; if 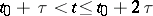, one has 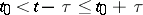, i.e. one has already constructed 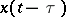, etc. Thus, each step consists in solving a Cauchy problem for an equation without a deviating argument. If the two functions 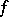and 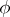are continuous and 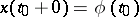, the solution of the problem exists on some interval 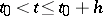and may be extended in the usual way, and if the function 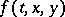satisfies a Lipschitz condition with respect to , this solution is unique and depends continuously on 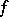, 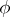and . If, in addition, the function 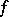is sufficiently smooth, 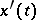is continuous for 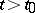, 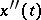is continuous if 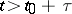, etc. (the smoothing property).

The initial value problem is formulated and the solution is constructed for systems of equations of the form (4) and for equations of higher orders in a completely similar manner. If several lags are present, the smallest one is taken as the step. If 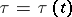, 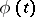should be defined on an entire initial set of values 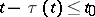, . If 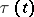has zeros the method of steps cannot be employed, but it is possible to prove the solvability of the initial value problem, similar to the one stated above, if simple approximation or iteration methods are employed. The numerical methods of solution are the same, in principle, as for 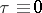. If the given functions are discontinuous or if 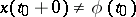, the concept of a solution can be naturally extended.

The solution of the formulated initial value problem is constructed in the increasing direction of 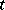only. Another feature of it is that the manifold of solutions for arbitrary 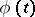is usually infinite-dimensional. (Equations without pre-history, for which 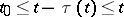if 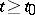, such as equation (2) for 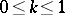, , are an exception to this rule.) This is a significant difference between the theory of differential equations with deviated arguments and the theory of differential equations without deviated arguments.

In equation (4) the lag is concentrated. There are also equations with deviated lags, the right-hand side of which contains the integrals

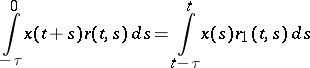(these are Volterra-type integro-differential equations) or, in the combined case,

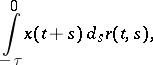etc. The most common type of first-order differential equation with deviated arguments of retarded type is the differential-functional Volterra-type equation:

where the right-hand side is a functional for any 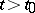. The initial value problem is solvable for such equations as well.

For differential equations with deviated arguments of neutral type, for example

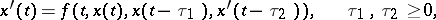the formulation and the properties of the initial value problems resemble those given above, but there is no smoothing property; complexities may occur if the variable lag 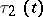has zeros. The initial value problem is ill-posed for differential equations with deviated arguments of leading type.

Linear autonomous differential equations with deviated arguments (i.e. equations in which the coefficients and the deviations of the argument are constant) have been studied in most detail. The equation (without constant term)

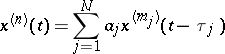(5)

(all 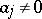) has particular solutions 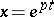, where 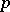satisfies the characteristic equation

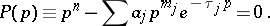(6)

Here is a quasi-polynomial; the solutions 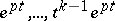of equation (5) correspond to a 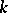-fold root of equation (6). If even a single 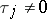, equation (6) has an infinite number of roots 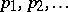. A necessary and sufficient condition for equation (5) to be of retarded (neutral) type is

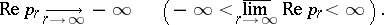In such a case each solution of equation (5) has a series expansion in the particular solutions given above, and methods of ordinary operational calculus may be employed in solving the initial value problem for equation (5) and the corresponding inhomogeneous equation. Systems of equations and equations with deviated lags display similar properties.

The usual conditions for stability of a solution are directly extended to differential equations with deviated arguments of retarded and neutral types. The condition

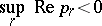is necessary and sufficient for the asymptotic stability of solutions of equation (5). If this condition is met, the zero solution of non-linear autonomous equations, for which equation (5) is a linear approximation, is also asymptotically stable.

The method of Lyapunov functions for the study of the stability of differential equations with deviated arguments was extended by N.N. Krasovskii [5]. He suggested the use of the functionals 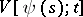on 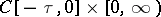; the total derivative of such a functional "along the solution" of a given equation of the type (4) may be computed by virtue of this equation, and it represents a functional of the same type, i.e.

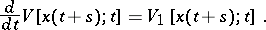The analogue of Lyapunov's stability theorem is as follows: If

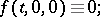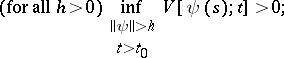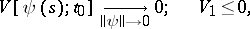then the trivial solution of equation (4) is stable. The main stability theorems, expressed in such terms, have a converse.

Several results have been obtained for periodic differential equations with deviated arguments. Thus, if

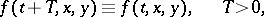the fixed points of the operator

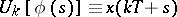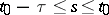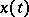(; is the solution of equation (4) for the initial function 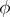; 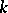is a natural number) determine the 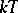-periodic solutions of equation (4). Owing to this and to a number of similar facts, it is possible to apply methods of the theory of non-linear operators to find periodic solutions and to clarify their stability. For the case of linear homogeneous 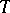-periodic differential equations with deviated arguments of retarded type, it proved possible to approximate each solution to a desired degree of accuracy in the scale of exponents by linear combinations of solutions of the form

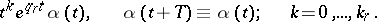Other trends in the study of differential equations with deviated arguments include: a detailed study of asymptotic and oscillation properties of equations

and analogous equations of the second order; obtaining asymptotic expressions for the solutions of systems with small deviations of the argument or with a small non-linearity; the extension of the asymptotic Krylov–Bogolyubov methods to differential equations with deviated arguments (cf. Krylov–Bogolyubov method of averaging); a similar extension of L.S. Pontryagin's method of optimal control (cf. Optimal control, mathematical theory of); the study of boundary value problems; the study of partial differential evolution equations with time lag (cf. Evolution equation); the study of stochastic differential equations with deviated arguments (cf. Stochastic differential equation), etc.

References

[1]	L.E. El'sgol'ts, S.B Norkin, "Introduction to the theory and application of differential equations with deviating arguments" , Acad. Press (1973) (Translated from Russian)
[2]	E. Pinney, "Ordinary difference-differential equations" , Univ. California Press (1958)
[3]	R. Bellman, C.L. Cooke, "Differential-difference equations" , Acad. Press (1963)
[4]	A.D. Myskis, "Linear differential equations with retarded argument" , Moscow (1972) (In Russian)
[5]	N.N. Krasovskii, "Stability of motion. Applications of Lyapunov's second method to differential systems and equations with delay" , Stanford Univ. Press (1963) (Translated from Russian)
[6]	S.B. Norkin, "Differential equations of the second-order with retarded argument" , Amer. Math. Soc. (1972) (Translated from Russian)
[7]	V.P. Rubanik, "Oscillations of quasi-linear systems with retardment" , Moscow (1969) (In Russian)
[8]	M.N. Oĝuztöreli, "Time-lag control systems" , Acad. Press (1966)
[9]	A. Halanay, "Differential equations: stability, oscillations, time-lags" , Acad. Press (1966)
[10]	J.K. Hale, "Functional differential equations" , Springer (1971)

Comments

Another, rather striking, difference between differential equations (without constant term) with delays and ordinary differential equations is that the former may have non-zero solutions 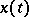such that 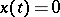for all 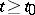for some 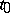. This can happen, for instance, for systems of delay equations 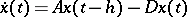when the matrix 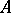is singular and non-zero.

References

[a1]	S.-N. Chow, J.K. Hale, "Methods of bifurcation theory" , Springer (1982)
[a2]	H.-O. Peitgen (ed.) H.-O. Walther (ed.) , Functional differential equations and approximation of fixed points , Lect. notes in math. , 730 , Springer (1979)