Convexity
A term used in various branches of mathematics and indicating properties which generalize some properties of convex sets (cf. Convex set) in Euclidean spaces  . The applicability of a number of methods of study is connected with the term "convexity" .
. The applicability of a number of methods of study is connected with the term "convexity" .
The following two basic definitions are almost equivalent in  . A set is convex: 1) if it is the intersection of open half-spaces; or 2) if it contains with two arbitrary points the segment connecting these points. Both definitions of convexity are applied to the case of vector spaces
. A set is convex: 1) if it is the intersection of open half-spaces; or 2) if it contains with two arbitrary points the segment connecting these points. Both definitions of convexity are applied to the case of vector spaces  .
.
Definition 2) is generalized to include sets in spaces with geodesics (spaces with a connection; locally compact metric spaces, in particular Riemannian and Finsler spaces). The geodesics play the role of segments, but if the two points can be connected by non-unique geodesics or by shortest curves, the concept of convexity branches into several possible meanings. In Riemannian geometry, in particular, the following modifications of convexity are employed [1], [2]:
a set  is convex if any two points of
is convex if any two points of  can be connected by a unique shortest curve and if this shortest curve is contained in
can be connected by a unique shortest curve and if this shortest curve is contained in  ;
;
a set  is locally convex if each point of
is locally convex if each point of  has a neighbourhood in
has a neighbourhood in  which is convex in the sense of ;
which is convex in the sense of ;
a set  is weakly convex if any two points can be connected by at least one shortest curve lying in
is weakly convex if any two points can be connected by at least one shortest curve lying in 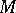 ; and
; and
a set 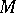 is absolutely convex if all geodesics connecting any two points are located in
is absolutely convex if all geodesics connecting any two points are located in  .
.
The boundary (or part of the boundary) of an  -dimensional convex body in
-dimensional convex body in  is called a convex hypersurface; if
is called a convex hypersurface; if 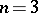 , it is called a convex surface, if
, it is called a convex surface, if 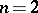 , it is said to be a convex curve.
, it is said to be a convex curve.
For a function of a real variable convexity signifies the convexity of its supergraph (cf. Convex function (of a real variable)). The convexity of a functional 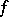 on
on  is defined in a similar manner (cf. Convex functional).
is defined in a similar manner (cf. Convex functional).
For convex sets in  one can speak of the convexity of a family
one can speak of the convexity of a family  of sets:
of sets:  is convex if
is convex if 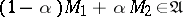 provided that
provided that 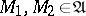 ,
,  . Convex (and concave) functionals
. Convex (and concave) functionals  can be defined on convex families
can be defined on convex families  . Convexity of a functional is defined by the requirement
. Convexity of a functional is defined by the requirement
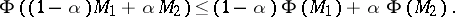 |
The term "convexity" as applied to univalent functions of a complex variable has a special meaning — the property of mapping the unit disc onto a convex domain (cf. Convex function (of a complex variable)).
The 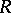 -convexity of a compactum
-convexity of a compactum  , meaning that each point with distance to
, meaning that each point with distance to 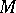 less than
less than 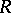 has a unique nearest point in
has a unique nearest point in 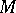 , is one generalization of convexity in
, is one generalization of convexity in  which has been studied [4], [5].
which has been studied [4], [5].
In the theory of linear differential operators the term "convexity" is connected with certain properties of homology groups [6]. This is connected with the possibility of touching the boundary from inside a domain by a hypersurface for which a certain number of principal curvatures is positive. In the theory of functions of several complex variables an important role is played by holomorphic convexity, which is connected with the impossibility of touching the boundary of a domain from inside with an analytic surface [7]. The last-named concept is a special case of  -convexity [7]. To the concept of
-convexity [7]. To the concept of 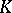 -convexity one can transfer many given convexity properties.
-convexity one can transfer many given convexity properties.
The concept of 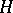 -convexity is employed in convex analysis; it is a generalization of the representability of a convex function as the supremum of a family of linear functions [8].
-convexity is employed in convex analysis; it is a generalization of the representability of a convex function as the supremum of a family of linear functions [8].
In the theory of metric spaces, (Menger) convexity of a metric is defined as follows: For any points  there exists a third point
there exists a third point  for which
for which 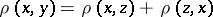 [9].
[9].  -convexity of a set
-convexity of a set  means that moreover
means that moreover  belongs to
belongs to 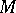 if
if 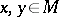 . Definitions of convexity in ordered spaces (cf. Convex subgroup) are very similar.
. Definitions of convexity in ordered spaces (cf. Convex subgroup) are very similar.
To almost each definition of convexity there corresponds a concept of local convexity. However, for the class of locally convex topological vector spaces, the term "local convexity" has a special meaning, namely, that for each point there exists a basis system of convex neighbourhoods.
References
| [1] | D. Gromoll, W. Klingenberg, W. Meyer, "Riemannsche Geometrie im Grossen" , Springer (1968) |
| [2] | A.D. Aleksandrov, V.A. Zalgaller, "Intrinsic geometry of surfaces" , Transl. Math. Monogr. , Amer. Math. Soc. (1967) (Translated from Russian) |
| [3] | H. Hadwiger, "Vorlesungen über Inhalt, Oberfläche und Isoperimetrie" , Springer (1957) |
| [4] | H. Federer, "Curvature measures" Trans. Amer. Math. Soc. , 93 (1959) pp. 418–491 |
| [5] | Yu.G. Reshetnyak, "On a generalization of convex surfaces" Mat. Sb. , 40 (82) : 3 (1956) pp. 381–398 (In Russian) |
| [6] | V.P. Palamodov, "Linear differential operators with constant coefficients" , Springer (1970) (Translated from Russian) |
| [7] | V.S. Vladimirov, "Methods of the theory of functions of several complex variables" , M.I.T. (1966) (Translated from Russian) |
| [8] | S.S. Kutateladze, A.M. Rubinov, "Minkowski duality and applications" Russian Math. Surveys , 27 : 3 (1972) pp. 137–191 Uspekhi Mat. Nauk , 27 : 3 (1972) pp. 127–176 |
| [9] | L. Danzer, B. Grünbaum, V.L. Klee, "Helly's theorem and its relatives" V.L. Klee (ed.) , Convexity , Proc. Symp. Pure Math. , 7 , Amer. Math. Soc. (1963) pp. 101–180 |
Comments
Definitions 1) and 2) are equivalent for most, but not all, sets. E.g., a convex set in the sense of 2), maximal with the property of not containing a given point, does not satisfy 1). An explicit example is the space 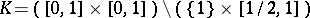 , the unit square minus one half of an edge. The space
, the unit square minus one half of an edge. The space  satisfies 2), but does not satisfy 1).
satisfies 2), but does not satisfy 1).
A more usual definition of convexity of a metric 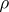 : For any
: For any 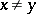 ,
, 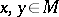 , and any
, and any 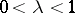 there is a
there is a 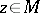 so that
so that
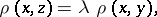 |
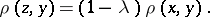 |
General results on convexity can be found in [a1], [a6]. Convexity also plays an important role in optimization theory, variational problems and the geometry of numbers (cf. [a2], [a3], [a5], [a7] and [a8]).
For holomorphic convexity cf. Stein manifold; the phrase "K-convex" is also used to denote the property of a set that each connected component is convex ([a4]); cf. Geometry of immersed manifolds for the notion of a 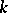 -convex surface.
-convex surface.
References
| [a1] | E.M. Alfsen, "Compact convex sets and boundary integrals" , Springer (1971) |
| [a2] | J.T. Marti, "Konvexe Analysis" , Birkhäuser (1977) |
| [a3] | R.T. Rockafellar, "Convex analysis" , Princeton Univ. Press (1969) |
| [a4] | F.A. Valentine, "Convex sets" , McGraw-Hill (1964) |
| [a5] | I. Ekeland, R. Teman, "Convex analysis and variational problems" , North-Holland (1976) |
| [a6] | G. Choquet, "Lectures on analysis" , 1–3 , Benjamin (1969) (Translated from French) |
| [a7] | P.M. Gruber, C.G. Lekkerkerker, "Geometry of numbers" , North-Holland (1987) (Updated reprint) |
| [a8] | V. Barbu, Th. Precupanu, "Convexity and optimization in Banach spaces" , Reidel (1986) |
Convexity. Yu.D. BuragoV.A. Zalgaller (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Convexity&oldid=15595