Convex surface

A domain (a connected open set) on the boundary of a convex body in the Euclidean space 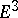. The entire boundary of a convex body is called a complete convex surface. If the body is finite (bounded), the complete convex surface is called closed. If the body is infinite, the complete convex surface is said to be infinite. An infinite convex surface is homeomorphic to a plane or to a circular cylinder. In the latter case it is itself a cylinder. The simplest kind of convex body is a convex polyhedron, i.e. the intersection of a finite number of half-spaces. The surface of a convex polyhedron is composed of convex polygons and is also called a convex polyhedron.

The modern theory of convex surfaces was developed chiefly by Soviet geometers, A.D. Aleksandrov and his school. However, individual results of the theory had been known long before. Thus, the rigidity of a closed convex polyhedron was proved by A.L. Cauchy. H. Liebman and W. Blaschke proved that closed convex surfaces are rigid. H. Minkowski proved the existence of a closed convex surface with given Gaussian curvature. H. Weyl outlined the solution of the problem of the existence of a closed convex surface with a given metric. This solution was perfected by H. Lewy. S.E. Cohn-Vossen proved that regular closed convex surfaces are uniquely definable.

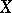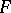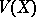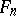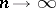To each point of a convex surface naturally corresponds a cone — the limit of the surfaces , as , obtained by a homothety transformation from 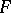with respect to the point 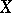with homothety coefficient . This cone is called the tangent cone. Depending on the form of the tangent cone, the points of a convex surface are subdivided into conical, ridge and smooth points. A point of a convex surface is called conical if the tangent cone at this point is not degenerate. If, on the other hand, the tangent cone degenerates to a bihedral angle or a plane, the point is called a ridge point or a smooth point, respectively. Non-smooth points on a convex surface are, in a certain sense, an exception. In fact, the set of ridge points has measure zero, while the set of conical points is at most countable.

The concept of convergence of a series of convex surfaces is defined as follows: A sequence of convex surfaces 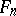converges to a convex surface 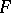if any open set 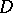intersects or does not intersect at the same time 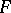and all 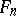if 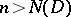. Any convex surface can be represented as a limit of convex polyhedra. Infinite sets of convex surfaces display the important property of compactness, viz. out of any sequence of complete convex surfaces which do not tend to infinity it is always possible to extract a convergent subsequence with as limit a convex surface, which may degenerate (into a twice-covered plane domain, into a straight line, into a half-line, or into a segment).

Any two points of a convex surface can be connected by a rectifiable curve on the surface. The greatest lower bound of the lengths of the curves connecting two given points on a convex surface is said to be the distance between these points on the surface. A curve on a convex surface is called a shortest curve if its length is the smallest of that of the curves on the surface connecting its ends. Any point of a convex surface has a neighbourhood any two points of which can be connected by a shortest curve on the surface. Any two points on a complete convex surface are connected by a shortest curve. A shortest curve on a convex surface has a right and a left semi-tangent at each point. An important property of shortest curves on a convex surface is the non-overlapping property. This means that two shortest curves can be positioned with respect to one another in the following ways only: they have no common points; they have one common point; they have two common points and these points constitute their ends; one shortest curve constitutes a part of the other; or they coincide along a segment, one end of this segment being an end of one shortest curve while the other end is an end of the second. The metric of a convex surface displays the convexity property (cf. Convex metric). The angle between two shortest curves 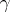and 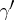at a point 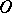is the limit of the angle as 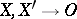. An angle thus defined exists for any two shortest curves issuing from a common point. Due to the non-overlapping of shortest curves, two shortest curves 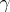and 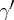issuing from one point subdivide a neighbourhood of this point into two sectors. Let 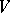be one of these sectors bounded by the shortest curves 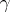and 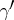. Number in this sector the shortest curves 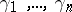, in the sequence of their occurrence on moving from 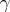to . 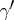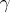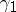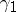Let be the angles enclosed by neighbouring shortest curves and , and 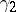, etc. The angle of the sector 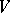is the least upper bound of the sum of the angles 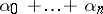over all shortest curves 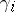inside the sector. The angle of the sector is equal to the angle between the semi-tangents and the shortest curves at the point 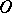on the evolvent of the tangent cone. The sum of the angles of mutually complementary sectors with apex at the point 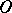does not depend on the specific shortest curves taken and is called the complete angle at the point 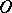. No complete angle at any point of a convex surface is larger than .

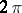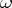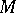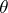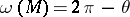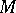The concepts of internal (intrinsic) and external (extrinsic) curvature are defined for a convex surface. The internal curvature is first defined for basic sets — points, open shortest curves and triangles. A triangle is a domain homeomorphic to a circle and bounded by three shortest curves. If is a point and is the complete angle around this point on the surface, . If is an open shortest curve, i.e. a shortest curve with excluded ends, 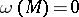. 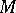If is an open triangle, i.e. a triangle with excluded sides and vertices, 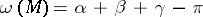, where 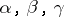are the angles of the triangle. The curvature is further defined for elementary sets, representable in the form of a set-theoretic sum (union) of pairwise non-intersecting basic sets 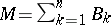. For such sets 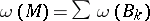. The internal curvature of any closed set is defined as the greatest lower bound of the internal curvatures of the elementary sets containing the closed set. Finally, the internal curvature of any set is defined as the least upper bound of the internal curvatures of the closed sets contained in it. The internal curvature thus defined on a convex surface is a totally-additive function on the ring of Borel sets (cf. Borel set). The external curvature of a set on a convex surface is defined as the area (Lebesgue measure) under the spherical map of this set. It is defined for all Borel sets on a convex surface and is identical with the internal curvature.

A metric 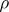on a two-dimensional manifold is called internal if the distance 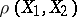between any two points 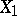and 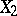of the manifold is equal to the greatest lower bound of the lengths of the curves on this manifold connecting 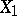and 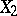. The length of the curve 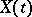, , 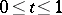connecting the points 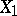and 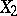is defined as the least upper bound of the sums

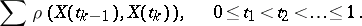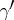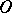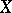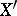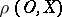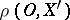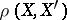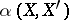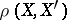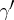Let and be two curves issuing from a point on a manifold with an internal metric. Take points and on these curves and construct the plane triangle with sides , , . The lower limit of the angle of this triangle opposite to the side is called the angle between the curves and at 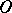. Clearly, this angle always exists. A metric on a manifold is called convex if the sum of the angles of any triangle whose sides are shortest curves is not less than 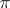. The metric of a convex surface is convex in this sense. One of the principal results in the theory of convex surfaces is the theorem on the realizability of an internal convex metric on some convex surface. Thus, a complete manifold with an internal convex metric is realized by a complete convex surface.

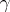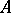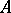The concepts of right and left rotations, which generalize the concept of the integral geodesic curvature, has been introduced for curves on a convex surface. Let be an arbitrary curve without self-intersections on a convex surface, with ends and . A direction on is specified and a sequence of simple geodesic polygonal curves with ends and 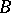, converging to 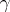and situated in the right semi-neighbourhood of the curve, is constructed. 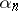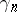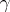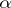Let be the angles of the sectors formed by the links of the polygonal curve on the side of the domain bounded by the and by ; let and 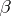be the angles of the sectors formed by the polygonal curve 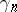and 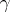at the end points. The limit of 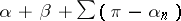as 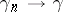is called the right rotation. This limit always exists if the curve 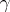has definite directions at the ends, i.e. semi-tangents, and is independent of the sequence in which the polygonal curves were taken. The left rotation is defined in a similar manner. The rotation of a closed curve is defined by approximating it by a closed polygonal curve on the appropriate side. A generalization of the Gauss–Bonnet theorem applies to convex surfaces. In fact, if a closed curve on a convex surface is the boundary of a domain homeomorphic to a disc, the sum of the curvature of the domain and the rotation of the curve bounding the domain on the side of this domain is .

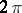An isometric transformation is a deformation of a convex surface during which the surface remains convex and its metric remains unchanged, i.e. distances between points on the surface remain unchanged. An isometric transformation is called trivial if it is reduced to a Euclidean motion of the surface as a whole or to a motion and a mirror reflection. A surface without non-trivial isometric transformations is said to be uniquely defined. Closed convex surfaces and infinite convex surfaces with complete curvature are uniquely defineable. Infinite convex surfaces with complete curvature smaller than 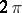may undergo rather arbitrary non-trivial isometric transformations. All convex surfaces have non-trivial local isometric transformations, i.e. each point on a convex surface has a neighbourhood allowing such transformations.

The most important tool in studying isometric transformations of convex surfaces is the glueing theorem. According to this theorem, a complete manifold 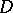consisting of domains that are isometric to a convex surface is itself isometric to a convex surface if the following conditions are met: The boundaries of the domains 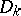have rotations of bounded variation; the segments of the boundary with equal lengths are identified; the sum of the rotations on any of the segments of identified boundaries is non-negative; and the sum of the sector angles at any common point of the boundaries of domains 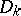does not exceed 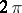. Theorems on the possibility of non-trivial isometric transformation of a convex surface are usually obtained by "glueing" a planar domain to a convex surface, the above conditions being observed.

For general convex surfaces, the concept of an area is introduced for any Borel set; it is introduced at first for the simple sets bounded by shortest curves — geodesic polygons. The polygon is subjected to a fine triangulation 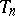so that the sides of the triangles are smaller than 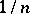. For each triangle of this triangulation one constructs a planar triangle with sides of the same lengths and takes the sum of the areas of such triangles. It is found that, as 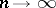, the sum 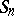tends to a certain limit, irrespective of the manner in which the polygon has been triangulated. This limit is taken as the area of the polygon. In the following step, the areas of closed, open and general Borel sets are determined using the tools of measure theory. The area of a convex surface is a totally-additive function on the ring of Borel sets.

The specific curvature of a convex surface in a domain 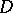is the ratio of the curvature of the domain to its area. If the specific curvature of a convex surface over all domains lies between positive bounds, the surface is smooth and strictly convex. The Gaussian curvature of a convex surface at a given point 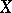is the limit of the specific curvatures of domains 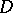as they contract towards 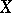. The Gaussian curvature, if it exists, is a continuous function of the points on the surface. If a certain Gaussian curvature exists on a convex surface, it is possible to introduce polar geodesic coordinates on this surface and to represent the line element of the surface in the form

The coefficient is used to determine the Gaussian curvature by the formula:

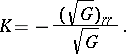A convex surface is called regular if in a neighbourhood of each of its points it can be given by an analytic expression 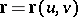, where 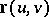is a regular (i.e. a sufficient number of times differentiable) vector-function satisfying the condition 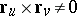. A metric of a convex surface is called regular if it can be specified using a line element

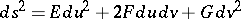and if the coefficients of the form 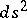are regular functions. A regular convex surface clearly has a regular metric, since

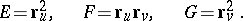The converse proposition is usually false. For instance, a dihedral angle has a regular and even an analytic metric, since it is isometric to a plane, but is not a regular surface. However, if the metric of a convex surface is regular and its Gaussian curvature is positive, the surface is regular. In fact, if the coefficients of the line element are times differentiable (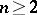), the surface is at least 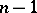times differentiable.

The theory of convex surfaces can also be constructed in spaces of constant curvature. As in the case of Euclidean space, a convex surface is a domain in the boundary of a convex body. Many results of the theory of convex surfaces in spaces of constant curvature are formulated and demonstrated as in the case of Euclidean spaces. However, there may also be essential differences between the respective results. Thus, in the Lobachevskii space, a complete convex surface can be homeomorphic to any connected open set on a sphere.

References

[1]	H. Minkowski, "Volumen und Oberfläche" Math. Ann. , 57 (1903) pp. 447–495
[2]	H. Weyl, "Ueber die Bestimmung einer geschlossenen konvexen Fläche durch ihr Linienelement" Vierteljahrschrift Naturforsch. Gesell. Zurich , 3 : 2 (1916) pp. 40–72
[3]	S.E. Cohn-Vossen, Uspekhi Mat. Nauk , 1 (1936) pp. 33–76
[4]	A.D. Aleksandrov, "Die innere Geometrie der konvexen Flächen" , Akademie Verlag (1955) (Translated from Russian)
[5]	A.V. Pogorelov, "Extrinsic geometry of convex surfaces" , Amer. Math. Soc. (1973) (Translated from Russian)

Comments

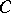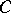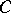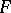Let be a convex body in . A supporting hyperplane at a point in the boundary of is a plane through this point which contains no interior points of . Let be a convex surface bounding 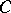. Let 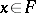; for each supporting plane at to 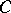consider the half-space not intersecting the interior of (the supporting half-space). The intersection of all supporting half-spaces at is a closed cone. The boundary of this cone is the tangent cone at .

For the notion of rigidity of a convex surface see Deformation and Infinitesimal deformation. The Cohn-Vossen theorem says that if 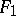is a closed three times continuously-differentiable surface with positive Gaussian curvature, isometric to another such surface 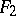, then 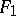is isometric to 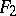or to its mirror image, where congruence of course means that the one is obtained from the other by a Euclidean motion in the ambient space 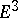, cf. [5], p. 120.

A convex surface 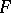is said to be monotypic in a class 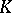of convex surfaces if any surface in 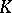isometric to 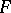is congruent to 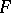. Thus, one has, e.g., the monotypy theorem that two isometric closed convex polyhedra are congruent. Also, any convex surface 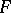(not necessarily a polyhedron) isometric to a closed convex polyhedron is in fact congruent to that polyhedron (S.P. Olovyanishnikov, 1941).

References

[a1]	H. Busemann, "Convex surfaces" , Interscience (1958)
[a2]	R. Schneider, "Boundary structure and curvature of convex bodies" J. Tölke (ed.) J.M. Wills (ed.) , Contributions to geometry , Birkhäuser (1979) pp. 13–59