Convergence in distribution

2020 Mathematics Subject Classification: Primary: 60B10 [MSN][ZBL]

Convergence of a sequence of random variables defined on a certain probability space , to a random variable , defined in the following way: if

(*)

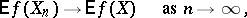for any bounded continuous function . This form of convergence is so called because condition (*) is equivalent to the convergence of the distribution functions to the distribution function at every point at which 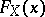is continuous.

Comments

See also Convergence, types of; Distributions, convergence of.

This is special terminology for real-valued random variables for what is generally known as weak convergence of probability measures (same definition as in (*), but with 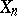, 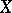taking values in possibly more general spaces).