Controlled stochastic process
A stochastic process whose probabilistic characteristics may be changed (controlled) in the course of its evolution in pursuance of some objective, normally the minimization (maximization) of a functional (the control objective) representing the quality of the control. Various types of controlled processes arise, depending on how the process is specified or on the nature of the control objective. The greatest progress has been made in the theory of controlled jump (or stepwise) Markov processes and controlled diffusion processes when the complete evolution of the process is observed by the controller. A corresponding theory has also been developed in the case of partial observations (incomplete data).
Controlled jump Markov process.
This is a controlled stochastic process with continuous time and piecewise-constant trajectories whose infinitesimal characteristics are influenced by the choice of control. For the construction of such a process the following are usually specified (cf. [1], [2]): 1) a Borel set 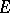 of states; 2) a Borel set
of states; 2) a Borel set 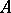 of controls, a set
of controls, a set 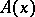 of controls admissible when the process is in state
of controls admissible when the process is in state  , where
, where 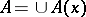 and
and 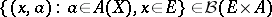 (
(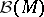 denotes the
denotes the 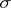 -algebra of Borel subsets of the Borel set
-algebra of Borel subsets of the Borel set 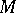 ), and in some cases a measurable selector
), and in some cases a measurable selector 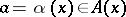 for
for 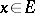 ; 3) a jump measure in the form of a transition function
; 3) a jump measure in the form of a transition function 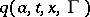 defined for
defined for 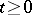 ,
, 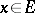 ,
, 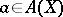 , and
, and 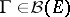 , such that
, such that 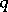 is a Borel function in
is a Borel function in 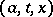 for each
for each 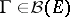 and
and 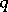 is countably additive in
is countably additive in 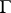 for each
for each  ; moreover
; moreover 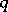 is bounded,
is bounded, 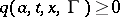 for
for 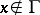 and
and 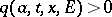 . Roughly speaking,
. Roughly speaking, 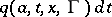 is the probability that the process jumps into the set
is the probability that the process jumps into the set 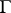 in the time interval
in the time interval  when
when 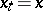 and control action
and control action  is applied.
is applied.
Let 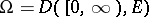 be the space of all piecewise-constant right-continuous functions
be the space of all piecewise-constant right-continuous functions 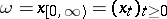 with values in
with values in 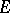 , let
, let 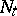 (
(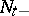 ) be the minimal
) be the minimal 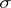 -algebra in
-algebra in  with respect to which the function
with respect to which the function 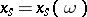 is measurable for
is measurable for 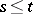 (for
(for 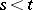 ) and let
) and let 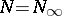 . Any function
. Any function 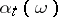 on
on 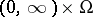 with values
with values 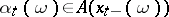 that is progressively measurable relative to the family
that is progressively measurable relative to the family 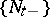 is called a (natural) strategy (or control). From the definition it follows that
is called a (natural) strategy (or control). From the definition it follows that 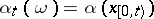 , where
, where 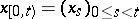 . If
. If 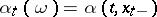 , where
, where 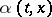 is a Borel function on
is a Borel function on 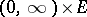 with the property
with the property 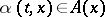 , then
, then 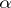 is said to be a Markov strategy or Markov control, and if
is said to be a Markov strategy or Markov control, and if  , it is a stationary strategy or stationary control. The classes of natural, Markov and stationary strategies are denoted by
, it is a stationary strategy or stationary control. The classes of natural, Markov and stationary strategies are denoted by 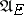 ,
,  and
and 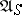 , respectively. In view of the possibility of making a measurable selection from
, respectively. In view of the possibility of making a measurable selection from 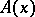 , the class
, the class  (and hence
(and hence 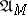 and
and 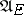 ) is not empty. If
) is not empty. If 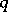 is bounded, then for any
is bounded, then for any 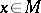 and
and 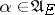 one can construct a unique probability measure
one can construct a unique probability measure 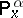 on
on 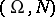 such that
such that 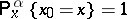 and for any
and for any 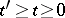 ,
, 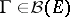 ,
,
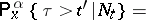 | (1a) |
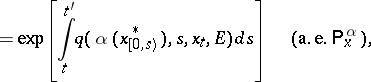 |
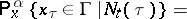 | (1b) |
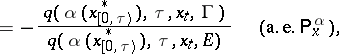 |
where 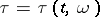 is the first jump time after
is the first jump time after 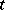 ,
,  is the minimal
is the minimal 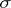 -algebra in
-algebra in  containing
containing  and relative to which
and relative to which  is measurable,
is measurable, 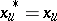 for
for 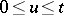 and
and 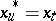 for
for 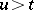 . The stochastic process
. The stochastic process  is a controlled jump Markov process. The control Markov property of a controlled jump Markov process means that from a known "present"
is a controlled jump Markov process. The control Markov property of a controlled jump Markov process means that from a known "present" 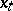 , the "past"
, the "past" 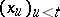 enters in the right-hand side of (1a)–(1b) only through the strategy
enters in the right-hand side of (1a)–(1b) only through the strategy 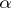 . For an arbitrary strategy
. For an arbitrary strategy 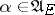 the process
the process 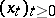 is, in general, not Markovian, but if
is, in general, not Markovian, but if 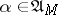 , then one has a Markov process, while if
, then one has a Markov process, while if 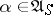 and if
and if 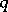 does not depend on
does not depend on 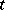 , one has a homogeneous Markov process with jump measure equal to
, one has a homogeneous Markov process with jump measure equal to 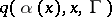 . Control of the process consists of the selection of a strategy from the class of strategies.
. Control of the process consists of the selection of a strategy from the class of strategies.
A typical control problem is the maximization of a functional
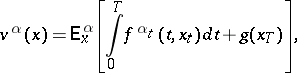 | (2) |
where 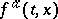 and
and 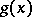 are bounded Borel functions on
are bounded Borel functions on 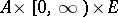 and on
and on 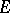 , and
, and  is a fixed number. By defining suitable functions
is a fixed number. By defining suitable functions  and
and 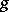 and introducing fictitious states, a wide class of functionals containing terms of the form
and introducing fictitious states, a wide class of functionals containing terms of the form 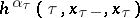 , where
, where  is the moment of jump, and allowing termination of the process, can be reduced to the form (2). By a value function one denotes the function
is the moment of jump, and allowing termination of the process, can be reduced to the form (2). By a value function one denotes the function
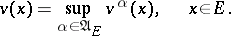 | (3) |
A strategy 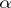 is called
is called  -optimal if
-optimal if 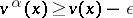 for all
for all 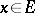 , and
, and 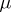 -a.e.
-a.e.  -optimal if this is true for almost-all
-optimal if this is true for almost-all  relative to the measure
relative to the measure 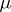 on
on 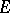 . A
. A  -optimal strategy is called optimal. Now, in the model described above the interval
-optimal strategy is called optimal. Now, in the model described above the interval 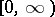 is shortened to
is shortened to 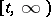 , and the symbols
, and the symbols 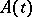 ,
, 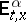 and
and 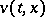 are used in the sense in which
are used in the sense in which 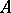 ,
, 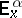 and
and 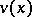 were used before. Considering the jumps of the process as the succession of steps in a controlled discrete-time Markov chain one can establish the existence of a
were used before. Considering the jumps of the process as the succession of steps in a controlled discrete-time Markov chain one can establish the existence of a 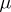 -a.e.
-a.e.  -optimal strategy in the class
-optimal strategy in the class 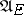 and obtain the measurability of
and obtain the measurability of  in the form:
in the form: 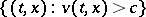 is an analytic set. This allows one to apply the ideas of dynamic programming and to derive the relation
is an analytic set. This allows one to apply the ideas of dynamic programming and to derive the relation
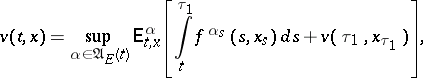 | (4) |
where 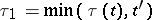 ,
, 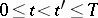 (a variant of Bellman's principle). For
(a variant of Bellman's principle). For 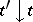 one obtains from (4) and (1a)–(1b) the Bellman equation
one obtains from (4) and (1a)–(1b) the Bellman equation
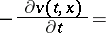 | (5) |
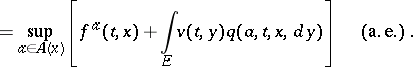 |
The value function 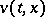 is the only bounded function on
is the only bounded function on 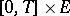 , absolutely continuous in
, absolutely continuous in 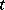 and satisfying (5) and the condition
and satisfying (5) and the condition 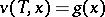 . Equation (5) may be solved by the method of successive approximations. For
. Equation (5) may be solved by the method of successive approximations. For 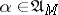 if follows from the Kolmogorov equation for the Markov process
if follows from the Kolmogorov equation for the Markov process 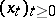 that if the supremum in (5) is attained by a measurable function
that if the supremum in (5) is attained by a measurable function 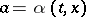 , then the Markov strategy
, then the Markov strategy 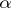 is optimal. In this way the existence of optimal Markov strategies in semi-continuous models (in which
is optimal. In this way the existence of optimal Markov strategies in semi-continuous models (in which 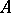 ,
, 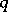 ,
, 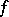 , and
, and  satisfy the compactness and continuity conditions of the definition) is established, in particular for finite models (with finite
satisfy the compactness and continuity conditions of the definition) is established, in particular for finite models (with finite 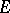 and
and 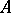 ). In arbitrary Borel models one can conclude the existence of
). In arbitrary Borel models one can conclude the existence of 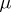 -a.e.
-a.e.  -optimal Markov strategies for any
-optimal Markov strategies for any 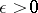 by using a measurable selection theorem (cf. Selection theorems). In countable models one obtains Markov
by using a measurable selection theorem (cf. Selection theorems). In countable models one obtains Markov  -optimal strategies. The results can partly be extended to the case when
-optimal strategies. The results can partly be extended to the case when  and the functions
and the functions 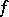 and
and 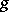 are unbounded, but in general the sufficiency of Markov strategies, i.e. optimality of Markov strategies in the class
are unbounded, but in general the sufficiency of Markov strategies, i.e. optimality of Markov strategies in the class 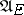 , has not been proved.
, has not been proved.
For homogeneous models, where 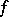 and
and 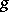 do not depend on
do not depend on 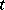 , one considers along with (2) the functionals
, one considers along with (2) the functionals
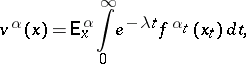 | (6) |
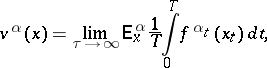 | (7) |
and moreover poses the question of sufficiency for the class 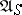 . If
. If 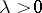 and the Borel function
and the Borel function 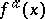 is bounded, then equation (5) for the functional (6) becomes
is bounded, then equation (5) for the functional (6) becomes
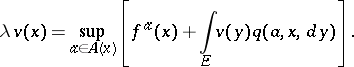 | (8) |
This equation coincides with Bellman's equation for the analogous problem with discrete time and it has a unique bounded solution. If the supremum in (8) is attained for 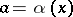 ,
, 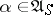 , then
, then 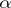 is optimal. The results on the existence of
is optimal. The results on the existence of  -optimal strategies in the class
-optimal strategies in the class 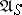 , analogous to those mentioned above, can also be obtained. For the criterion (7) complete results have been obtained only for finite and special forms of ergodic controlled jump Markov processes and similar cases of discrete time: one can choose
, analogous to those mentioned above, can also be obtained. For the criterion (7) complete results have been obtained only for finite and special forms of ergodic controlled jump Markov processes and similar cases of discrete time: one can choose 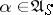 and a function
and a function 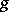 in
in 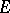 such that
such that 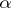 is optimal for the criterion (2) at once for all
is optimal for the criterion (2) at once for all 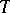 , and hence optimal for the criterion (7).
, and hence optimal for the criterion (7).
Controlled diffusion process.
This is a continuous controlled random process in a 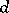 -dimensional Euclidean space
-dimensional Euclidean space 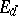 , admitting a stochastic differential with respect to a certain Wiener process which enters exogenously. The theory of controlled diffusion processes arose as a generalization of the theory of controlled deterministic systems represented by equations of the form
, admitting a stochastic differential with respect to a certain Wiener process which enters exogenously. The theory of controlled diffusion processes arose as a generalization of the theory of controlled deterministic systems represented by equations of the form  ,
, 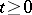 , where
, where 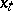 is the state of the system and
is the state of the system and 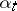 is the control parameter.
is the control parameter.
For a formal description of controlled diffusion processes one uses the language of Itô stochastic differential equations. Let 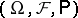 be a complete probability space and let
be a complete probability space and let 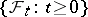 be an increasing family of complete
be an increasing family of complete  -algebras
-algebras 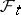 contained in
contained in 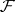 . Let
. Let 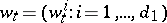 be a
be a 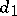 -dimensional Wiener process relative to
-dimensional Wiener process relative to 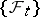 , defined on
, defined on 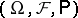 for
for 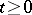 (i.e. a process for which
(i.e. a process for which  is the
is the 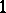 -dimensional continuous standard Wiener process for each
-dimensional continuous standard Wiener process for each 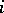 , the processes
, the processes 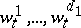 are independent,
are independent, 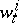 is
is 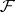 -measurable for each
-measurable for each 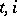 , and for
, and for 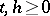 the random variables
the random variables 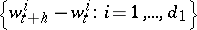 are independent of
are independent of 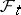 ). Let
). Let 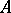 be a separable metric space. For
be a separable metric space. For 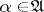 ,
, 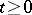 ,
, 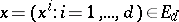 two functions
two functions 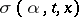 ,
, 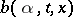 are assumed to be given, where
are assumed to be given, where  is a
is a  -dimensional matrix and
-dimensional matrix and 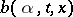 is a
is a 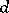 -dimensional vector. Assume that
-dimensional vector. Assume that 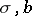 are Borel functions in
are Borel functions in 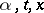 satisfying a Lipschitz condition for
satisfying a Lipschitz condition for  with constants not depending on
with constants not depending on 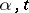 and such that
and such that 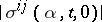 and
and 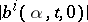 are bounded. An arbitrary process
are bounded. An arbitrary process 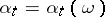 ,
, 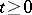 ,
, 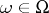 , progressively measurable relative to
, progressively measurable relative to 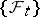 and taking values in
and taking values in 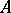 , is called a strategy (or control);
, is called a strategy (or control); 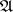 denotes the set of all strategies. For every
denotes the set of all strategies. For every  ,
, 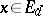 ,
, 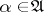 , there exists a unique solution of the Itô stochastic differential equation
, there exists a unique solution of the Itô stochastic differential equation
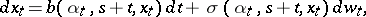 | (9) |
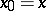 |
(Itô's theorem). This solution, denoted by 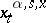 , is called a controlled diffusion process (controlled process of diffusion type); it is controlled by selection of the strategy
, is called a controlled diffusion process (controlled process of diffusion type); it is controlled by selection of the strategy 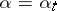 . Besides strategies in
. Besides strategies in 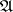 one can consider other classes of strategies. Let
one can consider other classes of strategies. Let  be the space of continuous functions on
be the space of continuous functions on 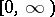 with values in
with values in 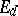 . The semi-axis
. The semi-axis 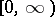 may be interpreted as the set of values of the time
may be interpreted as the set of values of the time 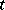 . Elements of
. Elements of 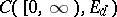 are denoted by
are denoted by 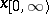 . Further, let
. Further, let 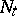 be the smallest
be the smallest 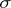 -algebra of subsets of
-algebra of subsets of 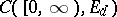 relative to which the coordinate functions
relative to which the coordinate functions 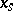 for
for 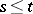 in the space
in the space 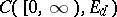 are measurable. A function
are measurable. A function 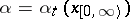 with values in
with values in 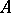 is called a natural strategy, or natural control, admissible at the point
is called a natural strategy, or natural control, admissible at the point 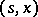 if it is progressively measurable relative to
if it is progressively measurable relative to 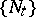 and if for
and if for 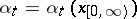 there exists at least one solution of the equation (9) that is progressively measurable relative to
there exists at least one solution of the equation (9) that is progressively measurable relative to 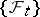 . The set of all natural strategies admissible at
. The set of all natural strategies admissible at 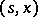 is denoted by
is denoted by 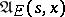 , its subset consisting of all natural strategies of the form
, its subset consisting of all natural strategies of the form 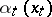 is denoted by
is denoted by 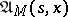 and is called the set of Markov strategies, or Markov controls, admissible at the point
and is called the set of Markov strategies, or Markov controls, admissible at the point 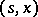 . One can say that a natural strategy defines an equation at the moment of time
. One can say that a natural strategy defines an equation at the moment of time 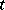 on the basis of the observations of the process
on the basis of the observations of the process 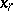 on the time interval
on the time interval 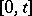 , and that a Markov strategy defines an equation on the basis of observations of the process only at the moment of time
, and that a Markov strategy defines an equation on the basis of observations of the process only at the moment of time 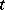 . For
. For 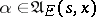 (even for
(even for 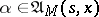 ) the solution of (9) need not be unique. Therefore, for every
) the solution of (9) need not be unique. Therefore, for every 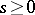 ,
, 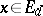 ,
, 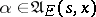 , one arbitrarily fixes some solution of (9) and denotes it by
, one arbitrarily fixes some solution of (9) and denotes it by 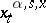 .
.
Then, using the formula 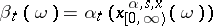 , one defines an imbedding
, one defines an imbedding 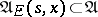 for which
for which  (a. e.).
(a. e.).
The aim of the control is normally to maximize or minimize the expectation of some functional of the trajectory  . A general formulation is as follows. On
. A general formulation is as follows. On 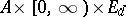 let Borel functions
let Borel functions 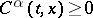 ,
, 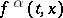 be defined, and let a Borel function
be defined, and let a Borel function 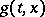 be defined on
be defined on 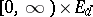 . For
. For 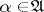 ,
, 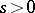 ,
, 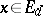 one denotes by
one denotes by 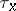 the first exit time of
the first exit time of 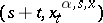 from
from 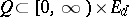 , and puts
, and puts
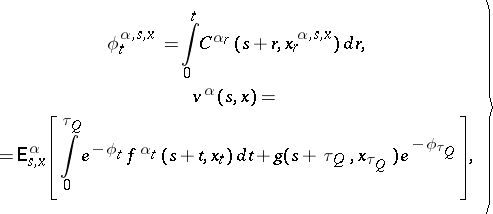 | (10) |
where the indices 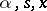 to the expectation sign mean that they should be introduced under the expectation sign as needed. There arises then the problem of determining a strategy
to the expectation sign mean that they should be introduced under the expectation sign as needed. There arises then the problem of determining a strategy  maximizing
maximizing 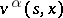 , and of determining a value function
, and of determining a value function
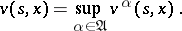 | (11) |
A strategy 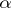 for which
for which  is called
is called  -optimal for the point
-optimal for the point 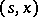 . Optimal means a
. Optimal means a  -optimal strategy. If in (11) the set
-optimal strategy. If in (11) the set 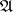 is replaced by
is replaced by 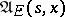 (
(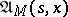 ), then the corresponding least upper bound is denoted by
), then the corresponding least upper bound is denoted by 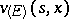 (
(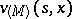 ). Since one has the inclusion
). Since one has the inclusion 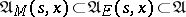 , it follows that
, it follows that 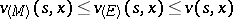 . Under reasonably wide assumptions (cf. [3]) it is known that
. Under reasonably wide assumptions (cf. [3]) it is known that 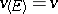 (this is so if, e.g.,
(this is so if, e.g., 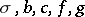 are continuous in
are continuous in 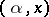 , continuous in
, continuous in  uniformly in
uniformly in 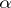 for every
for every 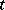 and if
and if 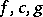 are bounded in absolute value by
are bounded in absolute value by 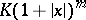 for all
for all  , where
, where 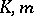 do not depend on
do not depend on 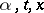 ). The question of the equality
). The question of the equality 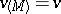 in general situations is still open. A formal application of the ideas of dynamic programming reduces this to the so-called Bellman principle:
in general situations is still open. A formal application of the ideas of dynamic programming reduces this to the so-called Bellman principle:
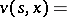 | (12) |
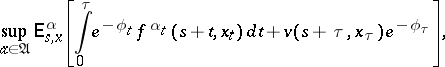 |
where 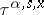 are arbitrarily defined stopping times (cf. Markov moment) not exceeding
are arbitrarily defined stopping times (cf. Markov moment) not exceeding 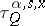 . If in (12) one replaces
. If in (12) one replaces  by
by 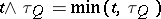 , and applies Itô's formula to
, and applies Itô's formula to 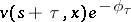 , then after some non-rigorous arguments one arrives at the Bellman equation:
, then after some non-rigorous arguments one arrives at the Bellman equation:
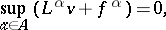 | (13) |
where
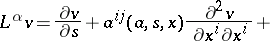 | (14) |
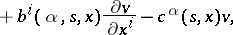 |
and where the indices 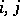 are assumed to be summed from 1 to
are assumed to be summed from 1 to 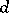 ; the matrix
; the matrix  is defined by
is defined by
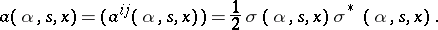 |
Bellman's equation plays a central role in the theory of controlled diffusion processes, since it often turns out that a sufficiently "good" solution of it, equal to 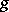 on
on 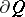 , is the value function, while if
, is the value function, while if 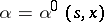 for every
for every 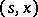 realizes the least upper bound in (13) and
realizes the least upper bound in (13) and 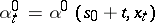 is a Markov strategy admissible at
is a Markov strategy admissible at 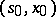 , then the strategy
, then the strategy 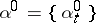 is optimal at the point
is optimal at the point 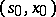 . Thus one can sometimes show that
. Thus one can sometimes show that 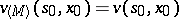 .
.
A rigorous proof of such results meets with serious difficulties, connected with the non-linear character of equation (13), which in general is a non-linear degenerate parabolic equation. The simplest case is that in which (13) is a non-degenerate quasi-linear equation (the matrix  does not depend on
does not depend on 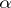 and is uniformly non-degenerate in
and is uniformly non-degenerate in  ). Here, under certain additional restrictions on
). Here, under certain additional restrictions on 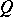 ,
,  ,
,  ,
,  ,
, 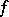 ,
, 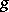 one can make use of results from the theory of quasi-linear parabolic equations to prove the solvability of (13) in Hölder classes of functions and to give a method for constructing
one can make use of results from the theory of quasi-linear parabolic equations to prove the solvability of (13) in Hölder classes of functions and to give a method for constructing  -optimal strategies, based on a solution of (13). An analogous approach can be used (cf. [3]) in the one-dimensional case when
-optimal strategies, based on a solution of (13). An analogous approach can be used (cf. [3]) in the one-dimensional case when 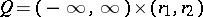 ,
,  ,
, 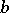 ,
,  ,
, 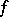 ,
, 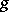 are bounded and do not depend on
are bounded and do not depend on  , and
, and  is uniformly bounded away from zero. In this case (13) reduces to a second-order quasi-linear equation on
is uniformly bounded away from zero. In this case (13) reduces to a second-order quasi-linear equation on 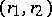 , such that
, such that 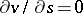 and (13) can be solved for its highest derivative
and (13) can be solved for its highest derivative 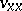 . Methods of the theory of differential equations help in the study of (13) even if
. Methods of the theory of differential equations help in the study of (13) even if 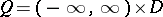 , where
, where 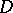 is a two-dimensional domain, and
is a two-dimensional domain, and  ,
, 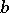 ,
,  ,
, 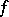 ,
,  do not depend on
do not depend on  (cf. [3]). Here, as in previous cases,
(cf. [3]). Here, as in previous cases,  is allowed to depend on
is allowed to depend on 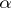 . It is relevant also to mention the case of the Hamilton–Jacobi equation
. It is relevant also to mention the case of the Hamilton–Jacobi equation 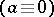 , which may be studied by methods of the theory of differential equations (cf. [5]).
, which may be studied by methods of the theory of differential equations (cf. [5]).
By methods of the theory of stochastic processes one can show that the value function  satisfies equation (13) in more general cases under certain types of smoothness assumptions on
satisfies equation (13) in more general cases under certain types of smoothness assumptions on 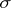 ,
, 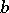 ,
,  ,
, 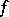 ,
, 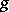 if
if 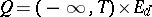 ,
, 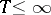 (cf. [3]).
(cf. [3]).
Along with problems of controlled motion, one can also consider optimal stopping of the controlled processes for one or two persons, e.g. maximization over 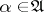 and an arbitrary stopping time
and an arbitrary stopping time  of a value functional of the form:
of a value functional of the form:
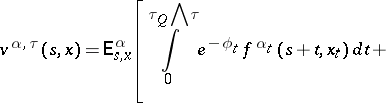 |
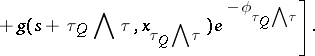 |
Related to the theory of controlled diffusion processes are controlled partially-observable processes and problems of control of stochastic processes, in which the control is realizable by the selection of a measure on 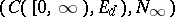 from a given class of measures, corresponding to processes of diffusion type (cf. [3], [4], [6], [7], [8]).
from a given class of measures, corresponding to processes of diffusion type (cf. [3], [4], [6], [7], [8]).
References
| [1] | I.I. [I.I. Gikhman] Gihman, A.V. [A.V. Skorokhod] Skorohod, "Controlled stochastic processes" , Springer (1977) (Translated from Russian) |
| [2] | A.A. Yushkevich, "Controlled jump Markov models" Theory Probab. Appl. , 25 (1980) pp. 244–266 Teor. Veroyatnost. i Primenen. , 25 (1980) pp. 247–270 |
| [3] | N.V. Krylov, "Controlled diffusion processes" , Springer (1980) (Translated from Russian) |
| [4] | W.H. Fleming, R.W. Rishel, "Deterministic and stochastic optimal control" , Springer (1975) |
| [5] | S.N. Kruzhkov, "Generalized solutions of the Hamilton–Jacobi equations of eikonal type. I. Statement of the problem, existence, uniqueness and stability theorems, some properties of the solutions" Mat. Sb. , 98 : 3 (1975) pp. 450–493 (In Russian) |
| [6] | R.S. Liptser, A.N. Shiryaev, "Statistics of random processes" , 1–2 , Springer (1977–1978) (Translated from Russian) |
| [7] | W.M. Wonham, "On the separation theorem of stochastic control" SIAM J. Control , 6 (1968) pp. 312–326 |
| [8] | M.H.A. Davis, "The separation principle in stochastic control via Girsanov solutions" SIAM J. Control and Optimization , 14 (1976) pp. 176–188 |
Comments
The Bellman equations mentioned above (equations (5), (13)) are in this form sometimes called the Bellman–Hamilton–Jacobi equation.
A controlled diffusion process is also defined as a controlled random process, in some Euclidean space, whose measure admits a Radon–Nikodým derivative with respect to a certain Wiener process which is independent of the control.
There are many important topics in the theory of controlled stochastic process other than those mentioned above. Controlled stepwise (jump) processes are of limited interest due to the lack of important applications. The following comments are intended to put the subject in a wider perspective, as well as pointing to some recent technical innovations.
Controlled processes in discrete time.
These are normally specified by a state transition equation
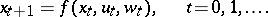 | (a1) |
Here 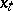 is the state at time
is the state at time 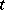 ,
, 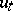 is the control and
is the control and 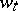 is a given sequence of independent, identically distributed random variables with common distribution function
is a given sequence of independent, identically distributed random variables with common distribution function 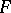 . If the initial state
. If the initial state 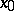 is independent of
is independent of 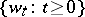 and the control
and the control  is Markovian, i.e.
is Markovian, i.e. 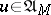 ,
, 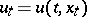 , then the process
, then the process 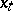 defined by
defined by
is Markovian. The control objective is normally to minimize a cost function such as
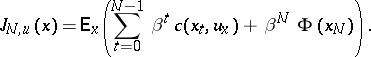 |
The number 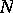 of stages may be finite or infinite;
of stages may be finite or infinite; 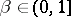 is the discount factor. The one-stage cost with terminal cost
is the discount factor. The one-stage cost with terminal cost 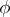 is
is
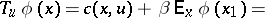 |
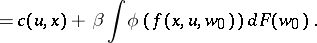 |
Define
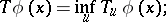 |
then the principle of dynamic programming indicates that
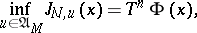 |
where 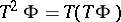 , etc., and that the optimal control
, etc., and that the optimal control 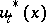 is the value such that
is the value such that
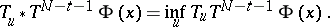 |
In the infinite horizon case (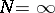 ) one expects that if
) one expects that if 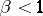 , then
, then
 |
and that 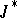 will satisfy Bellman's functional equation
will satisfy Bellman's functional equation
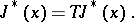 |
The general theory of discrete-time control concerns conditions under which results of the type above can be rigorously substantiated. Generally, contraction (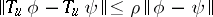 ,
, 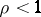 ) or monotonicity (
) or monotonicity (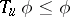 ) conditions are required.
) conditions are required. 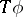 is not necessarily measurable if
is not necessarily measurable if  ,
, 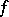 ,
, 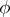 are merely Borel functions. However, if these functions are lower semi-analytic, then
are merely Borel functions. However, if these functions are lower semi-analytic, then 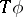 is lower semi-analytic and existence of
is lower semi-analytic and existence of  -optimal universally measurable policies can be proved. [a1], [a2] are excellent references for this theory.
-optimal universally measurable policies can be proved. [a1], [a2] are excellent references for this theory.
Viscosity solutions of the Bellman equations.
Return to the controlled diffusion problem (9), (10) and write the Bellman equation (a1) as
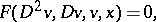 | (a2) |
where 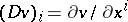 ,
, 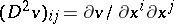 and
and 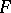 coincides with the left-hand side of (13). As pointed out in the main article, it is a difficult matter to decide in which sense, if any, the value function, defined by (12), satisfies (a2). The concept of viscosity solutions of the Bellman equation, introduced for first-order equations in [a3], provides an answer to this question. A function
coincides with the left-hand side of (13). As pointed out in the main article, it is a difficult matter to decide in which sense, if any, the value function, defined by (12), satisfies (a2). The concept of viscosity solutions of the Bellman equation, introduced for first-order equations in [a3], provides an answer to this question. A function 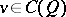 is a viscosity solution of (a2) if for all
is a viscosity solution of (a2) if for all 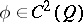 ,
,
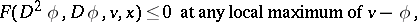 |
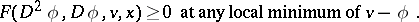 |
Note that any 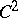 solution of (a2) is a viscosity solution and that if a viscosity solution is
solution of (a2) is a viscosity solution and that if a viscosity solution is  at some point
at some point 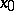 , then (a2) is satisfied at
, then (a2) is satisfied at 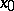 . It is possible to show in great generality that if the value function
. It is possible to show in great generality that if the value function  of (12) is continuous, then it is a viscosity solution of (a1). [a14] can be consulted for a proof of this result, conditions under which
of (12) is continuous, then it is a viscosity solution of (a1). [a14] can be consulted for a proof of this result, conditions under which  is continuous and other results on uniqueness and regularity of viscosity solutions.
is continuous and other results on uniqueness and regularity of viscosity solutions.
A probabilistic approach.
The theory of controlled diffusion is intimately connected with partial differential equations. However the most general results on existence of optimal controls and on stochastic maximum principles (see below) can be obtained by purely probabilistic methods. This is described below for the diffusion model (9) where 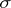 does not depend on
does not depend on  and
and 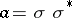 is uniformly positive definite. In this case a weak solution of (9) can be defined for any feedback control
is uniformly positive definite. In this case a weak solution of (9) can be defined for any feedback control 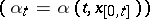 ; denote by
; denote by 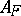 the set of such controls and by
the set of such controls and by 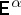 the expectation with respect to the sample space measure for
the expectation with respect to the sample space measure for  when
when 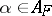 . Suppose that the pay-off (see also Gain function) to be maximized is
. Suppose that the pay-off (see also Gain function) to be maximized is
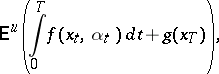 |
where 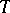 is a fixed time. Define
is a fixed time. Define
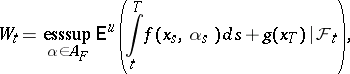 |
where 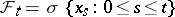 . Let a scalar process
. Let a scalar process 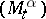 be defined by
be defined by
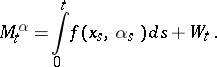 |
Thus, 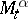 is the maximal expected total pay-off given the control chosen and the evolution of the process up to time
is the maximal expected total pay-off given the control chosen and the evolution of the process up to time 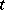 . It is possible to show that
. It is possible to show that 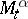 is always a supermartingale (cf. Martingale) and that
is always a supermartingale (cf. Martingale) and that 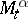 is a martingale if and only if
is a martingale if and only if 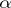 is optimal.
is optimal. 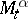 has the Doob–Meyer decomposition
has the Doob–Meyer decomposition 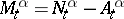 , where
, where 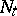 is a martingale and
is a martingale and 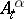 is a continuous increasing process. Thus
is a continuous increasing process. Thus 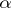 is optimal if and only if
is optimal if and only if 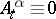 . By the martingale representation theorem (cf. Martingale),
. By the martingale representation theorem (cf. Martingale), 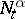 can always be written in the form
can always be written in the form
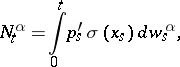 |
where 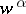 is the Wiener process appearing in the weak solution of (9) with control
is the Wiener process appearing in the weak solution of (9) with control 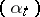 . It is easily shown that
. It is easily shown that 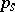 does not depend on
does not depend on 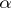 and that the relation between
and that the relation between 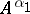 and
and 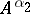 for
for  is
is
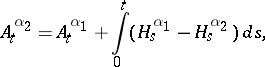 |
where
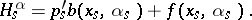 |
This immediately gives a maximum principle: if 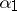 is optimal, then
is optimal, then 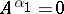 ; but
; but 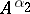 is increasing, so it must be the case that
is increasing, so it must be the case that 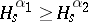 a.e., which implies that
a.e., which implies that
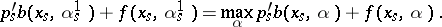 | (a3) |
One also gets an existence theorem: Since 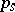 is the same for all controls one can construct an optimal control
is the same for all controls one can construct an optimal control 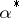 by taking
by taking
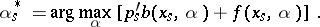 |
Similar techniques can be applied to very general classes of controlled stochastic differential systems (not just controlled diffusion) and to optimal stopping and impulse control problems (see below). General references are [a5], [a6]. Some of this theory has also been developed using methods of non-standard analysis [a7].
Stochastic maximum principle.
The necessary condition (a3) is not as it stands a true maximum principle because the "adjoint variable" 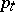 is only implicitly characterized. It is shown in [a8] and elsewhere that under wide conditions
is only implicitly characterized. It is shown in [a8] and elsewhere that under wide conditions 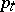 is given by
is given by
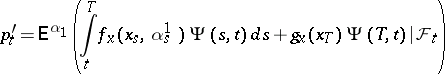 |
where 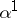 is an optimal control and
is an optimal control and 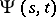 is the fundamental solution of the linearized or derivative system corresponding to (9) with control
is the fundamental solution of the linearized or derivative system corresponding to (9) with control 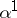 , i.e. it satisfies
, i.e. it satisfies
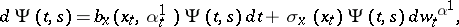 |
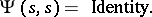 |
This gives the stochastic maximum principle in a form which is directly analogous to the Pontryagin maximum principle of deterministic optimal control theory.
Impulse control.
In many important applications, control is not exercized continuously, but rather a sequence of "interventions" is made at isolated instants of time. The theory of impulse control is a mathematical formulation of this kind of problem. Let 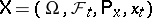 be a homogeneous Markov process on a state space
be a homogeneous Markov process on a state space 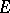 , where
, where 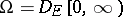 (the set of right-continuous
(the set of right-continuous 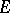 -valued function having limits from the left). Let
-valued function having limits from the left). Let 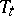 be the corresponding semi-group:
be the corresponding semi-group: 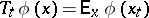 . Informally, a controlled process
. Informally, a controlled process 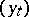 is defined as follows. A strategy
is defined as follows. A strategy 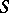 is a sequence
is a sequence 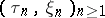 of random times
of random times 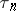 and states
and states 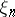 , with
, with 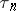 strictly increasing.
strictly increasing. 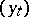 starts at some fixed point
starts at some fixed point  and follows a realization of
and follows a realization of 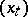 up to time
up to time 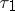 . At
. At 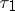 the position of
the position of 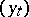 is moved to
is moved to 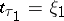 , then follows a realization of
, then follows a realization of 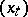 starting at
starting at 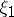 up to time
up to time 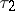 ; etc. A filtered probability space
; etc. A filtered probability space 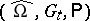 carrying
carrying 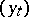 is constructed in such a way that
is constructed in such a way that 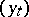 is adapted to
is adapted to 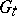 (cf. Optional random process) and for each
(cf. Optional random process) and for each 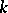 ,
, 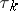 is a
is a  stopping time and
stopping time and 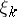 is
is 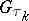 -measurable. It is convenient to formulate the optimization problem in terms of minimizing a cost function
-measurable. It is convenient to formulate the optimization problem in terms of minimizing a cost function 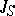 , which generally takes the form
, which generally takes the form
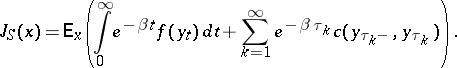 |
Suppose that 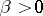 and
and 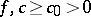 ; this rules out the strategies having more than a finite number of interventions in bounded time intervals. The value function is
; this rules out the strategies having more than a finite number of interventions in bounded time intervals. The value function is
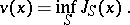 |
Define the operator 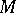 by
by
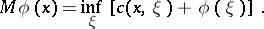 |
When 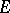 is compact and
is compact and 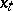 is a Feller process it is possible to show [a9] that
is a Feller process it is possible to show [a9] that  is continuous and that
is continuous and that  is the largest continuous function satisfying
is the largest continuous function satisfying
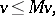 | (a4) |
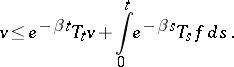 | (a5) |
The optimal strategy 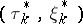 is:
is:
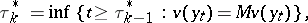 |
 |
Thus, the state space  divides into a continuation set, where
divides into a continuation set, where 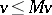 , and an intervention set, where
, and an intervention set, where 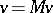 . Further,
. Further,  is the unique solution of
is the unique solution of
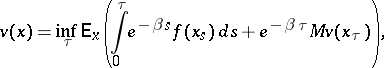 | (a6) |
where the infimum is taken over the set of 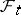 stopping times
stopping times  . This shows the close connection between impulse control and optimal stopping: (a6) is an optimal stopping problem for the process
. This shows the close connection between impulse control and optimal stopping: (a6) is an optimal stopping problem for the process 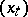 with implicit obstacle
with implicit obstacle 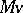 . Similar results are obtained for right processes in [a6], [a10]; the measurability properties here are more delicate. There is also well-developed analytic theory of impulse control. Assuming
. Similar results are obtained for right processes in [a6], [a10]; the measurability properties here are more delicate. There is also well-developed analytic theory of impulse control. Assuming 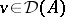 , where
, where 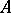 is the differential generator of
is the differential generator of 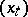 , one obtains from (a5)
, one obtains from (a5)
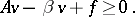 | (a7) |
Further, equality holds in at least one of (a4), (a7) at each  , i.e.
, i.e.
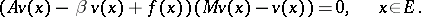 | (a8) |
Equations (a4), (a7), (a8) characterize  and have been extensively studied for diffusion processes (i.e. when
and have been extensively studied for diffusion processes (i.e. when 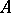 is a second-order differential operator) using the method of quasi-variational inequalities [a11]. Existence and regularity properties are obtained.
is a second-order differential operator) using the method of quasi-variational inequalities [a11]. Existence and regularity properties are obtained.
Control of applied non-diffusion models.
Many applied problems in operations research — for example in queueing systems or inventory control — involve optimization of non-diffusion stochastic models. These are generalizations of the jump process described in the main article allowing for non-constant trajectories between jumps and for various sorts of boundary behaviour. There have been various attempts to create a unified theory for such problems: piecewise-deterministic Markov processes [a12], Markov decision drift processes [a13], [a14]. Both continuous and impulse control are studied, as well as discretization methods and computational techniques.
Control of partially-observed processes.
This subject is still far from completely understood, despite important recent advances. It is closely related to the theory of non-linear filtering. Consider a controlled diffusion as in (9), where control must be based on observations of a scalar process 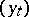 given by
given by
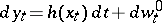 | (a9) |
(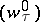 is another independent Wiener process and
is another independent Wiener process and 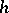 is, say, bounded), with a pay-off functional of the form
is, say, bounded), with a pay-off functional of the form
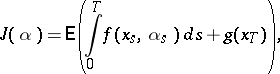 |
is to be maximized. This problem can be formulated in the following way. Let 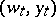 be independent Wiener processes on some probability space
be independent Wiener processes on some probability space 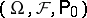 and let
and let 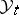 be the natural filtration of
be the natural filtration of 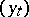 . The admissible controls
. The admissible controls 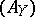 are all
are all 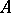 -valued processes
-valued processes 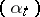 adapted to
adapted to 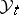 . Under standard conditions (9) has a unique strong solution for
. Under standard conditions (9) has a unique strong solution for 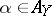 . Now define a measure
. Now define a measure 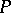 on
on 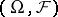 by
by
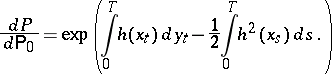 |
By Girsanov's theorem, 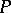 is a probability measure and
is a probability measure and 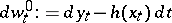 is Wiener process under measure
is Wiener process under measure 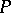 . Thus
. Thus 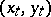 satisfy (9), (a9) on
satisfy (9), (a9) on 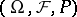 . For any function
. For any function 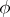 , put
, put 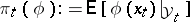 . According to the Kallianpur–Striebel formula,
. According to the Kallianpur–Striebel formula, 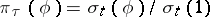 where 1 denotes the function
where 1 denotes the function 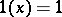 and
and
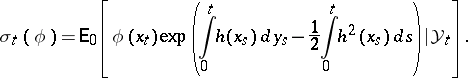 |
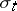 can be thought of as a non-normalized conditional distribution of
can be thought of as a non-normalized conditional distribution of 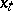 given
given 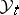 ; it satisfies the Zakai equation
; it satisfies the Zakai equation
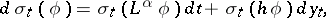 | (a10) |
where 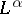 is given by (14) with
is given by (14) with 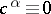 . It follows from the properties of conditional mathematical expectation that
. It follows from the properties of conditional mathematical expectation that  can be expressed in the form
can be expressed in the form
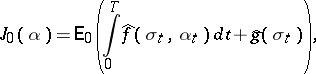 |
where 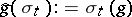 and
and 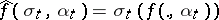 . This shows that the partially-observed problem (9), (a9) is equivalent to a problem (a10),
. This shows that the partially-observed problem (9), (a9) is equivalent to a problem (a10),
with complete observations on the probability space 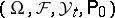 where the controlled process is the measure-valued diffusion
where the controlled process is the measure-valued diffusion 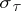 . The question of existence of optimal controls has been extensively studied. It seems that optimal controls do exist, but only if some form of randomization is introduced; see [a7], [a15], [a16]. In addition, maximum principles have been obtained [a17], [a18] and some preliminary study of the Bellman equation undertaken [a19].
. The question of existence of optimal controls has been extensively studied. It seems that optimal controls do exist, but only if some form of randomization is introduced; see [a7], [a15], [a16]. In addition, maximum principles have been obtained [a17], [a18] and some preliminary study of the Bellman equation undertaken [a19].
References
| [a1] | D.P. Bertsekas, S.E. Shreve, "Stochastic optimal control: the discrete-time case" , Acad. Press (1978) |
| [a2] | E.B. Dynkin, A.A. Yushkevich, "Controlled Markov processes" , Springer (1979) |
| [a3] | M.G. Crandall, P.L. Lions, "Viscosity solutions of Hamilton–Jacobi equations" Trans. Amer. Math. Soc. , 277 (1983) pp. 1–42 |
| [a4a] | P.L. Lions, "Optimal control of diffusion processes and Hamilton–Jacobi–Bellman equations Part I" Comm. Partial Differential Eq. , 8 (1983) pp. 1101–1134 |
| [a4b] | P.L. Lions, "Optimal control of diffusion processes and Hamilton–Jacobi–Bellman equations Part II" Comm. Partial Differential Eq. , 8 (1983) pp. 1229–1276 |
| [a5] | R.J. Elliott, "Stochastic calculus and applications" , Springer (1982) |
| [a6] | N. El Karoui, "Les aspèctes probabilistes du contrôle stochastique" , Lect. notes in math. , 876 , Springer (1980) |
| [a7] | S. Albeverio, J.E. Fenstad, R. Høegh-Krohn, T. Lindstrøm, "Nonstandard methods in stochastic analysis and mathematical physics" , Acad. Press (1986) |
| [a8] | U.G. Hausmann, "A stochastic maximum principle for optimal control of diffusions" , Pitman (1986) |
| [a9] | M. Robin, "Contrôle impulsionel des processus de Markov" , Univ. Paris IX (1978) (Thèse d'Etat) |
| [a10] | J.P. Lepeltier, B. Marchal, "Théorie générale du contrôle impulsionnel Markovien" SIAM. J. Control and Optimization , 22 (1984) pp. 645–665 |
| [a11] | A. Bensoussan, J.L. Lions, "Impulse control and quasi-variational inequalities" , Gauthier-Villars (1984) |
| [a12] | M.H.A. Davis, "Piecewise-deterministic Markov processes: a general class of non-diffusion stochastic models" J. Royal Statist. Soc. (B) , 46 (1984) pp. 353–388 |
| [a13] | F.A. van der Duyn Schouten, "Markov decision drift processes" , CWI , Amsterdam (1983) |
| [a14] | A.A. Yushkevich, "Continuous-time Markov decision processes with intervention" Stochastics , 9 (1983) pp. 235–274 |
| [a15] | W.H. Fleming, E. Paradoux, "Optimal control for partially-observed diffusions" SIAM J. Control and Optimization , 20 (1982) pp. 261–285 |
| [a16] | V.S. Borkar, "Existence of optimal controls for partially-observed diffusions" Stochastics , 11 (1983) pp. 103–141 |
| [a17] | A. Bensoussan, "Maximum principle and dynamic programming approaches of the optimal control of partially-observed diffusions" Stochastics , 9 (1983) pp. 169–222 |
| [a18] | U.G. Haussmann, "The maximum principle for optimal control of diffusions with partial information" SIAM J. Control and Optimization , 25 (1987) pp. 341–361 |
| [a19] | V.E. Beneš, I. Karatzas, "Filtering of diffusions controlled through their conditional measures" Stochastics , 13 (1984) pp. 1–23 |
| [a20] | D.P. Bertsekas, "Dynamic programming and stochastic control" , Acad. Press (1976) |
| [a21] | H.J. Kushner, "Stochastic stability and control" , Acad. Press (1967) |
| [a22] | C. Striebel, "Optimal control of discrete time stochastic systems" , Lect. notes in econom. and math. systems , 110 , Springer (1975) |
| [a23] | P.L. Lions, "On the Hamilton–Jacobi–Bellmann equations" Acta Appl. Math. , 1 (1983) pp. 17–41 |
| [a24] | M. Robin, "Long-term average cost control problems for continuous time Markov processes. A survey" Acta Appl. Math. , 1 (1983) pp. 281–299 |
Controlled stochastic process. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Controlled_stochastic_process&oldid=50983