Continuous functions, space of

A normed space of bounded continuous functions on a topological space with the norm . Convergence of a sequence in means uniform convergence. The space is a commutative Banach algebra with a unit element. If is compact, then every continuous function is bounded, consequently, is the space of all continuous functions on .

When 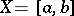is a closed interval of real numbers, 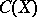is denoted by . According to the Weierstrass theorem on the approximation of continuous functions, the set of all non-negative integral powers forms a complete system in 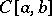. (This means that the set of linear combinations of these powers, that is, polynomials, is everywhere-dense in 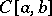.) Consequently, is separable; it also has a basis, for example, the Faber–Schauder system of functions forms a basis in . A criterion for compactness in is given by the corresponding theorem of Arzelá: For a certain family of functions 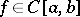to be relatively compact in it is necessary and sufficient that the family is uniformly bounded and equicontinuous. This theorem generalizes to the case of the metric space 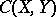of continuous mappings from one metric compactum 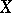to another 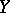. For the compactness of a closed subset of 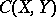it is necessary and sufficient that the mappings in are equicontinuous. The distance between two mappings 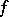and in 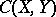is given by

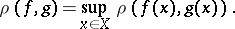References

[1]	P.S. Aleksandrov, "Einführung in die Mengenlehre und die allgemeine Topologie" , Deutsch. Verlag Wissenschaft. (1984) (Translated from Russian)
[2]	A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian)

Comments

The Arzelá theorem is also known as the Ascoli–Arzelá theorem in the setting of functions on a compact metric space . A sequence of functions 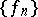in 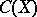is relatively compact (i.e. the closure of the set 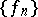is compact), if the sequence is uniformly bounded (also called equibounded), i.e. , and is equicontinuous (in ), i.e.

References

[a1]	N. Bourbaki, "Elements of mathematics. General topology" , Addison-Wesley (1966) pp. Chapt. 10 (Translated from French)
[a2]	K. Yosida, "Functional analysis" , Springer (1978) pp. 68ff
[a3]	B.Z. Vulikh, "Introduction to functional analysis" , Pergamon (1963)