Confocal conics
co-focal curves
Curves of the second order with common foci. If $F$ and $F_1$ are two given points in the plane, then through every point of the plane there are one ellipse and one hyperbola that have $F$ and $F_1$ as their foci (Fig. a).
Every ellipse is orthogonal to every hyperbola confocal with it, that is, they intersect (in four points) at right angles. In a suitable coordinate system, all the confocal ellipses and hyperbolas can be given by the equation
$$\frac{x^2}{\lambda}+\frac{y^2}{\lambda-c^2}=1,\label{*}\tag{*}$$
where $c$ is the distance of the foci from the coordinate origin and $\lambda$ is a variable parameter. If $\lambda>c^2$, this equation defines an ellipse, and if $0<\lambda<c^2$, it defines a hyperbola (if $\lambda<0$, it is an imaginary curve of the second order). If one of the foci tends to infinity, then in the limit one obtains two families of confocal parabolas (Fig. b).
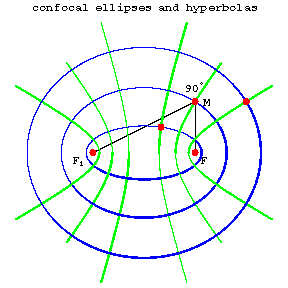
Figure: c024710a
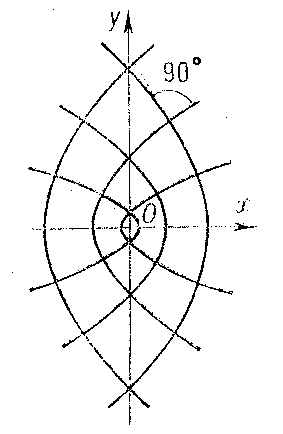
Figure: c024710b
Any two parabolas from different families are also orthogonal to one another. Confocal ellipses and hyperbolas can be used to introduce the system of elliptic coordinates in the plane as follows. If $M(x,y)$ is any point of the plane, then by substituting its coordinates $x$ and $y$ into \eqref{*}, one obtains a quadratic equation for $\lambda$; its roots $\lambda_1,\lambda_2$ are the elliptic coordinates of $M$. The confocal ellipses and hyperbolas themselves form the coordinate net of this coordinate system, that is, they are defined by the equations $\lambda_1=\text{const}$ and $\lambda_2=\text{const}$.
References
| [a1] | D.J. Struik, "Lectures on analytic and projective geometry" , Addison-Wesley (1953) pp. 157–160 |
Confocal conics. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Confocal_conics&oldid=53380