Calderón-type reproducing formula

A formula giving an integral representation of the identity operator and having a number of realizations depending on the initial setting. Historically, it is usually connected with the paper [a1] by A.P. Calderón (1964), but its basic idea was known before.

The Calderón reproducing formula is widely used in the theory of continuous wavelet transforms [a2] (cf. also Wavelet analysis).

Given a function $f \in L ^ { 2 } ( \mathbf{R} ^ { n } )$ and sufficiently nice radial functions $u$ and $v$, the Calderón reproducing formula reads:

\begin{equation} \tag{a1} \int _ { 0 } ^ { \infty } \frac { f * u _ { t } * v _ { t } } { t } d t = c _ { u , v }\, f, \end{equation}

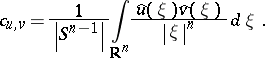Here, $u _ { t } ( x ) = t ^ { - n } u ( x / t )$, $v _ { t } ( x ) = t ^ { - n } v ( x / t )$, "*" is a convolution operator, $| S ^ { n - 1 } |$ is the area of the unit sphere $S ^ { n - 1 }$ in ${\bf R} ^ { n }$, and $\widehat{u}$ and $\hat{v} $ designate the Fourier transforms of $u$ and $v$ (cf. also Fourier transform). The convolution $( W _ { u } f ) ( x , t ) = ( f ^ { * } u _ { t } ) ( x )$ is called the continuous wavelet transform, $u ( x )$ is called an analyzing wavelet and $v ( x )$ is called a reconstructing wavelet. The pair $( u , v )$ is called admissible if $0 \neq \mathfrak { c } _ { u , v} < \infty$. The integral $\int _ { 0 } ^ { \infty }$ in (a1) is treated as the $L^{2}$-limit of the corresponding truncated integral $\int _ { \epsilon } ^ { \rho }$ as $\epsilon \rightarrow 0$ and $\rho \rightarrow \infty$.

A generalization of (a1) has the form [a3]:

\begin{equation} \tag{a2} \int _ { 0 } ^ { \infty } \frac { f ^ {*} \mu _ { t } } { t } d t \equiv \operatorname { lim } _ { \epsilon \rightarrow 0 , \rho \rightarrow \infty } \int _ { \epsilon } ^ { \rho } \frac { f ^ {*} \mu _ { t } } { t } d t = c _ { \mu } \,f, \end{equation}

where $\mu$ is a suitable radial Borel measure, $\mu _ { t }$ stands for the dilation of $\mu$, and the limit is interpreted in the $L ^ { p }$-norm and in the "almost everywhere" sense. If $\mu$ is not radial, then the left-hand side of (a2) is a sum $c _ { \mu } f + T _ { \mu } f$, where $T _ { \mu } f$ is a certain Calderón–Zygmund singular integral (cf. also Singular integral; [a4]). At many occurrences one can write

\begin{equation*} \mu _ { t } = t \frac { \partial } { \partial t } k _ { t }, \end{equation*}

provided that $k _ { t } ^ { * } f$ is an approximate identity (cf. also Involution algebra). A formal integral $\int _ { 0 } ^ { \infty } \mu _ { t } d t / t$ (cf. (a2)) can be regarded as an integral representation of the delta-function. More general representations, corresponding to inhomogeneous dilations on homogeneous groups, are given in [a5].

Calderón-type reproducing formulas (and the relevant continuous wavelet transforms) can be obtained starting out from analytic families of operators, involving the identity operator $I$. If $\{ A ^ { \alpha } \}$ is such a family, $A ^ { 0 } = I$, and $\operatorname{a.c.}A ^ { \alpha } f$ is an analytic continuation of $A ^ { \alpha } f$ in the $\alpha$-variable, then the equality $( \text { a.c. } A ^ { \alpha } f ) _ { \alpha = 0 } = f$ can be written as a Calderón-type reproducing formula provided that a suitable notion of analytic continuation is employed. For this purpose one can use a generalization of the method of A. Marchaud, described in [a6], Sec. 10.7. In accordance with the generalized Marchaud method, (a2) can be related to the analytic family of Riesz potentials $I ^ { \alpha } f$ (cf. also Riesz potential) defined by $\widehat { ( I ^ { \alpha } f ) } ( \xi ) = | \xi | ^ { - \alpha } \hat { f } ( \xi )$, and possessing a wavelet-type representation of the form

\begin{equation*} ( I ^ { \alpha } f ) ( x ) = c _ { \mu , \alpha } \int _ { 0 } ^ { \infty } ( f ^ { * } \mu _ { t } ) ( x ) t ^ { \alpha - 1 } d t, \end{equation*}

cf. [a6], Sec. 17. An analogue of (a2) for the unit sphere $S ^ { 2 }$, corresponding to the spherical Riesz potentials, reads [a6], Sec. 34:

\begin{equation*} \int _ { 0 } ^ { \infty } ( V _ { g } f ) ( \theta , t ) \frac { d t } { t } = c _ { g } \,f, \end{equation*}

\begin{equation*} c _g = \int _ { 0 } ^ { \infty } g ( t ) \operatorname { log } \frac { 1 } { t } d t, \end{equation*}

where $\theta \in S ^ { 2 }$ and

\begin{equation*} ( V _ { g } f ) ( \theta , t ) = ( 2 \pi t ) ^ { - 1 } \int _ { S ^ { 2 } } f ( \sigma ) g \left( \frac { 1 - \theta . \sigma } { t } \right) d \sigma \end{equation*}

is a spherical convolution, which can be regarded as a "spherical wavelet transform" .

Further generalizations of (a2) can be associated with integral representations of the unit mass uniformly distributed on a sufficiently smooth surface. In such a case, the function $f$ on the right-hand side of (a2) should be replaced by the relevant Radon transform. Some examples related to $k$-plane transforms in ${\bf R} ^ { n }$ and spherical Radon transforms in $S ^ { n }$ can be found in [a7].

Formula (a2) can be extended to non-radial measures $\mu$ as follows. Let $\operatorname{SO} ( n )$ be the special orthogonal group of rotations of ${\bf R} ^ { n }$. For $\gamma \in \operatorname{SO} ( n )$ and $t > 0$, let $\mu_{ \gamma , t}$ be the rotated and dilated version of $\mu$. A natural generalization of (a2) reads [a3]:

\begin{equation} \tag{a3} \int _ { \operatorname{SO} ( n ) } d \gamma \int _ { 0 } ^ { \infty } \frac { f ^ { * } \mu _ { \gamma , t } } { t } d t = c _ { \mu } f. \end{equation}

A remarkable feature of this formula is that, with a suitable choice of $\mu$, it gives rise to a series of explicit inversion formulas for a number of important transforms in integral geometry [a3]. For example, assume that $x \in \mathbf{R} ^ { n }$ is represented as $x = ( x ^ { \prime } , x ^ { \prime \prime } )$, $x ^ { \prime } = ( x _ { 1 } , \dots , x _ { k } )$, $x ^ { \prime \prime } = ( x _ { k+1}, \dots , x _ { n } )$, $1 \leq k \leq n - 1$, and $\mu \equiv \mu ( x )$ has the form $\mu ( x ) = m ( x ^ { \prime } ) \times \lambda ( x ^ { \prime \prime } )$, where $m ( x ^ { \prime } )$ is the Lebesgue measure on $\mathbf{R} ^ { k }$ and $\lambda ( x ^ { \prime \prime } )$ is a suitable reconstructing measure on the $x ^ { \prime \prime }$-plane. Then (a3) can be rewritten as an inversion formula for the $k$-plane transform, which assigns to $f$ a collection of integrals of $f$ over all $k$-dimensional planes in ${\bf R} ^ { n }$. The idea of such an application of the Calderón reproducing formula is due to M. Holschneider [a8], Sec. 12, who considered the case $n = 2$. Another choice of $\mu$ in (a3) leads to an explicit inversion of windowed X-ray transforms (cf. also X-ray transform), defined by

\begin{equation} \tag{a4} ( X _ { \nu } f ) ( x , y ) = \int _ { - \infty } ^ { \infty } f ( x + t y ) d \nu ( t ), \end{equation}

\begin{equation*} x , y \in \mathbf{R} ^ { n } \end{equation*}

with a finite Borel measure $\nu$. The transform (a4) with $d \nu ( t ) = g ( t ) d t$, where $g$ is a "nice" compactly supported function (a window function), was introduced by G.A. Kaizer and R.F. Streater [a9] in connection with applications in physics.

The Calderón reproducing formula admits various discrete versions, which serve as natural analogues of atomic decompositions and play an important role in the study of function spaces [a10].

References

[a1]	A.P. Calderón, "Intermediate spaces and interpolation, the complex method" Studia Math. , 24 (1964) pp. 113–190
[a2]	Y. Meyer, "Wavelets and operators" , Cambridge Univ. Press (1992)
[a3]	B. Rubin, "The Calderón reproducing formula, windowed X-ray transforms and Radon transforms in $L ^ { p }$-spaces" J. Fourier Anal. Appl. , 4 (1998) pp. 175–197
[a4]	D. Ryabogin, B. Rubin, "Singular integral operators generated by wavelet transforms" Integral Eq. Operator Th. (in press},)
[a5]	G.B. Folland, E.M. Stein, "Hardy spaces on homogeneous groups" , Princeton Univ. Press (1982)
[a6]	B. Rubin, "Fractional integrals and potentials" , Addison-Wesley (1996)
[a7]	B. Rubin, "Fractional calculus and wavelet transforms in integral geometry" Fractional Calculus and Applied Analysis , 2 (1998) pp. 193–219
[a8]	M. Holschneider, "Wavelets: an analysis tool" , Clarendon Press (1995)
[a9]	G.A. Kaiser, R.F. Streater, "Windowed Radon transforms, analytic signals, and wave equation" C.K. Chui (ed.) , Wavelets: A Tutorial in Theory and Applications , Acad. Press (1992) pp. 399–441
[a10]	M. Frazier, B. Jawerth, G. Weiss, "Littlewood–Paley theory and the study of function spaces" , CBMS Reg. Conf. Ser. Math. , 79 , Amer. Math. Soc. (1991)