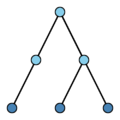
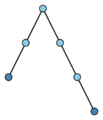
Binary tree
2020 Mathematics Subject Classification: Primary: 05C05 [MSN][ZBL]
A (planar) rooted tree for which every node has a left child, a right child, neither, or both. Three examples are:
These three are all different.
The number of binary trees with $n$ nodes, $p$ left children, $q$ right children ($p+q=n-1$) is
$$\frac{1}{n}\binom{n}{p}\binom{n}{p+1} = \frac{1}{n}\binom{n}{p}\binom{n}{q}.$$
The numbers $\frac{1}{n}\binom{n}{p}\binom{n}{p+1}$ are called Runyon numbers or Narayana numbers (OEIS sequence A001263).
A complete binary tree is one in which every node has both left and right children or is a leaf (i.e., has no children). E.g., there are two complete binary trees with five nodes:
A complete binary tree has an odd number of nodes, say $2k+1$, and then the number of leaves is $k+1$. Label the $k+1$ leaves from left to right with symbols $x_1,\dotsc,x_{k+1}$. Then the various complete binary trees with their $k+1$ leaves labelled in this order precisely correspond to all the different ways of putting brackets in the word $x_1\cdots x_{k+1}$, each way corresponding to a computation of the product by successive multiplications of precisely two factors each time. The number of ways of doing this, and hence the number of binary trees with $k+1$ nodes, is the Catalan number
$$\frac{1}{k+1}\binom{2k}{k},k=1,2,\dotsc$$
which is OEIS sequence A000108.
The problem of all such bracketings of a product (of numbers) was considered by E. Catalan in 1838 [a1].
The correspondence between complete binary trees and (complete) bracketings gives a bijection between complete binary trees with leaves labelled with elements from a set $X$ and the free magma on $X$.
References
- [a1] E. Catalan, "Note sur une équation aux différences finies" J. Math. Pures Appl. , 3 (1838) pp. 508–516
- [a2] L. Comtet, "Advanced combinatorics" , Reidel (1974) Zbl 0283.05001
- [a3] I.M. Gessel, R.P. Stanley, "Algebraic enumeration" R.L. Graham (ed.) M. Grötschel (ed.) L. Lovacz (ed.) , Handbook of Combinatorics , II , Elsevier (1995) pp. 1021–1062
- [a4] R.P. Stanley, "Enumerative combinatorics" , Wadsworth and Brooks/Cole (1986)
Binary tree. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Binary_tree&oldid=54373