Bazilevich functions

Let $A$ be the class of functions $f ( z )$ that are analytic in the open unit disc $U$ with $f ( 0 ) = 0$ and $f ^ { \prime } ( 0 ) = 1$ (cf. also Analytic function). Let $S$ denote the subclass of $A$ consisting of all univalent functions in $U$ (cf. also Univalent function). Further, let $S ^ { * }$ denote the subclass of $S$ consisting of functions that are starlike with respect to the origin (cf. also Univalent function).

The Kufarev differential equation

\begin{equation} \tag{a1} \frac { \partial f ( z , t ) } { \partial t } = - f ( z , t ) p ( f , t ), \end{equation}

\begin{equation} \tag{a2} \frac { \partial f ( z , t ) } { \partial t } = - z f ^ { \prime } ( z , t ) p ( z , t ), \end{equation}

where $p ( u , t ) = 1 + \alpha _ { 1 } ( t ) u + \alpha _ { 2 } ( t ) u ^ { 2 } +\dots$ is a function regular in $| u | < 1$, having positive real part and being piecewise continuous with respect to a parameter $t$, plays an important part in the theory of univalent functions. This differential equation can be generalized as the corresponding Loewner differential equation

\begin{equation} \tag{a3} \frac { \partial f ( z , t ) } { \partial t } = - f ( z , t ) \frac { 1 + k f ( z , t ) } { 1 - k f ( z , t ) }, \end{equation}

\begin{equation} \tag{a4} \frac { \partial f ( z , t ) } { \partial t } = - z f ^ { \prime } ( z , t ) \frac { 1 + k z } { 1 - k z }, \end{equation}

where $ k = k ( t )$ is a continuous complex-valued function with $| k ( t ) | = 1$ ($0 \leq t < \infty$).

Letting $\tau = e ^ { - t }$ ($0 < \tau \leq 1$), (a1) can be written in the form

\begin{equation} \tag{a5} \frac { d \tau } { \tau } = p ( f , \tau ) \frac { d f } { f }, \end{equation}

where $f = f ( z , \tau )$, $f ( z , 1 ) = z$, and $p ( f , \tau ) = 1 + \alpha _ { 1 } ( \tau ) f + \alpha _ { 2 } ( \tau ) f ^ { 2 } +\dots $ is a function regular in $| f | < 1$ with $\operatorname { Re } p ( f , \tau ) > 0$. Introducing a real parameter $a$, one sets

\begin{equation*} p _ { 1 } (\, f , \tau ) = p ( e ^ { i a \text{ln} \tau } f , \tau ). \end{equation*}

Further, making the change $\xi = e ^ { i a\operatorname{ln} \tau } f$, one obtains

\begin{equation*} \frac { d f } { f } = \frac { d \xi } { \xi } - i a \frac { d \tau } { \tau }. \end{equation*}

Making the changes $1 / p ( \xi , \tau ) = p _ { 2 } ( \xi , \tau )$ with $\operatorname { Re } p _ { 2 } ( \xi , \tau ) > 0$ and

\begin{equation*} \frac { 1 } { p _ { 2 } ( \xi , \tau ) + a i } = \frac { p _ { 3 } ( \xi , \tau ) } { 1 + a ^ { 2 } } - \frac { a i } { 1 + a ^ { 2 } } \end{equation*}

with $\operatorname { Re } p _ { 3 } ( \xi , \tau ) > 0$, one obtains

\begin{equation} \tag{a6} ( 1 + a ^ { 2 } ) \frac { d \tau } { \tau } = ( p _ { 3 } ( \xi , \tau ) - a i ) \frac { d \xi } { \xi }, \end{equation}

which is the generalization of (a5).

Writing

\begin{equation*} p _ { 3 } ( \xi , \tau ) = p _ { 0 } ( \xi ) ( 1 - \tau ^ { m } ) + p _ { 1 } ( \xi ) \tau ^ { m }\; ( m > 0 ) \end{equation*}

with

\begin{equation*} p _ { 0 } ( \xi ) = 1 + \alpha _ { 1 } \xi + \alpha _ { 2 } \xi ^ { 2 } + \ldots ( \operatorname { Re } p _ { 0 } ( \xi ) > 0 ) \end{equation*}

and

\begin{equation*} p _ { 1 } ( \xi ) = 1 + \beta _ { 1 } \xi + \beta _ { 2 } \xi ^ { 2 } + \ldots ( \operatorname { Re } p _ { 1 } ( \xi ) > 0 ), \end{equation*}

(a6) gives the Bernoulli equation

\begin{equation} \tag{a7} ( 1 + a ^ { 2 } ) \frac { d \tau } { d \xi } = \end{equation}

\begin{equation*} = ( p _ { 0 } ( \xi ) - a i ) \frac { \tau } { \xi } + ( p _ { 1 } ( \xi ) + p _ { 0 } ( \xi ) ) \frac { \tau ^ { m + 1 } } { \xi }. \end{equation*}

If one takes

\begin{equation*} \xi = e ^ { i a \operatorname { ln } \tau } f ( z , \tau ) | _ { \tau = 1 } = z \end{equation*}

in (a7), one obtains the integral

\begin{equation} \tag{a8} - \frac { 1 + a ^ { 2 } } { m } \tau ^ { - m } = \end{equation}

\begin{equation*} =e ^{-\frac { m } { 1 + a ^ { 2 } } \int _ { z } ^ { \xi } \frac { p _ { 0 } ( s ) - a i } { s } d s} \times \times \left\{ \int _ { z } ^ { \xi } \frac { p _ { 1 } ( s ) - p _ { 0 } ( s ) } { s } e^{ \frac { m } { 1 + a ^ { 2 } } \int _ { z } ^ { s } \frac { p _ { 0 } ( t ) - a i } { t } d t } d s - \frac { 1 + a ^ { 2 } } { m } \right\}. \end{equation*}

Using

\begin{equation*} \int _ { z } ^ { \xi } \frac { 1 - a i } { s } d s = \operatorname { ln } \left( \frac { \xi } { z } \right) ^ { 1 - a i } \end{equation*}

and $f e ^ { i a \operatorname { ln } \tau } = f e ^ { a i } = \xi$, one sees that $f ( z , \tau ) / \tau$ is uniformly convergent to a certain function $w = w ( z )$ of the class $S$. This implies that

\begin{equation} \tag{a9} w ^ { \frac { m } { 1 + a i } } = \end{equation}

\begin{equation*} =\frac { m } { 1 + a ^ { 2 } } \left\{ \int _ { 0 } ^ { z } \frac { p _ { 1 } ( s ) - p _ { 0 } ( s ) } { s ^ { 1 - \frac { m } { 1 + a i } } } e ^ { \frac { m } { 1 + a ^ { 2 } } \int _ { 0 } ^ { s } \frac { p _ { 0 } ( t ) - 1 } { t } d t } d s + + \frac { 1 + a ^ { 2 } } { m } z ^ { \frac { m } { 1 + a i } } e ^ { \frac { m } { 1 + a ^ { 2 } } \int _ { 0 } ^ { z } \frac { p _ { 0 } ( t ) - 1 } { t } d t} \right\}. \end{equation*}

Noting that (a9) implies

\begin{equation} \tag{a10} w ( z ) = \end{equation}

\begin{equation*} = \left\{ \frac { m } { 1 + a ^ { 2 } } \int _ { 0 } ^ { z } \frac { p _ { 1 } ( s ) - a i } { s ^ { 1 - \frac { m } { 1 + a i } } } e ^ { \frac { m } { 1 + a ^ { 2 } } \int _ { 0 } ^ { s } \frac { p _ { 0 } ( t ) - 1 } { t } d t } d s \right\}^{\frac{1+ai}{m}}, \end{equation*}

I.E. Bazilevich [a1] proved that the function $f ( z )$ given by

\begin{equation} \tag{a11} f ( z ) = \end{equation}

\begin{equation*} = \left\{ \frac { \beta } { 1 + \alpha ^ { 2 } } \int _ { 0 } ^ { z } \frac { h ( \xi ) - \alpha i } { \xi ^ { 1 + \alpha \beta i / ( 1 + \alpha ^ { 2 } ) } } g ( \xi ) ^ { \beta / ( 1 + \alpha ^ { 2 } ) } d \xi \right\} ^ { ( 1 + \alpha i ) / \beta } \end{equation*}

belongs to the class $S$, where

\begin{equation*} g ( z ) = z e ^ { \int _ { 0 } ^ { z } \frac { p _ { 0 } ( t ) - 1 } { t } d t } \in S^*, \end{equation*}

$h ( z ) = 1 + c _ { 1 } z + c _ { 2 } z ^ { 2 } + \ldots$ is regular in $U$ with $\operatorname { Re } h ( z ) > 0$, $\alpha$ is any real number, and $\beta > 0$.

If one sets $\alpha = 0$ in (a11), then

\begin{equation} \tag{a12} f ( z ) = \left( \beta \int _ { 0 } ^ { z } h ( \xi ) \xi ^ { - 1 } g ( \xi ) ^ { \beta } d \xi \right) ^ { 1 / \beta }. \end{equation}

Since $\operatorname { Re } h ( z ) > 0$ in $U$, the function $f ( z )$ given by (a12) satisfies

\begin{equation} \tag{a13} \operatorname { Re } \left\{ \frac { z f ^ { \prime } ( z ) } { f ( z ) ^ { 1 - \beta } g ( z ) ^ { \beta } } \right\} > 0 ( z \in U ). \end{equation}

Therefore, the function $f ( z )$ satisfying (a13) with $g ( z ) \in S ^ { * }$ is called a Bazilevich function of type $\beta$.

Denote by $B ( \beta )$ the class of functions $f ( z )$ that are Bazilevich of type $\beta$ in $U$.

1) If $f \in B ( \beta )$ with $| f ( z ) | < 1$ in $U$, then

\begin{equation*} L ( r ) = \int _ { 0 } ^ { 2 \pi } \left| z f ^ { \prime } ( z ) \right| d \theta = O \left( \operatorname { log } \frac { 1 } { 1 - r } \right) \end{equation*}

as $r \rightarrow 1$ (see [a3]).

2) Let 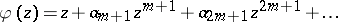be analytic in $U$. Then $\varphi ( z ) \in B ( \beta )$ if and only if $\varphi ( z ) = ( f ( z ^ { m } ) ) ^ { 1 / m }$ with $f ( z ) \in B ( \alpha / m )$ (see [a7]).

3) T. Sheil-Small [a12] has introduced the class of Bazilevich functions of type $( \alpha , \beta )$, given by

\begin{equation*} f ( z ) = \{ \int _ { 0 } ^ { z } g ^ { \alpha } ( \xi ) h ( \xi ) \xi ^ { i \beta - 1 } d \xi \} ^ { 1 / ( \alpha + i \beta ) }. \end{equation*}

4) If $f \in B ( m / n )$, then $( f ( z ^ { n } ) )^ { m / n }$ is a close-to-convex $m$-valent function, where $m / n$ is a rational number (see [a9]).

For other properties of Bazilevich functions, see [a4], [a8], [a10], [a2], [a6], [a11], and [a5].

References

[a1]	I.E. Bazilevich, "On a class of integrability by quadratures of the equation of Loewner–Kufarev" Mat. Sb. , 37 (1955) pp. 471–476
[a2]	R. Singh, "On Bazilevič functions" Proc. Amer. Math. Soc. , 38 (1973) pp. 261–271
[a3]	D.K. Thomas, "On Bazilevič functions" Trans. Amer. Math. Soc. , 132 (1968) pp. 353–361
[a4]	J. Zamorski, "On Bazilevič schlicht functions" Ann. Polon. Math. , 12 (1962) pp. 83–90
[a5]	P.L. Duren, "Univalent functions" , Grundl. Math. Wissenschaft. , 259 , Springer (1983)
[a6]	P.J. Eenigenburg, S.S. Miller, P.T. Mocanu, M.O. Reade, "On a subclass of Bazilevič functions" Proc. Amer. Math. Soc. , 45 (1974) pp. 88–92
[a7]	F.R. Keogh, S.S. Miller, "On the coefficients of Bazilevič functions" Proc. Amer. Math. Soc. , 30 (1971) pp. 492–496
[a8]	S.S. Miller, "The Hardy class of a Bazilevič function and its derivative" Proc. Amer. Math. Soc. , 30 (1971) pp. 125–132
[a9]	P.T. Mocanu, M.O. Reade, E.J. Zlotkiewicz, "On Bazilevič functions" Proc. Amer. Math. Soc. , 39 (1973) pp. 173–174
[a10]	M. Nunokawa, "On the Bazilevič analytic functions" Sci. Rep. Fac. Edu. Gunma Univ. , 21 (1972) pp. 9–13
[a11]	Ch. Pommerenke, "Univalent functions" , Vandenhoeck&Ruprecht (1975)
[a12]	T. Sheil-Small, "On Bazilevič functions" Quart. J. Math. , 23 (1972) pp. 135–142