Banach analytic space
An infinite-dimensional generalization of the concept of an analytic space, which arose in the context of the study of deformations of analytic structures (cf. Deformation). Here, the local model is a Banach analytic set, i.e. a subset  of an open set
of an open set  in a Banach space
in a Banach space  over
over  , where
, where  is an analytic mapping into the Banach space
is an analytic mapping into the Banach space  . As distinct from the finite-dimensional case, not one structure sheaf, but a set of sheaves
. As distinct from the finite-dimensional case, not one structure sheaf, but a set of sheaves 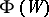 , where
, where  is an open set in an arbitrary Banach space
is an open set in an arbitrary Banach space  , is defined on the local model.
, is defined on the local model. 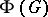 is defined as the quotient of the sheaf of germs of analytic mappings
is defined as the quotient of the sheaf of germs of analytic mappings  by the subsheaf of germs of mappings of the type
by the subsheaf of germs of mappings of the type 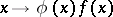 , where
, where 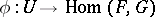 is a local analytic mapping, while
is a local analytic mapping, while  is generated by mappings which assume values in
is generated by mappings which assume values in 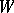 . The sheaves
. The sheaves 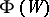 define a functor from the category
define a functor from the category 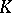 of open sets in Banach spaces and their analytic mappings into the category of sheaves of sets on
of open sets in Banach spaces and their analytic mappings into the category of sheaves of sets on 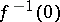 .
.
A topological space 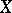 with a functor from the category
with a functor from the category 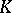 into the category of sheaves of sets in
into the category of sheaves of sets in 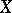 in which all points have neighbourhoods isomorphic to some local model, is said to be a Banach analytic space.
in which all points have neighbourhoods isomorphic to some local model, is said to be a Banach analytic space.
Complex-analytic spaces form a complete subcategory in the category of Banach analytic spaces. A Banach analytic space is finite-dimensional if each one of its points  has a neighbourhood that is isomorphic to a model
has a neighbourhood that is isomorphic to a model 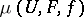 and for which there exists a mapping
and for which there exists a mapping 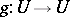 inducing an automorphism of the model and having a completely-continuous differential
inducing an automorphism of the model and having a completely-continuous differential 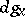 [1].
[1].
A second special case of a Banach analytic space is a Banach analytic manifold, i.e. an analytic space that is locally isomorphic to open subsets of Banach spaces. An important example is the manifold of linear subspaces of a Banach space over 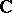 that are closed and admit closed complements.
that are closed and admit closed complements.
Finitely-defined Banach analytic sets, i.e. models of the type 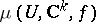 , have local properties which correspond to classical properties: primary decomposition, Hilbert's Nullstellen theorem, the local description theorem, etc., are all applicable [2].
, have local properties which correspond to classical properties: primary decomposition, Hilbert's Nullstellen theorem, the local description theorem, etc., are all applicable [2].
References
| [1] | A. Douady, "Les problèmes des modules pour les sous-espace analytique compacts d'une espace analytique donné" Ann. Inst. Fourier (Grenoble) , 16 : 1 (1966) pp. 1–95 |
| [2] | J.-P. Ramis, "Sous-ensembles analytiques d'une variété banachique complexe" , Springer (1970) |
Banach analytic space. D.A. Ponomarev (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Banach_analytic_space&oldid=11618