Algebraic homotopy

It was J.H.C. Whitehead who introduced the term "algebraic homotopy" in his address to the 1950 International Congress of Mathematicians. For him the main problems were those of describing, understanding and calculating homotopy types of spaces and homotopy classes of mappings. His work shows he attacked of this problem through several special cases.

i) Studying spaces with cells in a small range of dimensions, for example $r$-connected $n$-dimensional spaces.

ii) Stabilizing.

iii) Seeking higher-dimensional analogues of methods of combinatorial group theory. Later workers would also see algebraic homotopy as including:

iv) using general notions of homotopy in a variety of algebraic contexts. See [a11] for examples of i), ii) and iv), of algebraic models of homotopy types, and of many modes of study, for example that of rational homotopy theory. A further aspect is that "deformation" methods are essential in a variety of subjects for the purposes of classification, and the comparison of these deformations, or homotopies, in different subjects has led to new techniques and results [a2].

Important aspects of the aims of algebraic homotopy, however, are nearer to that of iii). It was early found that groups give algebraic models of pointed connected CW-complexes $X$ with zero homotopy groups above dimension one (so-called $1$-co-connected spaces; cf. also CW-complex). Whitehead found the concept of crossed module and, with S. MacLane, that these describe $2$-co-connected spaces. Since crossed modules occur in a variety of algebraic contexts, for example in the cohomology of groups, this suggested connections between homotopical ideas and wider contexts, and also that non-Abelian concepts lay behind homotopy theory. The generalization of crossed modules to crossed complexes (cf. also Crossed complex) has also been important as giving a "linear" model of a class of non-simply connected spaces, in which techniques analogous to those of the Abelian chain complexes can be applied. Whitehead also indicates the use of these crossed complexes in simple homotopy theory (cf. also Homotopy), which is an exploration of the use of elementary moves, analogous to the Tietze transformations of group presentation theory, but in all dimensions (see [a2] for a generalization of results in [a9] using crossed complexes). H.-J. Baues has also developed quadratic versions of crossed modules (see [a11], Baues' article), while crossed $n$-cubes of groups [a5], [a8] are equivalent to -groups and so also give a general model of homotopy $( n + 1 )$-types.

J.-L. Loday, starting from the problem of the obstruction to excision in algebraic $K$-theory, introduced in [a7] the notion of a 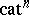-group, which is also described as an $n$-fold groupoid internal to the category of groups, and showed that they describe all homotopy $( n + 1 )$-types. While these structures are related to simplicial groups [a8], their use in homotopy theory can come under a general scheme, as follows. Here, $\Pi$ is a functor defined geometrically in terms of homotopy classes of mappings, $\mathcal{B}$ and $B$ are "classifying space functors" , and $U$ is a forgetful functor. One seeks such schemes in which $\Pi$ preserves certain useful co-limits, so that some calculations are possible; $\Pi \circ \mathcal{B}$ is naturally equivalent to $1$, giving a match of the two forms of data; and some transformation from $1$ to $\mathcal{B} \circ \Pi$ showing how much the algebraic data models the topological data:

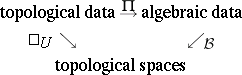There is a kind of algebraic model of all CW-spaces, namely simplicial groups and simplicial groupoids, and these form a very important tool in algebraic topology and algebraic homotopy. However it is often difficult to obtain from them specific calculations. In particular, the above scheme does not apply to simplicial groups as algebraic data, because of the lack of a functor $\Pi$ preserving certain useful co-limits. The scheme certainly applies to filtered spaces and crossed complexes, and to $n$-cubes of pointed spaces and -groups. In both cases this has led to specific calculations of homotopy types. Possibly more importantly, calculations of special cases of co-limits of these structures have led to new algebraic tools, such as a non-Abelian tensor product of groups [a3].

In any case, this scheme is related to aims of the algebraic topology of the early 20th century, to find and use in geometric situations higher-dimensional analogues of the non-Abelian fundamental group. Such an aim was long thought a mirage, but now (2000) one can see that functors to forms of multiple groupoids can play such a role. It is also interesting to see that cubical tools developed by R. Brown and P.J. Higgins in the late 1970s and related to crossed complexes are now being used in concurrency theory [a6]. This shows interesting analogies between paths in spaces and processes in computer science, and the applicability of a range of homotopical notions.

It follows from Loday's results that a surprisingly complete and simple to write down description of homotopy $n$-types is in terms of $n$-fold groupoids, described inductively as groupoids for $n = 1$ and otherwise as internal groupoids in the category of $( n - 1 )$-fold groupoids. These have a classifying space obtained by using $n$-simplicial sets. The wider implications of this need much more study.

Thus, tools developed specifically with the aim of problems in homotopy theory have been found relevant more widely. This is analogous to the way homological algebra developed from the homology and cohomology of groups to a widespread tool. In this sense, algebraic homotopy is also seen as related to or even another term for non-Abelian homological algebra, yielding rather general algebraic structures available as coefficients, or for analyzing a wide range of geometric, combinatorial or algebraic situations. As an example of this, see [a4].

In [a10] it is shown how the non-Abelian methods of algebraic homotopy have some impact on generalized Galois theories, for example in relation to central extensions of groups.

References

[a1]	R. Brown, "Higher dimensional group theory" web article (1998) (www.bangor.ac.uk/~mas010/hdaweb2.html) MR0662433 Zbl 0484.55007
[a2]	H.-J. Baues, "Algebraic homotopy" , Cambridge Univ. Press (1989) MR0985099 Zbl 0688.55001
[a3]	R. Brown, J.-L. Loday, "Van Kampen theorems for diagrams of spaces" Topology , 26 (1987) pp. 311–334 MR0899052 Zbl 0622.55009
[a4]	L. Breen, , Braided $n$-Catgories and $\sigma$-Structures in Higher Category Theory (Evanston, Ill. 1997) , Amer. Math. Soc. (1998) pp. 59–81
[a5]	G.J. Ellis, R. Steiner, "Higher-dimensional crossed modules and the homotopy groups of $( n + 1 )$-ads" J. Pure Appl. Algebra , 46 (1987) pp. 117–136 MR897011
[a6]	P. Gaucher, "Homotopy theory of higher dimensional categories and concurrency in computer science" Math. Struct. Computer Sci. , 10 (2000) pp. 481–524
[a7]	J.-L. Loday, "Spaces with finitely many homotopy groups" J. Pure Appl. Algebra , 24 (1982) pp. 179–202 MR651845 Zbl 0491.55004
[a8]	T. Porter, "$n$-types of simplicial groups and crossed $n$-cubes" Topology , 32 (1993) pp. 5–24
[a9]	J.H.C. Whitehead, "Simple homotopy type" Amer. J. Math. , 72 (1950) pp. 1–57 MR0035437
[a10]	F. Borceux, G. Janelidze, "Galois theories" , Cambridge Univ. Press (2001) MR1822890 Zbl 0978.12004
[a11]	"Handbook of algebraic topology" I.M. James (ed.) , Elsevier (1995) MR1361885 Zbl 0824.00017