*-Autonomous category
Let $\mathcal{C}$ be a symmetric closed monoidal category (cf. also Category). A functor $( - ) ^ { * } : \cal C ^ { \operatorname{op} } \rightarrow C$ is a duality functor if there exists an isomorphism $d ( A , B ) : B ^ { A } \overset{\cong}{\rightarrow} A ^ { * } B ^ { * }$, natural in $A$ and $B$, such that for all objects $A , B , C \in \mathcal{C}$ the following diagram commutes:
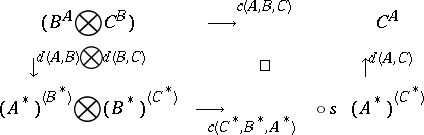 |
where in the bottom arrow $s = s ( ( A ^ { * } ) ^ { ( B ^ { * } ) } , ( B ^ { * } ) ^ { ( C ^ { * } ) } )$.
A category is $*$-autonomous if it is a symmetric monoidal closed category with a given duality functor.
It so happens that $*$-autonomous categories have real-life applications: they are models of (at least the finite part of) linear logic [a2] and have uses in modelling processes.
An example of a $*$-autonomous category is the category $\mathcal{R} \text{el}$ of sets and relations; duality is given by $S ^ { * } = S$. In fact, $B ^ { A } \cong ( A ^ { * } \otimes B )$.
From a given symmetric monoidal closed category and an object in it (that serves as a dualizing object) one can construct a $*$-autonomous category (the so-called Chu construction, [a3]). It can be viewed as a kind of generalized topology.
References
| [a1] | M. Barr, "$*$-Autonomous categories" , Lecture Notes in Mathematics , 752 , Springer (1979) |
| [a2] | M. Barr, C. Wells, "Category theory for computing science" , Publ. CRM (1990) |
| [a3] | P.-H. Chu, "Constructing $*$-autonomous categories" M. Barr (ed.) , $*$-Autonomous categories , Lecture Notes in Mathematics , 752 , Springer (1979) pp. Appendix |
*-Autonomous category. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=*-Autonomous_category&oldid=50786