|
|
| Line 1: |
Line 1: |
| − | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x1200102.png" />-inner automorphisms were introduced by V.K. Kharchenko in [[#References|[a2]]] and [[#References|[a3]]] to study both prime rings satisfying generalized identities and the Galois theory of semi-prime rings (cf. also [[Prime ring|Prime ring]]; [[Rings and algebras|Rings and algebras]]). Since the appropriate definitions are much simpler when the ring is assumed to be prime, this special case is treated first here. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x1200103.png" /> be a [[Prime ring|prime ring]] (with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x1200104.png" />) and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x1200105.png" /> denote its symmetric [[Martindale ring of quotients|Martindale ring of quotients]]. Then any [[Automorphism|automorphism]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x1200106.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x1200107.png" /> extends uniquely to an automorphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x1200108.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x1200109.png" />, and one says that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001010.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001012.png" />-inner if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001013.png" /> is inner on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001014.png" /> (cf. also [[Inner automorphism|Inner automorphism]]). It is easy to see that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001015.png" />, the set of all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001016.png" />-inner automorphisms of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001017.png" />, is a [[Normal subgroup|normal subgroup]] of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001018.png" />. | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, |
| | + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist |
| | + | was used. |
| | + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. |
| | | | |
| − | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001019.png" />-inner automorphisms control the generalized linear identities of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001020.png" />, namely those linear identities which involve automorphisms. For example, it is shown in [[#References|[a2]]] that if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001021.png" /> and if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001022.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001023.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001024.png" />, then there exists a unit <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001025.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001026.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001027.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001028.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001029.png" />. In particular, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001030.png" /> is the inner automorphism of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001031.png" /> induced by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001032.png" /> and consequently <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001033.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001034.png" />-inner. Of course, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001035.png" /> is determined by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001036.png" /> up to multiplication by a non-zero element of the extended centroid <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001037.png" />.
| + | Out of 116 formulas, 114 were replaced by TEX code.--> |
| | | | |
| − | Now, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001038.png" /> be a group of automorphisms of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001039.png" /> and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001040.png" />, so that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001041.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001042.png" /> denotes the linear span of all units <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001043.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001044.png" /> such that conjugation by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001045.png" /> belongs to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001046.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001047.png" /> is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001048.png" />-subalgebra of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001049.png" />, called the algebra of the group (cf. also [[Group algebra|Group algebra]]). One says that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001050.png" /> is an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001052.png" />-group (Maschke group) if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001053.png" /> and if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001054.png" /> is a finite-dimensional semi-simple <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001055.png" />-algebra. Furthermore, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001056.png" /> is an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001058.png" />-group (Noether group) if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001059.png" /> is an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001060.png" />-group and if conjugation by every unit of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001061.png" /> induces an automorphism of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001062.png" /> contained in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001063.png" />. The Galois theory, as developed in [[#References|[a3]]] and [[#References|[a14]]], involves the action of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001064.png" />-groups and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001065.png" />-groups on prime rings.
| + | {{TEX|semi-auto}}{{TEX|partial}} |
| | + | $X$-inner automorphisms were introduced by V.K. Kharchenko in [[#References|[a2]]] and [[#References|[a3]]] to study both prime rings satisfying generalized identities and the Galois theory of semi-prime rings (cf. also [[Prime ring|Prime ring]]; [[Rings and algebras|Rings and algebras]]). Since the appropriate definitions are much simpler when the ring is assumed to be prime, this special case is treated first here. Let $R$ be a [[Prime ring|prime ring]] (with $1$) and let $Q = Q _ { s } ( R )$ denote its symmetric [[Martindale ring of quotients|Martindale ring of quotients]]. Then any [[Automorphism|automorphism]] $\sigma$ of $R$ extends uniquely to an automorphism $\hat { \sigma }$ of $Q$, and one says that $\sigma$ is $X$-inner if $\hat { \sigma }$ is inner on $Q$ (cf. also [[Inner automorphism|Inner automorphism]]). It is easy to see that $\operatorname{Inn} ( R )$, the set of all $X$-inner automorphisms of $R$, is a [[Normal subgroup|normal subgroup]] of $\operatorname{Aut}( R )$. |
| | | | |
| − | Note that if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001066.png" /> is an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001067.png" />-group and if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001068.png" /> is a unit of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001069.png" />, then conjugation by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001070.png" /> need not stabilize <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001071.png" />. Thus, it is not always possible to embed an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001072.png" />-group into an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001073.png" />-group. One can avoid this difficulty by extending the definition of "automorphism of R" to include those (real) automorphisms <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001074.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001075.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001076.png" /> for some <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001077.png" />.
| + | $X$-inner automorphisms control the generalized linear identities of $R$, namely those linear identities which involve automorphisms. For example, it is shown in [[#References|[a2]]] that if $0 \neq a , b , c , d \in R$ and if $\sigma \in \operatorname { Aut } ( R )$ with $a x b = c x ^ { \sigma } d$ for all $x \in R$, then there exists a unit $q \in Q$ with $c = a q$, $d = q ^ { - 1 } b$ and $x ^ { \sigma } = q ^ { - 1 } x q$ for all $x \in R$. In particular, $\hat { \sigma }$ is the inner automorphism of $Q$ induced by $q$ and consequently $\sigma$ is $X$-inner. Of course, $q$ is determined by $\sigma$ up to multiplication by a non-zero element of the extended centroid $C = \mathbf{Z} ( Q ) = \mathbf{C} _ { Q } ( R )$. |
| | | | |
| − | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001078.png" />-inner automorphisms also appear prominently in the study of cross products. For example, it is proved in [[#References|[a1]]] that if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001079.png" /> is a [[Cross product|cross product]] over the prime ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001080.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001081.png" /> embeds naturally into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001082.png" /> and that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001083.png" /> is a twisted group algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001084.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001085.png" />. Furthermore, it is shown in [[#References|[a9]]] that every non-zero ideal of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001086.png" /> meets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001087.png" /> non-trivially, and in [[#References|[a11]]] that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001088.png" /> is prime (or semi-prime) if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001089.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001090.png" />-prime (or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001091.png" />-semi-prime) for all finite normal subgroups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001092.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001093.png" /> contained in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001094.png" />. The above-mentioned structure of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001095.png" /> is also used in [[#References|[a5]]] and [[#References|[a6]]] to precisely describe the prime ideals in cross products of finite and of polycyclic-by-finite groups.
| + | Now, let $G$ be a group of automorphisms of $R$ and let $G _ { \text { inn } } = G \cap \operatorname { lnn } ( R )$, so that $G _ { \operatorname{inn} } \triangleleft G$. If $B ( G )$ denotes the linear span of all units $q$ in $Q$ such that conjugation by $q$ belongs to $\hat { G }_{\text{inn}}$, then $B ( G )$ is a $C$-subalgebra of $Q$, called the algebra of the group (cf. also [[Group algebra|Group algebra]]). One says that $G$ is an $M$-group (Maschke group) if $|G:G_{\text{inn}}|< \infty$ and if $B ( G )$ is a finite-dimensional semi-simple $C$-algebra. Furthermore, $G$ is an $N$-group (Noether group) if $G$ is an $M$-group and if conjugation by every unit of $B ( G )$ induces an automorphism of $R$ contained in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001063.png"/>. The Galois theory, as developed in [[#References|[a3]]] and [[#References|[a14]]], involves the action of $M$-groups and $N$-groups on prime rings. |
| | | | |
| − | There are numerous computations of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001096.png" /> in the literature. To start with, it is shown in [[#References|[a4]]] that if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001097.png" /> is a non-commutative free algebra, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001098.png" />. More general free products are studied in [[#References|[a7]]] and [[#References|[a8]]]. Next, [[#References|[a10]]] effectively handles graded domains like enveloping algebras of Lie algebras, and [[#References|[a15]]] considers arbitrary enveloping algebra smash products. Finally, [[#References|[a12]]] and [[#References|[a13]]] study certain group algebras and show that for any group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001099.png" /> there exists a domain <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x120010100.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x120010101.png" />.
| + | Note that if $G$ is an $M$-group and if $q$ is a unit of $B ( G )$, then conjugation by $q$ need not stabilize $R$. Thus, it is not always possible to embed an $M$-group into an $N$-group. One can avoid this difficulty by extending the definition of "automorphism of R" to include those (real) automorphisms $\tau$ of $Q$ such that $\tau ( A ) \subseteq R$ for some $0 \neq A \lhd R$. |
| | | | |
| − | Now suppose that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x120010102.png" /> is a semi-prime ring and again let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x120010103.png" /> denote its symmetric Martindale ring of quotients. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x120010104.png" /> is an arbitrary automorphism of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x120010105.png" />, write <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x120010106.png" />. Then, following [[#References|[a2]]], one says that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x120010107.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x120010109.png" />-inner if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x120010110.png" />. Of course, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x120010111.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x120010113.png" />-outer when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x120010114.png" />. Note that, in the case of semi-prime rings, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x120010115.png" /> need not be a subgroup of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x120010116.png" />. Nevertheless, a good deal of structure still exists. For example, [[#References|[a3]]] proves the key fact that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x120010117.png" /> is always a cyclic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x120010118.png" />-module.
| + | $X$-inner automorphisms also appear prominently in the study of cross products. For example, it is proved in [[#References|[a1]]] that if $R * G$ is a [[Cross product|cross product]] over the prime ring $R$, then $R * G$ embeds naturally into $S = Q ^ { * } G$ and that $\mathbf{C} _ { S } ( R ) = \mathbf{C} _ { S } ( Q )$ is a twisted group algebra $C ^ { t } [ G _ { \text { inn } } ]$ with $Q ^ { * } G _ { \text { inn } } = Q \otimes _ { C } C ^ { t } [ G _ { \text { inn } } ]$. Furthermore, it is shown in [[#References|[a9]]] that every non-zero ideal of $R * G$ meets $R ^ { * } G _ { \text { inn } }$ non-trivially, and in [[#References|[a11]]] that $R * G$ is prime (or semi-prime) if and only if $R ^ { * } N$ is $G$-prime (or $G$-semi-prime) for all finite normal subgroups $N$ of $G$ contained in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x12001094.png"/>. The above-mentioned structure of $R * G$ is also used in [[#References|[a5]]] and [[#References|[a6]]] to precisely describe the prime ideals in cross products of finite and of polycyclic-by-finite groups. |
| | + | |
| | + | There are numerous computations of $\operatorname{Inn} ( R )$ in the literature. To start with, it is shown in [[#References|[a4]]] that if $F$ is a non-commutative free algebra, then $\operatorname { lnn } ( F ) = \langle 1 \rangle$. More general free products are studied in [[#References|[a7]]] and [[#References|[a8]]]. Next, [[#References|[a10]]] effectively handles graded domains like enveloping algebras of Lie algebras, and [[#References|[a15]]] considers arbitrary enveloping algebra smash products. Finally, [[#References|[a12]]] and [[#References|[a13]]] study certain group algebras and show that for any group $H$ there exists a domain $R$ with $\operatorname { Aut } ( R ) / \operatorname { lnn } ( R ) \cong H$. |
| | + | |
| | + | Now suppose that $R$ is a semi-prime ring and again let $Q = Q _ { s } ( R )$ denote its symmetric Martindale ring of quotients. If $\sigma$ is an arbitrary automorphism of $R$, write $\Phi _ { \sigma } = \{ q \in Q : q x ^ { \sigma } = x q \text { for all } x \in R \}$. Then, following [[#References|[a2]]], one says that $\sigma$ is $X$-inner if $\Phi _ { \sigma } \neq 0$. Of course, $\sigma$ is $X$-outer when $\Phi _ { \sigma } = 0$. Note that, in the case of semi-prime rings, $\operatorname{Inn} ( R )$ need not be a subgroup of $\operatorname{Aut}( R )$. Nevertheless, a good deal of structure still exists. For example, [[#References|[a3]]] proves the key fact that $\Phi _ { \sigma }$ is always a cyclic $C$-module. |
| | | | |
| | ====References==== | | ====References==== |
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J.W. Fisher, S. Montgomery, "Semiprime skew group rings" ''J. Algebra'' , '''52''' (1978) pp. 241–247</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> V.K. Kharchenko, "Generalized identities with automorphisms" ''Algebra and Logic'' , '''14''' (1976) pp. 132–148 ''Algebra i Logika'' , '''14''' (1975) pp. 215–237</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> V.K. Kharchenko, "Galois theory of semiprime rings" ''Algebra and Logic'' , '''16''' (1978) pp. 208–258 ''Algebra i Logika'' , '''16''' (1977) pp. 313–363</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> V.K. Kharchenko, "Algebras of invariants of free algebras" ''Algebra and Logic'' , '''17''' (1979) pp. 316–321 ''Algebra i Logika'' , '''17''' (1978) pp. 478–487</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> M. Lorenz, D.S. Passman, "Prime ideals in crossed products of finite groups" ''Israel J. Math.'' , '''33''' (1979) pp. 89–132</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> M. Lorenz, D.S. Passman, "Prime ideals in group algebras of polycyclic-by-finite groups" ''Proc. London Math. Soc.'' , '''43''' (1981) pp. 520–543</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> W.S. Martindale III, "The normal closure of the coproduct of rings over a division ring" ''Trans. Amer. Math. Soc.'' , '''293''' (1986) pp. 303–317</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> W.S. Martindale III, S. Montgomery, "The normal closure of coproducts of domains" ''J. Algebra'' , '''82''' (1983) pp. 1–17</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> S. Montgomery, "Outer automorphisms of semi-prime rings" ''J. London Math. Soc.'' , '''18''' : 2 (1978) pp. 209–220</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> S. Montgomery, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x120010119.png" />-inner automorphisms of filtered algebras" ''Proc. Amer. Math. Soc.'' , '''83''' (1981) pp. 263–268</TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> S. Montgomery, D.S. Passman, "Crossed products over prime rings" ''Israel J. Math.'' , '''31''' (1978) pp. 224–256</TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> S. Montgomery, D.S. Passman, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x120010120.png" />-Inner automorphisms of group rings" ''Houston J. Math.'' , '''7''' (1981) pp. 395–402</TD></TR><TR><TD valign="top">[a13]</TD> <TD valign="top"> S. Montgomery, D.S. Passman, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x120010121.png" />-Inner automorphisms of group rings II" ''Houston J. Math.'' , '''8''' (1982) pp. 537–544</TD></TR><TR><TD valign="top">[a14]</TD> <TD valign="top"> S. Montgomery, D.S. Passman, "Galois theory of prime rings" ''J. Pure Appl. Algebra'' , '''31''' (1984) pp. 139–184</TD></TR><TR><TD valign="top">[a15]</TD> <TD valign="top"> J. Osterburg, D.S. Passman, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/x/x120/x120010/x120010122.png" />-inner automorphisms of enveloping rings" ''J. Algebra'' , '''130''' (1990) pp. 412–434</TD></TR></table> | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> J.W. Fisher, S. Montgomery, "Semiprime skew group rings" ''J. Algebra'' , '''52''' (1978) pp. 241–247</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> V.K. Kharchenko, "Generalized identities with automorphisms" ''Algebra and Logic'' , '''14''' (1976) pp. 132–148 ''Algebra i Logika'' , '''14''' (1975) pp. 215–237</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> V.K. Kharchenko, "Galois theory of semiprime rings" ''Algebra and Logic'' , '''16''' (1978) pp. 208–258 ''Algebra i Logika'' , '''16''' (1977) pp. 313–363</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> V.K. Kharchenko, "Algebras of invariants of free algebras" ''Algebra and Logic'' , '''17''' (1979) pp. 316–321 ''Algebra i Logika'' , '''17''' (1978) pp. 478–487</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> M. Lorenz, D.S. Passman, "Prime ideals in crossed products of finite groups" ''Israel J. Math.'' , '''33''' (1979) pp. 89–132</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> M. Lorenz, D.S. Passman, "Prime ideals in group algebras of polycyclic-by-finite groups" ''Proc. London Math. Soc.'' , '''43''' (1981) pp. 520–543</td></tr><tr><td valign="top">[a7]</td> <td valign="top"> W.S. Martindale III, "The normal closure of the coproduct of rings over a division ring" ''Trans. Amer. Math. Soc.'' , '''293''' (1986) pp. 303–317</td></tr><tr><td valign="top">[a8]</td> <td valign="top"> W.S. Martindale III, S. Montgomery, "The normal closure of coproducts of domains" ''J. Algebra'' , '''82''' (1983) pp. 1–17</td></tr><tr><td valign="top">[a9]</td> <td valign="top"> S. Montgomery, "Outer automorphisms of semi-prime rings" ''J. London Math. Soc.'' , '''18''' : 2 (1978) pp. 209–220</td></tr><tr><td valign="top">[a10]</td> <td valign="top"> S. Montgomery, "$X$-inner automorphisms of filtered algebras" ''Proc. Amer. Math. Soc.'' , '''83''' (1981) pp. 263–268</td></tr><tr><td valign="top">[a11]</td> <td valign="top"> S. Montgomery, D.S. Passman, "Crossed products over prime rings" ''Israel J. Math.'' , '''31''' (1978) pp. 224–256</td></tr><tr><td valign="top">[a12]</td> <td valign="top"> S. Montgomery, D.S. Passman, "$X$-Inner automorphisms of group rings" ''Houston J. Math.'' , '''7''' (1981) pp. 395–402</td></tr><tr><td valign="top">[a13]</td> <td valign="top"> S. Montgomery, D.S. Passman, "$X$-Inner automorphisms of group rings II" ''Houston J. Math.'' , '''8''' (1982) pp. 537–544</td></tr><tr><td valign="top">[a14]</td> <td valign="top"> S. Montgomery, D.S. Passman, "Galois theory of prime rings" ''J. Pure Appl. Algebra'' , '''31''' (1984) pp. 139–184</td></tr><tr><td valign="top">[a15]</td> <td valign="top"> J. Osterburg, D.S. Passman, "$X$-inner automorphisms of enveloping rings" ''J. Algebra'' , '''130''' (1990) pp. 412–434</td></tr></table> |
$X$-inner automorphisms were introduced by V.K. Kharchenko in [a2] and [a3] to study both prime rings satisfying generalized identities and the Galois theory of semi-prime rings (cf. also Prime ring; Rings and algebras). Since the appropriate definitions are much simpler when the ring is assumed to be prime, this special case is treated first here. Let $R$ be a prime ring (with $1$) and let $Q = Q _ { s } ( R )$ denote its symmetric Martindale ring of quotients. Then any automorphism $\sigma$ of $R$ extends uniquely to an automorphism $\hat { \sigma }$ of $Q$, and one says that $\sigma$ is $X$-inner if $\hat { \sigma }$ is inner on $Q$ (cf. also Inner automorphism). It is easy to see that $\operatorname{Inn} ( R )$, the set of all $X$-inner automorphisms of $R$, is a normal subgroup of $\operatorname{Aut}( R )$.
$X$-inner automorphisms control the generalized linear identities of $R$, namely those linear identities which involve automorphisms. For example, it is shown in [a2] that if $0 \neq a , b , c , d \in R$ and if $\sigma \in \operatorname { Aut } ( R )$ with $a x b = c x ^ { \sigma } d$ for all $x \in R$, then there exists a unit $q \in Q$ with $c = a q$, $d = q ^ { - 1 } b$ and $x ^ { \sigma } = q ^ { - 1 } x q$ for all $x \in R$. In particular, $\hat { \sigma }$ is the inner automorphism of $Q$ induced by $q$ and consequently $\sigma$ is $X$-inner. Of course, $q$ is determined by $\sigma$ up to multiplication by a non-zero element of the extended centroid $C = \mathbf{Z} ( Q ) = \mathbf{C} _ { Q } ( R )$.
Now, let $G$ be a group of automorphisms of $R$ and let $G _ { \text { inn } } = G \cap \operatorname { lnn } ( R )$, so that $G _ { \operatorname{inn} } \triangleleft G$. If $B ( G )$ denotes the linear span of all units $q$ in $Q$ such that conjugation by $q$ belongs to $\hat { G }_{\text{inn}}$, then $B ( G )$ is a $C$-subalgebra of $Q$, called the algebra of the group (cf. also Group algebra). One says that $G$ is an $M$-group (Maschke group) if $|G:G_{\text{inn}}|< \infty$ and if $B ( G )$ is a finite-dimensional semi-simple $C$-algebra. Furthermore, $G$ is an $N$-group (Noether group) if $G$ is an $M$-group and if conjugation by every unit of $B ( G )$ induces an automorphism of $R$ contained in 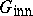 . The Galois theory, as developed in [a3] and [a14], involves the action of $M$-groups and $N$-groups on prime rings.
. The Galois theory, as developed in [a3] and [a14], involves the action of $M$-groups and $N$-groups on prime rings.
Note that if $G$ is an $M$-group and if $q$ is a unit of $B ( G )$, then conjugation by $q$ need not stabilize $R$. Thus, it is not always possible to embed an $M$-group into an $N$-group. One can avoid this difficulty by extending the definition of "automorphism of R" to include those (real) automorphisms $\tau$ of $Q$ such that $\tau ( A ) \subseteq R$ for some $0 \neq A \lhd R$.
$X$-inner automorphisms also appear prominently in the study of cross products. For example, it is proved in [a1] that if $R * G$ is a cross product over the prime ring $R$, then $R * G$ embeds naturally into $S = Q ^ { * } G$ and that $\mathbf{C} _ { S } ( R ) = \mathbf{C} _ { S } ( Q )$ is a twisted group algebra $C ^ { t } [ G _ { \text { inn } } ]$ with $Q ^ { * } G _ { \text { inn } } = Q \otimes _ { C } C ^ { t } [ G _ { \text { inn } } ]$. Furthermore, it is shown in [a9] that every non-zero ideal of $R * G$ meets $R ^ { * } G _ { \text { inn } }$ non-trivially, and in [a11] that $R * G$ is prime (or semi-prime) if and only if $R ^ { * } N$ is $G$-prime (or $G$-semi-prime) for all finite normal subgroups $N$ of $G$ contained in 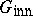 . The above-mentioned structure of $R * G$ is also used in [a5] and [a6] to precisely describe the prime ideals in cross products of finite and of polycyclic-by-finite groups.
. The above-mentioned structure of $R * G$ is also used in [a5] and [a6] to precisely describe the prime ideals in cross products of finite and of polycyclic-by-finite groups.
There are numerous computations of $\operatorname{Inn} ( R )$ in the literature. To start with, it is shown in [a4] that if $F$ is a non-commutative free algebra, then $\operatorname { lnn } ( F ) = \langle 1 \rangle$. More general free products are studied in [a7] and [a8]. Next, [a10] effectively handles graded domains like enveloping algebras of Lie algebras, and [a15] considers arbitrary enveloping algebra smash products. Finally, [a12] and [a13] study certain group algebras and show that for any group $H$ there exists a domain $R$ with $\operatorname { Aut } ( R ) / \operatorname { lnn } ( R ) \cong H$.
Now suppose that $R$ is a semi-prime ring and again let $Q = Q _ { s } ( R )$ denote its symmetric Martindale ring of quotients. If $\sigma$ is an arbitrary automorphism of $R$, write $\Phi _ { \sigma } = \{ q \in Q : q x ^ { \sigma } = x q \text { for all } x \in R \}$. Then, following [a2], one says that $\sigma$ is $X$-inner if $\Phi _ { \sigma } \neq 0$. Of course, $\sigma$ is $X$-outer when $\Phi _ { \sigma } = 0$. Note that, in the case of semi-prime rings, $\operatorname{Inn} ( R )$ need not be a subgroup of $\operatorname{Aut}( R )$. Nevertheless, a good deal of structure still exists. For example, [a3] proves the key fact that $\Phi _ { \sigma }$ is always a cyclic $C$-module.
References
| [a1] | J.W. Fisher, S. Montgomery, "Semiprime skew group rings" J. Algebra , 52 (1978) pp. 241–247 |
| [a2] | V.K. Kharchenko, "Generalized identities with automorphisms" Algebra and Logic , 14 (1976) pp. 132–148 Algebra i Logika , 14 (1975) pp. 215–237 |
| [a3] | V.K. Kharchenko, "Galois theory of semiprime rings" Algebra and Logic , 16 (1978) pp. 208–258 Algebra i Logika , 16 (1977) pp. 313–363 |
| [a4] | V.K. Kharchenko, "Algebras of invariants of free algebras" Algebra and Logic , 17 (1979) pp. 316–321 Algebra i Logika , 17 (1978) pp. 478–487 |
| [a5] | M. Lorenz, D.S. Passman, "Prime ideals in crossed products of finite groups" Israel J. Math. , 33 (1979) pp. 89–132 |
| [a6] | M. Lorenz, D.S. Passman, "Prime ideals in group algebras of polycyclic-by-finite groups" Proc. London Math. Soc. , 43 (1981) pp. 520–543 |
| [a7] | W.S. Martindale III, "The normal closure of the coproduct of rings over a division ring" Trans. Amer. Math. Soc. , 293 (1986) pp. 303–317 |
| [a8] | W.S. Martindale III, S. Montgomery, "The normal closure of coproducts of domains" J. Algebra , 82 (1983) pp. 1–17 |
| [a9] | S. Montgomery, "Outer automorphisms of semi-prime rings" J. London Math. Soc. , 18 : 2 (1978) pp. 209–220 |
| [a10] | S. Montgomery, "$X$-inner automorphisms of filtered algebras" Proc. Amer. Math. Soc. , 83 (1981) pp. 263–268 |
| [a11] | S. Montgomery, D.S. Passman, "Crossed products over prime rings" Israel J. Math. , 31 (1978) pp. 224–256 |
| [a12] | S. Montgomery, D.S. Passman, "$X$-Inner automorphisms of group rings" Houston J. Math. , 7 (1981) pp. 395–402 |
| [a13] | S. Montgomery, D.S. Passman, "$X$-Inner automorphisms of group rings II" Houston J. Math. , 8 (1982) pp. 537–544 |
| [a14] | S. Montgomery, D.S. Passman, "Galois theory of prime rings" J. Pure Appl. Algebra , 31 (1984) pp. 139–184 |
| [a15] | J. Osterburg, D.S. Passman, "$X$-inner automorphisms of enveloping rings" J. Algebra , 130 (1990) pp. 412–434 |
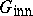 . The Galois theory, as developed in [a3] and [a14], involves the action of $M$-groups and $N$-groups on prime rings.
. The Galois theory, as developed in [a3] and [a14], involves the action of $M$-groups and $N$-groups on prime rings.
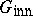 . The above-mentioned structure of $R * G$ is also used in [a5] and [a6] to precisely describe the prime ideals in cross products of finite and of polycyclic-by-finite groups.
. The above-mentioned structure of $R * G$ is also used in [a5] and [a6] to precisely describe the prime ideals in cross products of finite and of polycyclic-by-finite groups.