Weyl group
The Weyl group of symmetries of a root system. Depending on the actual realization of the root system, different Weyl groups are considered: Weyl groups of a semi-simple splittable Lie algebra, of a symmetric space, of an algebraic group, etc.
Let 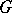 be a connected affine algebraic group defined over an algebraically closed field
be a connected affine algebraic group defined over an algebraically closed field 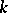 . The Weyl group of
. The Weyl group of 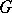 with respect to a torus
with respect to a torus 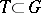 is the quotient group
is the quotient group
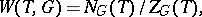 |
considered as a group of automorphisms of  induced by the conjugations of
induced by the conjugations of  by elements of
by elements of  . Here
. Here 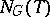 is the normalizer (cf. Normalizer of a subset) and
is the normalizer (cf. Normalizer of a subset) and 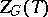 is the centralizer of
is the centralizer of 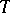 in
in 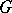 . The group
. The group 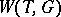 is finite. If
is finite. If 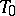 is a maximal torus,
is a maximal torus, 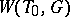 is said to be the Weyl group
is said to be the Weyl group 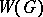 of the algebraic group
of the algebraic group 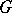 . This definition does not depend on the choice of a maximal torus
. This definition does not depend on the choice of a maximal torus 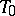 (up to isomorphism). The action by conjugation of
(up to isomorphism). The action by conjugation of  on the set
on the set 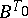 of Borel subgroups (cf. Borel subgroup) in
of Borel subgroups (cf. Borel subgroup) in 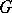 containing
containing 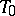 induces a simply transitive action of
induces a simply transitive action of 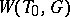 on
on 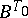 . The action by conjugation of
. The action by conjugation of 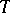 on
on 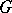 induces an adjoint action of
induces an adjoint action of 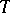 on the Lie algebra
on the Lie algebra 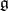 of
of 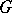 . Let
. Let 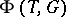 be the set of non-zero weights of the weight decomposition of
be the set of non-zero weights of the weight decomposition of 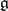 with respect to this action, which means that
with respect to this action, which means that 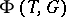 is the root system of
is the root system of 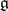 with respect to
with respect to 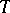 (cf. Weight of a representation of a Lie algebra).
(cf. Weight of a representation of a Lie algebra). 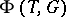 is a subset of the group
is a subset of the group 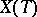 of rational characters of the torus
of rational characters of the torus 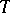 , and
, and 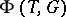 is invariant with respect to the action of
is invariant with respect to the action of 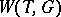 on
on 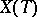 .
.
Let 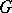 be a reductive group, let
be a reductive group, let 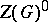 be the connected component of the identity of its centre and let
be the connected component of the identity of its centre and let 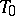 be a maximal torus of
be a maximal torus of 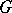 . The vector space
. The vector space
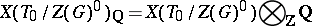 |
is canonically identified with a subspace of the vector space
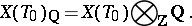 |
As a subset of 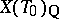 , the set
, the set 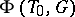 is a reduced root system in
is a reduced root system in 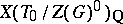 , and the natural action of
, and the natural action of 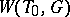 on
on 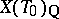 defines an isomorphism between
defines an isomorphism between 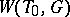 and the Weyl group of the root system
and the Weyl group of the root system 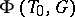 . Thus,
. Thus, 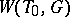 displays all the properties of a Weyl group of a reduced root system; e.g. it is generated by reflections (cf. Reflection).
displays all the properties of a Weyl group of a reduced root system; e.g. it is generated by reflections (cf. Reflection).
The Weyl group of a Tits system is a generalization of this situation (for its exact definition see Tits system).
The Weyl group 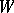 of a finite-dimensional reductive Lie algebra
of a finite-dimensional reductive Lie algebra 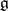 over an algebraically closed field of characteristic zero is defined as the Weyl group of its adjoint group. The adjoint action of
over an algebraically closed field of characteristic zero is defined as the Weyl group of its adjoint group. The adjoint action of 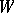 in the Cartan subalgebra
in the Cartan subalgebra 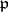 of
of 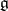 is a faithful representation of
is a faithful representation of 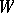 . The group
. The group 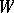 is often identified with the image of this representation, being regarded as the corresponding linear group in
is often identified with the image of this representation, being regarded as the corresponding linear group in 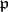 generated by the reflections. The concept of a "Weyl group" was first used by H. Weyl
generated by the reflections. The concept of a "Weyl group" was first used by H. Weyl
in the special case of finite-dimensional semi-simple Lie algebras over the field of complex numbers. A Weyl group may also be defined for an arbitrary splittable semi-simple finite-dimensional Lie algebra, as the Weyl group of its root system. A relative Weyl group may be defined for an affine algebraic group 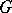 defined over an algebraically non-closed field. If
defined over an algebraically non-closed field. If 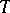 is a maximal
is a maximal 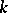 -split torus of
-split torus of 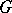 , then the quotient group
, then the quotient group 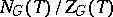 (the normalizer of
(the normalizer of 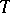 over its centralizer in
over its centralizer in 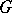 ), regarded as the group of automorphisms of
), regarded as the group of automorphisms of 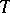 induced by the conjugations of
induced by the conjugations of 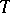 by elements of
by elements of 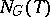 , is said to be the relative Weyl group of
, is said to be the relative Weyl group of 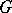 .
.
For the Weyl group of a symmetric space, see Symmetric space. The Weyl group of a real connected non-compact semi-simple algebraic group is identical with the Weyl group of the corresponding symmetric space. For the affine Weyl group see Root system.
References
| [1a] | H. Weyl, "Theorie der Darstellung kontinuierlicher halb-einfacher Gruppen durch linearen Transformationen I" Math. Z. , 23 (1925) pp. 271–309 |
| [1b] | H. Weyl, "Theorie der Darstellung kontinuierlicher halb-einfacher Gruppen durch linearen Transformationen II" Math. Z. , 24 (1925) pp. 328–395 |
| [2] | A. Borel, "Linear algebraic groups" , Benjamin (1969) |
| [3] | N. Jacobson, "Lie algebras" , Interscience (1962) ((also: Dover, reprint, 1979)) |
| [4] | N. Bourbaki, "Lie groups and Lie algebras" , Elements of mathematics , Hermann (1975) (Translated from French) |
| [5a] | A. Borel, J. Tits, "Groupes réductifs" Publ. Math. I.H.E.S. , 27 (1965) pp. 55–150 |
| [5b] | A. Borel, J. Tits, "Complément à l'article "Groupes réductifs" " Publ. Math. I.H.E.S. , 41 (1972) pp. 253–276 |
| [6] | F. Bruhat, J. Tits, "Groupes algébriques simples sur un corps local" T.A. Springer (ed.) et al. (ed.) , Proc. Conf. local fields (Driebergen, 1966) , Springer (1967) pp. 23–36 |
| [7] | S. Helgason, "Differential geometry and symmetric spaces" , Acad. Press (1962) |
Comments
The affine Weyl group is the Weyl group of an affine Kac–Moody algebra. One may define a Weyl group for an arbitrary Kac–Moody algebra.
The Weyl group as an abstract group is a Coxeter group.
Weyl groups play an important role in representation theory (see Character formula).
References
| [a1] | J. Tits, "Reductive groups over local fields" A. Borel (ed.) W. Casselman (ed.) , Automorphic forms, representations and 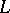 -functions , Proc. Symp. Pure Math. , 33:1 , Amer. Math. Soc. (1979) pp. 29–69 -functions , Proc. Symp. Pure Math. , 33:1 , Amer. Math. Soc. (1979) pp. 29–69 |
| [a2] | J.E. Humphreys, "Reflection groups and Coxeter groups" , Cambridge Univ. Press (1991) |
The Weyl group of a connected compact Lie group 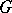 is the quotient group
is the quotient group 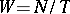 , where
, where 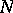 is the normalizer in
is the normalizer in 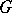 of a maximal torus
of a maximal torus 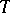 of
of 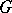 . This Weyl group is isomorphic to a finite group of linear transformations of the Lie algebra
. This Weyl group is isomorphic to a finite group of linear transformations of the Lie algebra 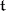 of
of 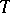 (the isomorphism is realized by the adjoint representation of
(the isomorphism is realized by the adjoint representation of 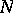 in
in 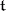 ), and may be characterized with the aid of the root system
), and may be characterized with the aid of the root system 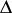 of the Lie algebra
of the Lie algebra 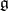 of
of 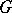 (with respect to
(with respect to 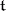 ), as follows: If
), as follows: If  is a system of simple roots of the algebra, which are linear forms on the real vector space
is a system of simple roots of the algebra, which are linear forms on the real vector space 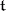 , the Weyl group is generated by the reflections in the hyperplanes
, the Weyl group is generated by the reflections in the hyperplanes  . Thus,
. Thus, 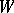 is the Weyl group of the system
is the Weyl group of the system 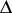 (as a linear group in
(as a linear group in 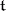 ).
). 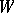 has a simple transitive action on the set of all chambers (cf. Chamber) of
has a simple transitive action on the set of all chambers (cf. Chamber) of 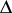 (which, in this case, are referred to as Weyl chambers). It should be noted that, in general,
(which, in this case, are referred to as Weyl chambers). It should be noted that, in general, 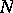 is not the semi-direct product of
is not the semi-direct product of 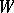 and
and 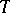 ; all the cases in which it is have been studied. The Weyl group of
; all the cases in which it is have been studied. The Weyl group of 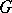 is isomorphic to the Weyl group of the corresponding complex semi-simple algebraic group
is isomorphic to the Weyl group of the corresponding complex semi-simple algebraic group 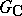 (cf. Complexification of a Lie group).
(cf. Complexification of a Lie group).
A.S. Fedenko
Weyl group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weyl_group&oldid=18086