Vietoris-Begle theorem
One of the most important results in algebraic topology connecting homological (topological) characteristics of topological Hausdorff spaces 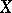 ,
,  (cf. also Hausdorff space) and a continuous mapping
(cf. also Hausdorff space) and a continuous mapping  ; it has applications, for example, in the fixed-point theory for mappings. There are variants of this theorem depending on the choice of the (co)homology functor
; it has applications, for example, in the fixed-point theory for mappings. There are variants of this theorem depending on the choice of the (co)homology functor  (respectively,
(respectively, 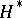 ) when studying homomorphisms
) when studying homomorphisms 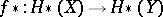 (respectively,
(respectively, 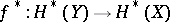 ; see [a1], [a2] and algebraic topology for the necessary constructions and definitions).
; see [a1], [a2] and algebraic topology for the necessary constructions and definitions).
For the functor 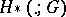 , where
, where 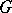 is a group of coefficients, one defines
is a group of coefficients, one defines 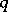 -acyclicity of a set
-acyclicity of a set 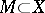 by
by 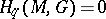 , for
, for 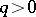 ,
, 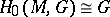 for
for 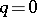 (and similarly for the functor
(and similarly for the functor 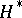 ). If
). If 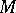 is
is 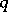 -acyclic for all
-acyclic for all  , then
, then 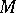 is said to be acyclic.
is said to be acyclic.
The simplest variant of the Vietoris–Begle theorem (close to [a3]) is as follows. Let 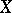 ,
,  be compact Hausdorff spaces, let
be compact Hausdorff spaces, let  be the Aleksandrov–Čech homology functor (over the field
be the Aleksandrov–Čech homology functor (over the field 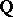 of rational numbers; cf. also Aleksandrov–Čech homology and cohomology), let the mapping of compact pairs
of rational numbers; cf. also Aleksandrov–Čech homology and cohomology), let the mapping of compact pairs 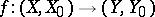 have non-empty acyclic pre-images
have non-empty acyclic pre-images 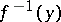 for any
for any 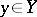 and let
and let 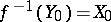 ; then the induced homomorphisms
; then the induced homomorphisms  ,
, 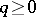 , are isomorphisms (cf. also Homomorphism; Isomorphism). This result is also valid if one drops the condition of compactness of spaces and pairs and replaces it by the condition that
, are isomorphisms (cf. also Homomorphism; Isomorphism). This result is also valid if one drops the condition of compactness of spaces and pairs and replaces it by the condition that 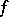 be a proper mapping (cf. also Proper morphism) [a4].
be a proper mapping (cf. also Proper morphism) [a4].
For the Aleksandrov–Kolmogorov functor  in the category of paracompact Hausdorff spaces and a bounded continuous surjective mapping
in the category of paracompact Hausdorff spaces and a bounded continuous surjective mapping 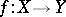 one studies the cohomology homomorphism
one studies the cohomology homomorphism 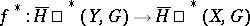 , where
, where 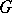 is an
is an 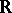 -module. If the pre-image
-module. If the pre-image 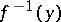 , for any
, for any 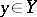 , is
, is 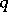 -acyclic for all
-acyclic for all 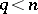 (for a fixed
(for a fixed 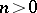 ), then the homomorphism
), then the homomorphism 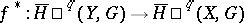 is an isomorphism for
is an isomorphism for 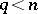 and it is a monomorphism for
and it is a monomorphism for  [a2]. In the case of locally compact spaces
[a2]. In the case of locally compact spaces 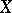 ,
, 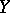 , the statement is valid for cohomologies
, the statement is valid for cohomologies 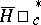 with compact supports under the additional condition that
with compact supports under the additional condition that 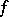 be a proper mapping (cf. also Proper morphism) [a2].
be a proper mapping (cf. also Proper morphism) [a2].
In the case of metric spaces 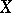 ,
, 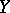 , the requirement that the pre-images
, the requirement that the pre-images 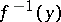 be
be 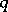 -acyclic at all points
-acyclic at all points 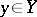 can be weakened in that one allows sets
can be weakened in that one allows sets 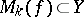 for which the
for which the 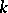 -acyclicity property is broken:
-acyclicity property is broken: 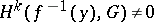 (
(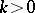 ),
), 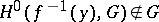 (
(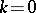 ), where
), where 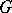 is the group of coefficients. One defines the relative dimension of
is the group of coefficients. One defines the relative dimension of 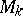 in
in 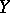 ,
, 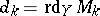 as the supremum of
as the supremum of 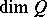 , where
, where 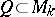 runs over the subsets bounded in
runs over the subsets bounded in  . One defines a "weight measure" of
. One defines a "weight measure" of 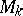 in
in 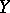 by
by
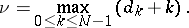 |
If 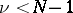 , then the homomorphism
, then the homomorphism 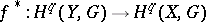 is [a5]:
is [a5]:
for 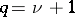 an epimorphism;
an epimorphism;
for 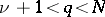 an isomorphism; and
an isomorphism; and
for 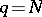 a monomorphism. A mapping
a monomorphism. A mapping 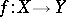 is said to be an
is said to be an  -Vietoris mapping (
-Vietoris mapping (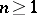 ) if
) if 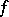 is a proper, surjective and
is a proper, surjective and 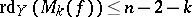 for all
for all 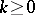 [a4]. From the previous statement it follows that for an
[a4]. From the previous statement it follows that for an  -Vietoris mapping
-Vietoris mapping  the homomorphism
the homomorphism 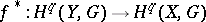 is an isomorphism for
is an isomorphism for 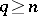 . For a
. For a 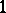 -Vietoris mapping,
-Vietoris mapping, 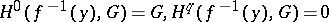 , for all
, for all 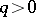 , i.e. all the pre-images
, i.e. all the pre-images 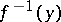 are acyclic; such mappings are called Vietoris mappings.
are acyclic; such mappings are called Vietoris mappings.
Fixed-point theory.
Vietoris–Begle-type theorems are connected with the problem of equality, 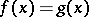 , for some
, for some  , with the problem of coincidence of pairs
, with the problem of coincidence of pairs 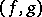 of mappings
of mappings 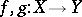 , and with the fixed-point problem for set-valued mappings (see, for example, [a6], [a7], [a8], [a4], [a9], [a10], [a11], [a13]).
, and with the fixed-point problem for set-valued mappings (see, for example, [a6], [a7], [a8], [a4], [a9], [a10], [a11], [a13]).
In fact, the set-valued mapping 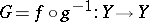 , where
, where 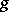 is a surjection, gives a connection between the two problems: a point
is a surjection, gives a connection between the two problems: a point  at which
at which 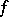 and
and 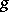 coincide, defines a fixed point
coincide, defines a fixed point 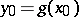 for
for 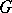 (
(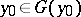 ), and vice versa; in fact, if
), and vice versa; in fact, if 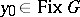 , then
, then 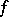 is equal to
is equal to 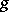 at any point
at any point 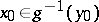 .
.
For general set-valued mappings 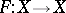 it is easy to construct a corresponding pair: consider the graph of the set-valued mapping
it is easy to construct a corresponding pair: consider the graph of the set-valued mapping 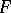 ,
,
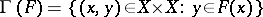 |
and its Cartesian projections 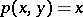 ,
, 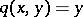 . One obtains the pair
. One obtains the pair 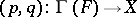 , for which a point of coincidence
, for which a point of coincidence 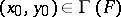 ,
,  , defines a fixed point
, defines a fixed point 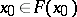 of the set-valued mapping
of the set-valued mapping 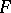 .
.
Topological characteristics.
Topological characteristics such as the Lefschetz number, the Kronecker characteristic, the rotation of the vector field (M.A. Krasnoselskii), the Brouwer–Hopf degree, are well known for single-valued mappings in finite-dimensional spaces (see, for example, [a12]). Analogous characteristics for general set-valued mappings 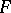 have been constructed on the basis of homomorphisms
have been constructed on the basis of homomorphisms 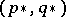 , (respectively,
, (respectively, 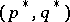 ) of (co)homology groups of the pair
) of (co)homology groups of the pair 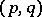 for
for 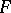 . These set-valued mappings satisfy the general conditions of compactness of images and have the property of upper semi-continuity. However, there is also a homological condition for a mapping
. These set-valued mappings satisfy the general conditions of compactness of images and have the property of upper semi-continuity. However, there is also a homological condition for a mapping 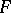 to be
to be  -Vietoris, ensuring an isomorphism
-Vietoris, ensuring an isomorphism  (respectively,
(respectively, 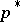 ) in homology (cohomology) of dimension
) in homology (cohomology) of dimension  , and permitting one to construct a homomorphism
, and permitting one to construct a homomorphism 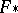 (respectively,
(respectively,  ), generated by the set-valued mapping in (co)homology by the formula
), generated by the set-valued mapping in (co)homology by the formula 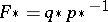 (respectively,
(respectively, 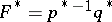 ).
).
S. Eilenberg and D. Montgomery [a6] have generalized the classical construction of the Lefschetz number to set-valued upper semi-continuous mappings 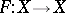 with acyclic images, where
with acyclic images, where 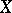 is compact metric ANR-space:
is compact metric ANR-space:
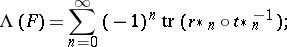 |
here, 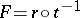 is a canonical decomposition of
is a canonical decomposition of 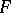 , where
, where 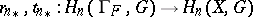 are homomorphisms and
are homomorphisms and 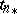 is an isomorphism for any
is an isomorphism for any 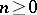 (due to the Vietoris–Begle theorem). If
(due to the Vietoris–Begle theorem). If 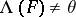 , then
, then 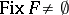 . This result was generalized by many authors (see [a9], [a10], [a4], [a7]). These generalizations involve weaker conditions of acyclicity, as well as certain different variants.
. This result was generalized by many authors (see [a9], [a10], [a4], [a7]). These generalizations involve weaker conditions of acyclicity, as well as certain different variants.
Degree theory.
To describe the topological characteristics of set-valued mappings 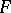 like the degree
like the degree 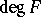 or the Kronecker characteristics
or the Kronecker characteristics 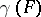 some definitions are needed. Let
some definitions are needed. Let 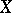 ,
, 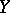 ,
, 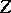 be separable topological spaces (cf. also Separable space), let
be separable topological spaces (cf. also Separable space), let 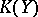 be the space of compact subsets, and suppose the set-valued mapping
be the space of compact subsets, and suppose the set-valued mapping 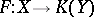 is upper semi-continuous. Such a mapping is called
is upper semi-continuous. Such a mapping is called
 -acyclic if
-acyclic if 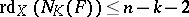 for all
for all 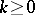 (here,
(here, 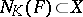 is the set of points
is the set of points  at which the
at which the  -acyclicity of the images
-acyclicity of the images  is broken);
is broken);
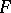 -acyclic if it is
-acyclic if it is 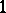 -acyclic; this is equivalent to acyclicity of every image
-acyclic; this is equivalent to acyclicity of every image 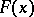 . A mapping
. A mapping  is called generally
is called generally  -acyclic if there exist a space
-acyclic if there exist a space 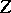 and single-valued continuous mappings
and single-valued continuous mappings  ,
, 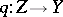 , where
, where 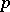 is
is  -Vietoris and
-Vietoris and  for all
for all 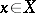 . The collection
. The collection 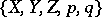 is then said to be a representation of the set-valued mapping
is then said to be a representation of the set-valued mapping 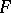 , the pair
, the pair 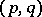 is called a selecting pair, and the mapping
is called a selecting pair, and the mapping 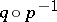 is called a selector of
is called a selector of 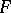 . For an
. For an  -acyclic mapping
-acyclic mapping 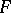 , the projections of the graph
, the projections of the graph 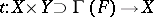 ,
, 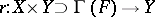 give a selecting pair:
give a selecting pair:
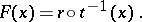 |
As an example, consider the main construction of the degree of a mapping 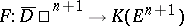 from the unit disc
from the unit disc 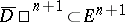 in the Euclidean space
in the Euclidean space 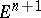 under the condition that
under the condition that 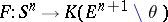 , where
, where 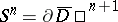 , is
, is 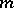 -acyclic,
-acyclic, 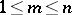 . A generalization of the Vietoris–Begle theorem given by E.G. Sklyarenko ensures the existence of cohomology isomorphisms
. A generalization of the Vietoris–Begle theorem given by E.G. Sklyarenko ensures the existence of cohomology isomorphisms 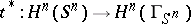 ,
, 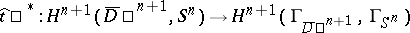 over the group
over the group 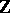 . Then
. Then 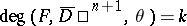 , where
, where 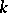 is given by the equality
is given by the equality 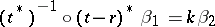 . Here,
. Here, 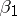 , respectively
, respectively 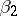 , is a generator of the group
, is a generator of the group 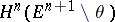 , respectively
, respectively 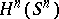 , which is isomorphic to
, which is isomorphic to 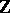 , and
, and 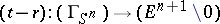 (a construction given by D.G. Bourgin, L. Górniewicz, and others, see [a9], [a10], [a4]). If the mapping
(a construction given by D.G. Bourgin, L. Górniewicz, and others, see [a9], [a10], [a4]). If the mapping  under consideration is generally acyclic, then for every selecting pair
under consideration is generally acyclic, then for every selecting pair 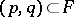 the set-valued mapping (the selector of
the set-valued mapping (the selector of 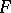 )
) 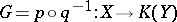 is
is  -acyclic, and for it
-acyclic, and for it 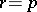 ,
, 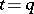 ; applying the previous construction for the selector
; applying the previous construction for the selector 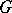 of the set-valued mapping
of the set-valued mapping 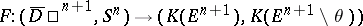 , one obtains
, one obtains  for any selector
for any selector  . The generalized degree
. The generalized degree  is the set
is the set  generated by all selecting pairs
generated by all selecting pairs 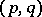 for the
for the  -mapping
-mapping 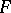 . A more general construction (without the condition that
. A more general construction (without the condition that 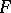 be
be 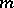 -acyclic) was introduced by B.D. Gelman (see [a10]); namely, the topological characteristic
-acyclic) was introduced by B.D. Gelman (see [a10]); namely, the topological characteristic 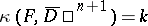 , where
, where 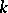 is defined by the equality
is defined by the equality
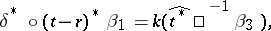 |
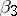 is a generator in
is a generator in 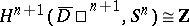 , all the generators
, all the generators 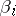 are in accordance with the orientation of
are in accordance with the orientation of 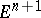 , and
, and 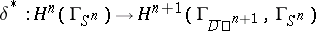 is a connecting homomorphism.
is a connecting homomorphism.
Note that an earlier definition of rotation of a set-valued field 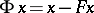 ,
, 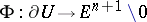 , with non-acyclic images was given in [a8], [a13], [a14].
, with non-acyclic images was given in [a8], [a13], [a14].
References
| [a1] | S. Eilenberg, N. Steenrod, "Foundations of algebraic topology" , Princeton Univ. Press (1952) |
| [a2] | E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) |
| [a3] | E.G. Begle, "The Vietoris mappings theorem for bicompact spaces" Ann. of Math. , 51 : 2 (1950) pp. 534–550 |
| [a4] | L. Górniewicz, "Homological methods in fixed-point theory of multi-valued maps" Dissert. Math. , CXXIX (1976) pp. 1–71 |
| [a5] | E.G. Sklyarenko, "Of some applications of theory of bundles in general topology" Uspekhi Mat. Nauk , 19 : 6 (1964) pp. 47–70 (In Russian) |
| [a6] | S. Eilenberg, D. Montgomery, "Fixed point theorems for multi-valued transformations" Amer. J. Math. , 68 (1946) pp. 214–222 |
| [a7] | A. Granas, J.W. Jaworowski, "Some theorems on multi-valued maps of subsets of the Euclidean space" Bull. Acad. Polon. Sci. , 7 : 5 (1959) pp. 277–283 |
| [a8] | Yu.G. Borisovich, B.D. Gelman, V.V. Obukhovskii, "Of some topological invariants of set-valued maps with nonconvex images" Proc. Sem. Functional Analysis, Voronezh State Univ. , 12 (1969) pp. 85–95 |
| [a9] | Yu.G. Borisovich, B.D. Gelman, A.D. Myshkis, V.V. Obukhovskii, "Topological methods in the fixed-point theory of multi-valued maps" Russian Math. Surveys , 35 : 1 (1980) pp. 65–143 (In Russian) |
| [a10] | Yu.G. Borisovich, B.D. Gelman, A.D. Myshkis, V.V. Obukhovskii, "Multivalued mappings" J. Soviet Math. , 24 (1984) pp. 719–791 (In Russian) |
| [a11] | Yu.G. Borisovich, "A modern appoach to the theory of topological characteristics of nonlinear operators II" , Global analysis: Studies and Applications IV , Lecture Notes Math. , 1453 , Springer (1990) pp. 21–49 |
| [a12] | Yu.G. Borisovich, N.M. Bliznyakov, T.N. Fomenko, Y.A. Izrailevich, "Introduction to differential and algebraic topology" , Kluwer Acad. Publ. (1995) |
| [a13] | L. Górniewicz, "On non-acyclic multi-valued mappings of subsets of Euclidean spaces" Bull. Acad. Polon. Sci. , 20 : 5 (1972) pp. 379–385 |
| [a14] | D.G. Bouvgin, "Cones and Vietoris–Begle type theorems" Trans. Amer. Math. Soc. , 174 (1972) pp. 155–183 |
Vietoris-Begle theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Vietoris-Begle_theorem&oldid=15219