User:Jjtorrens/BancoDePruebas
2020 Mathematics Subject Classification: Primary: 46E35 [MSN][ZBL]
$\newcommand{\abs}[1]{\lvert #1\rvert}
\newcommand{\norm}[1]{\lVert #1\rVert}
\newcommand{\bfl}{\mathbf{l}}$
A locally summable generalized derivative of a locally summable function (see Generalized function).
More explicitly, if  is an open set in an
is an open set in an  -dimensional space
-dimensional space 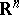 and if
and if  and
and  are locally summable functions on
are locally summable functions on  , then
, then 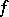 is the Sobolev generalized partial derivative with respect to
is the Sobolev generalized partial derivative with respect to 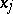 of
of 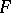 on
on  :
:
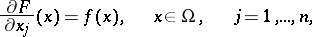 |
if the following equation holds:
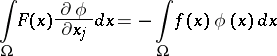 |
for all infinitely-differentiable functions 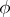 on
on  with compact support. The Sobolev generalized derivative is only defined almost-everywhere on
with compact support. The Sobolev generalized derivative is only defined almost-everywhere on  .
.
An equivalent definition is as follows: Suppose that a locally summable function 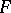 on
on  can be modified in such a way that, on a set of
can be modified in such a way that, on a set of  -dimensional measure zero, it will be locally absolutely continuous with respect to
-dimensional measure zero, it will be locally absolutely continuous with respect to 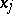 for almost-all points
for almost-all points 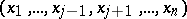 , in the sense of the
, in the sense of the 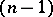 -dimensional measure. Then
-dimensional measure. Then 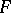 has an ordinary partial derivative with respect to
has an ordinary partial derivative with respect to 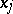 for almost-all
for almost-all 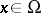 . If the latter is locally summable, then it is called a Sobolev generalized derivative.
. If the latter is locally summable, then it is called a Sobolev generalized derivative.
A third equivalent definition is as follows: Given two functions 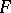 and
and 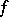 , suppose there is a sequence
, suppose there is a sequence 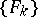 of continuously-differentiable functions on
of continuously-differentiable functions on  such that for any domain
such that for any domain 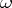 whose closure lies in
whose closure lies in  ,
,
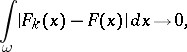 |
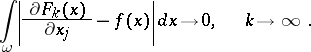 |
Then 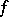 is the Sobolev generalized derivative of
is the Sobolev generalized derivative of 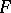 on
on  .
.
Sobolev generalized derivatives of 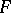 on
on  of higher orders (if they exist) are defined inductively:
of higher orders (if they exist) are defined inductively:
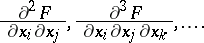 |
They do not depend on the order of differentiation; e.g.,
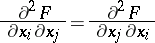 |
almost-everywhere on  .
.
References
| [1] | S.L. Sobolev, "Some applications of functional analysis in mathematical physics" , Amer. Math. Soc. (1963) (Translated from Russian) |
| [2] | S.M. Nikol'skii, "A course of mathematical analysis" , 2 , MIR (1977) (Translated from Russian) |
Comments
In the Western literature the Sobolev generalized derivative is called the weak or distributional derivative.
References
| [a1] | L. Schwartz, "Théorie des distributions" , 1–2 , Hermann (1973) |
| [a2] | K. Yosida, "Functional analysis" , Springer (1980) pp. Chapt. 8, Sect. 4; 5 |
Jjtorrens/BancoDePruebas. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Jjtorrens/BancoDePruebas&oldid=26003