Difference between revisions of "Ultrafilter"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| (One intermediate revision by one other user not shown) | |||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | u0950201.png | ||
| + | $#A+1 = 102 n = 2 | ||
| + | $#C+1 = 102 : ~/encyclopedia/old_files/data/U095/U.0905020 Ultrafilter | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
A [[Filter|filter]] which is maximal, in the sense that every filter containing it coincides with it. An ultrafilter may be defined as a system of subsets satisfying three conditions: 1) the empty set is not included; 2) the intersection of two subsets in the system again belongs to it; and 3) for any subset, either it or its complement belongs to the system. | A [[Filter|filter]] which is maximal, in the sense that every filter containing it coincides with it. An ultrafilter may be defined as a system of subsets satisfying three conditions: 1) the empty set is not included; 2) the intersection of two subsets in the system again belongs to it; and 3) for any subset, either it or its complement belongs to the system. | ||
| Line 7: | Line 19: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> N. Bourbaki, "General topology" , ''Elements of mathematics'' , Springer (1989) pp. Chapts. 1–2 (Translated from French)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> K. Kuratowski, A. Mostowski, "Set theory" , North-Holland (1968)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> N. Bourbaki, "General topology" , ''Elements of mathematics'' , Springer (1989) pp. Chapts. 1–2 (Translated from French)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> K. Kuratowski, A. Mostowski, "Set theory" , North-Holland (1968)</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | Ultrafilters support a considerable body of theory both in general topology and in mathematical logic. For a topologist, they are primarily the elements of free compact spaces — that is, of the Stone–Čech compactifications (cf. [[Stone–Čech compactification|Stone–Čech compactification]]) | + | Ultrafilters support a considerable body of theory both in general topology and in mathematical logic. For a topologist, they are primarily the elements of free compact spaces — that is, of the Stone–Čech compactifications (cf. [[Stone–Čech compactification|Stone–Čech compactification]]) $ \beta D $ |
| + | of discrete spaces $ D $. | ||
| + | $ \beta D $ | ||
| + | is a free compact Hausdorff space on the set $ D $ | ||
| + | of generators, just like a free group on a set of generators; the defining characteristic is that every mapping $ f $ | ||
| + | from the set $ D $ | ||
| + | to a compact Hausdorff space $ X $ | ||
| + | extends uniquely to a continuous mapping $ \beta f : \beta D \rightarrow X $. | ||
| − | To see that free ultrafilters are hard to describe, consider the mapping that assigns to each subset | + | To see that free ultrafilters are hard to describe, consider the mapping that assigns to each subset $ A $ |
| + | of $ \mathbf N $ | ||
| + | the number $ x _ {A} = \sum _ {n \in A } 2 ^ {-} n $ | ||
| + | in the interval $ [ 0, 1 ] $. | ||
| + | If $ u $ | ||
| + | is a free ultrafilter on $ \mathbf N $, | ||
| + | then the set $ \{ {x _ {A} } : {A \in u } \} $ | ||
| + | is non-measurable. | ||
| − | For a logician, ultrafilters are primarily the indexing structures over which ultraproducts are formed. A number of simple but important existential results in model theory are proved in a rather uniform way: To get a model for an infinite set of sentences | + | For a logician, ultrafilters are primarily the indexing structures over which ultraproducts are formed. A number of simple but important existential results in model theory are proved in a rather uniform way: To get a model for an infinite set of sentences $ S $, |
| + | form models for arbitrarily large finite subsets of $ S $( | ||
| + | which is often easy to prove possible) and take any ultraproduct of them. For more control of the construction, one uses restricted ultrafilters, for instance good ultrafilters, or uniform ultrafilters; see [[#References|[a1]]]. | ||
For a discussion of models of set theory without free ultrafilters see [[#References|[a8]]]. | For a discussion of models of set theory without free ultrafilters see [[#References|[a8]]]. | ||
| − | There are two important partial orderings of isomorphism types of ultrafilters on a set, both originating in : the Rudin–Keisler order, defined over an arbitrary set | + | There are two important partial orderings of isomorphism types of ultrafilters on a set, both originating in : the Rudin–Keisler order, defined over an arbitrary set $ D $, |
| + | and the Rudin–Frolik order, defined only over a countable set $ \omega $. | ||
| + | Two ultrafilters $ p, q $ | ||
| + | on $ D $, | ||
| + | i.e. two points of $ \beta D $, | ||
| + | are related by $ p \leq q $ | ||
| + | in the Rudin–Keisler order if there is a mapping $ f : D \rightarrow D \subset \beta D $ | ||
| + | such that $ \beta f( q) = p $. | ||
| + | If $ p \leq q $ | ||
| + | and $ q \leq p $, | ||
| + | $ p $ | ||
| + | and $ q $ | ||
| + | are said to be of the same type. The relation $ p \leq q $ | ||
| + | induces a partial ordering of the types. The Rudin–Frolik order over $ \omega $ | ||
| + | is defined similarly, but using $ f: \omega \rightarrow \beta \omega $ | ||
| + | with discrete image. | ||
| − | [[#References|[a1]]] is a rather full topologically oriented treatment of ultrafilter theory as of 1974, and still the best introduction to the subject. It has a | + | [[#References|[a1]]] is a rather full topologically oriented treatment of ultrafilter theory as of 1974, and still the best introduction to the subject. It has a $ 40 $- |
| + | page chapter on large cardinals, a subject which has had near-revolutionary growth since 1974. | ||
| − | Let | + | Let $ \Phi $ |
| + | be an ultrafilter on an index set $ I $. | ||
| + | For each $ i $, | ||
| + | let $ A _ {i} $ | ||
| + | be a set. Using $ \Phi $ | ||
| + | one defines an equivalence relation on $ \prod A _ {i} $ | ||
| + | as follows: $ a = ( a ( i) ) _ {i \in I } $, | ||
| + | $ b = ( b ( i) ) _ {i \in I } $, | ||
| + | are equivalent if and only if $ \{ {i } : {a( i) = b( i) } \} \in \Phi $( | ||
| + | written: $ a \equiv b $). | ||
| + | The quotient $ ( \prod A _ {i} ) / \Phi $ | ||
| + | of $ \prod A _ {i} $ | ||
| + | by this equivalence relation is called the ultraproduct of the $ A _ {i} $( | ||
| + | with respect to the ultrafilter $ \Phi $). | ||
| − | For each | + | For each $ i $, |
| + | let $ R _ {i} $ | ||
| + | be an $ n $- | ||
| + | ary relation on $ A _ {i} $( | ||
| + | eventually corresponding to one and the same predicate of a language $ L $, | ||
| + | where the $ ( A _ {i} , \{ R _ {i} \} ) $ | ||
| + | are supposed to be interpretations of $ L $). | ||
| + | Then a corresponding relation $ R $ | ||
| + | on $ ( \prod A _ {i} )/ \Phi $ | ||
| + | is defined by: | ||
| − | + | $$ | |
| + | ( \overline{a}\; {} _ {1} \dots \overline{a}\; {} _ {n} ) \in R \iff \ | ||
| + | \{ {i } : {( a _ {1} ( i) \dots a _ {n} ( i) ) \in R _ {i} } \} | ||
| + | \in \Phi . | ||
| + | $$ | ||
| − | Here | + | Here $ \overline{a}\; {} _ {m} $ |
| + | is the equivalence class of $ a _ {m} $ | ||
| + | in $ ( \prod A _ {i} ) / \Phi $. | ||
| + | (This is well defined by the properties of ultrafilters.) Functions and individual constants are similarly defined. | ||
| − | If all the | + | If all the $ A _ {i} $ |
| + | are the same, one speaks of ultrapowers instead of ultraproducts. | ||
| − | Ultraproducts have important applications in the theory of [[Diophantine equations|Diophantine equations]] and [[Algebraic number theory|algebraic number theory]]. For instance, for each prime number | + | Ultraproducts have important applications in the theory of [[Diophantine equations|Diophantine equations]] and [[Algebraic number theory|algebraic number theory]]. For instance, for each prime number $ p $, |
| + | let $ \mathbf Q _ {p} $ | ||
| + | be the field of $ p $- | ||
| + | adic numbers and let $ \mathbf F _ {p} (( t)) $ | ||
| + | be the field of Laurent series over the finite field $ \mathbf F _ {p} = \{ 0 \dots p - 1 \} $. | ||
| + | Then the Ax–Kochen theorem says that for each non-principal ultrafilter $ \Phi $, | ||
| − | + | $$ | |
| + | \prod _ { p } \mathbf Q _ {p} / \Phi \simeq \prod _ { p } | ||
| + | \mathbf F _ {p} (( t)) / \Phi . | ||
| + | $$ | ||
| − | This gives an immediate positive partial solution to Artin's conjecture on Diophantine equations in the form of the theorem: For each positive integer | + | This gives an immediate positive partial solution to Artin's conjecture on Diophantine equations in the form of the theorem: For each positive integer $ d $ |
| + | there exists a finite set of primes $ P( d) $ | ||
| + | such that every homogeneous polynomial $ f ( X _ {1} \dots X _ {n} ) $ | ||
| + | of degree $ d $ | ||
| + | over $ \mathbf Q _ {p} $ | ||
| + | with $ n > d ^ {2} $ | ||
| + | has a non-trivial zero in $ \mathbf Q _ {p} $ | ||
| + | for all $ p \notin P( d) $. | ||
| + | This result can also be deduced from results of Yu.L. Ershov ([[#References|[a6]]]), which also use ultraproducts in their proof. Artin's conjecture in full generality says that $ \mathbf Q _ {p} $ | ||
| + | is a $ C _ {2} $- | ||
| + | field, which means that the conclusion just formulated must hold for all $ p $( | ||
| + | the "2" in $ C _ {2} $- | ||
| + | field refers to the "2" in "n>d2" ). However, G. Terjanian gave in 1966 a counterexample to the full Artin conjecture by providing a quartic form in $ 18 $ | ||
| + | variables over $ \mathbf Q _ {2} $ | ||
| + | with only non-trivial zeros. | ||
| − | More precisely, let | + | More precisely, let $ i \geq 0 $, |
| + | $ d \geq 1 $ | ||
| + | be integers. Then a field $ F $ | ||
| + | is called a $ C _ {i} ( d) $- | ||
| + | field if every homogeneous polynomial $ f( X _ {1} \dots X _ {n} ) $ | ||
| + | of degree $ d $ | ||
| + | over $ F $ | ||
| + | in $ n > d ^ {i} $ | ||
| + | variables has a non-trivial zero in $ F $. | ||
| + | A field that is $ C _ {i} ( d) $ | ||
| + | for all $ d \geq 1 $ | ||
| + | is called a $ C _ {i} $- | ||
| + | field. The $ C _ {0} $- | ||
| + | fields are the algebraically closed fields. The $ C _ {1} $- | ||
| + | fields are also called quasi-algebraically closed. The rational functions in one variable over an algebraically closed field form a $ C _ {1} $- | ||
| + | field ([[Tsen's theorem]]). The field $ \mathbf Q _ {p} $ | ||
| + | is a $ C _ {2} ( 2) $- | ||
| + | field (H. Hasse, 1923) and also a $ C _ {2} ( 3) $- | ||
| + | field (D.J. Lewis, 1952). | ||
| − | Other important applications of ultraproducts are in [[Non-standard analysis|non-standard analysis]]; in particular, non-standard models of the reals, integers, etc. can be obtained as ultrapowers of | + | Other important applications of ultraproducts are in [[Non-standard analysis|non-standard analysis]]; in particular, non-standard models of the reals, integers, etc. can be obtained as ultrapowers of $ \mathbf R $, |
| + | $ \mathbf Z $, | ||
| + | etc. | ||
Cf. [[Model theory|Model theory]] and [[#References|[a2]]] for results in logic involving ultrafilters and ultraproducts. | Cf. [[Model theory|Model theory]] and [[#References|[a2]]] for results in logic involving ultrafilters and ultraproducts. | ||
Revision as of 08:27, 6 June 2020
A filter which is maximal, in the sense that every filter containing it coincides with it. An ultrafilter may be defined as a system of subsets satisfying three conditions: 1) the empty set is not included; 2) the intersection of two subsets in the system again belongs to it; and 3) for any subset, either it or its complement belongs to the system.
All ultrafilters are divided into two classes: trivial (or fixed or principal) and free ultrafilters. An ultrafilter is called trivial or principal if it is the system of all subsets containing a given point; such an ultrafilter is also called fixed in that point. An ultrafilter is called free if the intersection of all its elements is the empty set, in other words, if it is not fixed in any point. The existence of free ultrafilters is unprovable without the axiom of choice.
For every filter there is an ultrafilter containing it; moreover, every filter is precisely the intersection of all the ultrafilters containing it.
References
| [1] | N. Bourbaki, "General topology" , Elements of mathematics , Springer (1989) pp. Chapts. 1–2 (Translated from French) |
| [2] | K. Kuratowski, A. Mostowski, "Set theory" , North-Holland (1968) |
Comments
Ultrafilters support a considerable body of theory both in general topology and in mathematical logic. For a topologist, they are primarily the elements of free compact spaces — that is, of the Stone–Čech compactifications (cf. Stone–Čech compactification) $ \beta D $ of discrete spaces $ D $. $ \beta D $ is a free compact Hausdorff space on the set $ D $ of generators, just like a free group on a set of generators; the defining characteristic is that every mapping $ f $ from the set $ D $ to a compact Hausdorff space $ X $ extends uniquely to a continuous mapping $ \beta f : \beta D \rightarrow X $.
To see that free ultrafilters are hard to describe, consider the mapping that assigns to each subset $ A $ of $ \mathbf N $ the number $ x _ {A} = \sum _ {n \in A } 2 ^ {-} n $ in the interval $ [ 0, 1 ] $. If $ u $ is a free ultrafilter on $ \mathbf N $, then the set $ \{ {x _ {A} } : {A \in u } \} $ is non-measurable.
For a logician, ultrafilters are primarily the indexing structures over which ultraproducts are formed. A number of simple but important existential results in model theory are proved in a rather uniform way: To get a model for an infinite set of sentences $ S $, form models for arbitrarily large finite subsets of $ S $( which is often easy to prove possible) and take any ultraproduct of them. For more control of the construction, one uses restricted ultrafilters, for instance good ultrafilters, or uniform ultrafilters; see [a1].
For a discussion of models of set theory without free ultrafilters see [a8].
There are two important partial orderings of isomorphism types of ultrafilters on a set, both originating in : the Rudin–Keisler order, defined over an arbitrary set $ D $, and the Rudin–Frolik order, defined only over a countable set $ \omega $. Two ultrafilters $ p, q $ on $ D $, i.e. two points of $ \beta D $, are related by $ p \leq q $ in the Rudin–Keisler order if there is a mapping $ f : D \rightarrow D \subset \beta D $ such that $ \beta f( q) = p $. If $ p \leq q $ and $ q \leq p $, $ p $ and $ q $ are said to be of the same type. The relation $ p \leq q $ induces a partial ordering of the types. The Rudin–Frolik order over $ \omega $ is defined similarly, but using $ f: \omega \rightarrow \beta \omega $ with discrete image.
[a1] is a rather full topologically oriented treatment of ultrafilter theory as of 1974, and still the best introduction to the subject. It has a $ 40 $- page chapter on large cardinals, a subject which has had near-revolutionary growth since 1974.
Let $ \Phi $ be an ultrafilter on an index set $ I $. For each $ i $, let $ A _ {i} $ be a set. Using $ \Phi $ one defines an equivalence relation on $ \prod A _ {i} $ as follows: $ a = ( a ( i) ) _ {i \in I } $, $ b = ( b ( i) ) _ {i \in I } $, are equivalent if and only if $ \{ {i } : {a( i) = b( i) } \} \in \Phi $( written: $ a \equiv b $). The quotient $ ( \prod A _ {i} ) / \Phi $ of $ \prod A _ {i} $ by this equivalence relation is called the ultraproduct of the $ A _ {i} $( with respect to the ultrafilter $ \Phi $).
For each $ i $, let $ R _ {i} $ be an $ n $- ary relation on $ A _ {i} $( eventually corresponding to one and the same predicate of a language $ L $, where the $ ( A _ {i} , \{ R _ {i} \} ) $ are supposed to be interpretations of $ L $). Then a corresponding relation $ R $ on $ ( \prod A _ {i} )/ \Phi $ is defined by:
$$ ( \overline{a}\; {} _ {1} \dots \overline{a}\; {} _ {n} ) \in R \iff \ \{ {i } : {( a _ {1} ( i) \dots a _ {n} ( i) ) \in R _ {i} } \} \in \Phi . $$
Here $ \overline{a}\; {} _ {m} $ is the equivalence class of $ a _ {m} $ in $ ( \prod A _ {i} ) / \Phi $. (This is well defined by the properties of ultrafilters.) Functions and individual constants are similarly defined.
If all the $ A _ {i} $ are the same, one speaks of ultrapowers instead of ultraproducts.
Ultraproducts have important applications in the theory of Diophantine equations and algebraic number theory. For instance, for each prime number $ p $, let $ \mathbf Q _ {p} $ be the field of $ p $- adic numbers and let $ \mathbf F _ {p} (( t)) $ be the field of Laurent series over the finite field $ \mathbf F _ {p} = \{ 0 \dots p - 1 \} $. Then the Ax–Kochen theorem says that for each non-principal ultrafilter $ \Phi $,
$$ \prod _ { p } \mathbf Q _ {p} / \Phi \simeq \prod _ { p } \mathbf F _ {p} (( t)) / \Phi . $$
This gives an immediate positive partial solution to Artin's conjecture on Diophantine equations in the form of the theorem: For each positive integer $ d $ there exists a finite set of primes $ P( d) $ such that every homogeneous polynomial $ f ( X _ {1} \dots X _ {n} ) $ of degree $ d $ over $ \mathbf Q _ {p} $ with $ n > d ^ {2} $ has a non-trivial zero in $ \mathbf Q _ {p} $ for all $ p \notin P( d) $. This result can also be deduced from results of Yu.L. Ershov ([a6]), which also use ultraproducts in their proof. Artin's conjecture in full generality says that $ \mathbf Q _ {p} $ is a $ C _ {2} $- field, which means that the conclusion just formulated must hold for all $ p $( the "2" in $ C _ {2} $- field refers to the "2" in "n>d2" ). However, G. Terjanian gave in 1966 a counterexample to the full Artin conjecture by providing a quartic form in $ 18 $ variables over $ \mathbf Q _ {2} $ with only non-trivial zeros.
More precisely, let $ i \geq 0 $, $ d \geq 1 $ be integers. Then a field $ F $ is called a $ C _ {i} ( d) $- field if every homogeneous polynomial $ f( X _ {1} \dots X _ {n} ) $ of degree $ d $ over $ F $ in $ n > d ^ {i} $ variables has a non-trivial zero in $ F $. A field that is $ C _ {i} ( d) $ for all $ d \geq 1 $ is called a $ C _ {i} $- field. The $ C _ {0} $- fields are the algebraically closed fields. The $ C _ {1} $- fields are also called quasi-algebraically closed. The rational functions in one variable over an algebraically closed field form a $ C _ {1} $- field (Tsen's theorem). The field $ \mathbf Q _ {p} $ is a $ C _ {2} ( 2) $- field (H. Hasse, 1923) and also a $ C _ {2} ( 3) $- field (D.J. Lewis, 1952).
Other important applications of ultraproducts are in non-standard analysis; in particular, non-standard models of the reals, integers, etc. can be obtained as ultrapowers of $ \mathbf R $, $ \mathbf Z $, etc.
Cf. Model theory and [a2] for results in logic involving ultrafilters and ultraproducts.
There are further important applications of ultrafilters to topology, cf. [a1], [a7].
References
| [a1] | W.W. Comfort, S. Negrepontis, "The theory of ultrafilters" , Springer (1974) |
| [a2] | J.L. Bell, A.B. Slomson, "Models and ultraproducts" , North-Holland (1969) |
| [a3] | J. Ax, S. Kochen, "Diophantine problems over local fields I" Amer. J. Math. , 87 (1965) pp. 605–630 |
| [a4] | J. Ax, S. Kochen, "Diophantine problems over local fields II. A complete set of axioms for 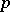 -adic number theory" Amer. J. Math. , 87 (1965) pp. 631–648 -adic number theory" Amer. J. Math. , 87 (1965) pp. 631–648 |
| [a5] | J. Ax, S. Kochen, "Diophantine problems over local fields III. Decidable fields" Ann. of Math. , 83 (1966) pp. 437–456 |
| [a6] | Yu.L. Ershov, "On the elementary theory of maximal normal fields" Soviet Math. Dokl. , 6 (1965) pp. 1390–1393 Dokl. Akad. Nauk SSSR , 165 (1965) pp. 21–23 |
| [a7] | A.V. Arkhangel'skii, V.I. Ponomarev, "Fundamentals of general topology: problems and exercises" , Reidel (1984) (Translated from Russian) |
| [a8] | T.J. Jech, "Set theory" , Acad. Press (1978) pp. 523ff (Translated from German) |
| [a9] | J. van Mill, "An introduction to 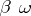 " K. Kunen (ed.) J.E. Vaughan (ed.) , Handbook of Set-Theoretic Topology , North-Holland (1984) " K. Kunen (ed.) J.E. Vaughan (ed.) , Handbook of Set-Theoretic Topology , North-Holland (1984) |
| [a10] | W. Rudin, "Homogeneity problems in the theory of Čech compactification" Duke Math. J. , 23 (1956) pp. 409–419 |
Ultrafilter. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ultrafilter&oldid=18223