Two-person zero-sum game
A game played by two opponents with strictly opposite interests. This means, formally, that on passing from one game situation to another, an increase in the pay-off of one player results in a numerically equal decrease in the pay-off of the other, so that in any situation the sum of the pay-offs of the players is constant (this sum may be considered as zero, since the pay-off of one player is equal to the loss of the other). For this reason two-person zero-sum games are also called two-person games with zero sum, or antagonistic games. The mathematical concept of a two-person zero-sum game — pay-off functions which are numerically equal and opposite in sign — is a formal concept, which differs from the corresponding philosophical concept. If, in a two-person zero-sum game, one of the players manages to increase his pay-off by a definite amount of money as a result of agreements and negotiations, his opponent will have lost an equal sum. Consequently, any agreement would be disadvantageous to one of the players, and therefore impossible. Real conflict situations, which may be adequately modelled by two-person zero-sum games, are some (but not all) military operations, sport matches and parlour games, as well as situations which involve bilateral decision making under strict competition. Games played against nature and, in general, decision making under uncertainty conditions (cf. Statistical game) may be regarded as two-person zero-sum games if it is assumed that the real laws of nature, which are unknown to the player, will produce effects least favourable to the player.
The definition of a two-person zero-sum game in normal form (cf. Games, theory of) amounts to defining sets of strategies  and
and  of players I and II respectively, and of the pay-off function
of players I and II respectively, and of the pay-off function  of player I, defined on the set
of player I, defined on the set  of all situations (the pay-off function of player II is
of all situations (the pay-off function of player II is  by definition). Formally, a two-person zero-sum game
by definition). Formally, a two-person zero-sum game  is given by a triplet
is given by a triplet  . Play consists in the players choosing their strategies
. Play consists in the players choosing their strategies  ,
,  , after which player I obtains the sum
, after which player I obtains the sum  from player II. Such a definition of a two-person zero-sum game is sufficiently general to include all variants of two-person zero-sum games, including dynamic games (cf. Dynamic game), differential games and positional games (cf. Positional game), provided that the sets of strategies and the pay-off function are properly described. A rational choice of actions (strategies) of the players in the course of a two-person zero-sum game is based on a minimax principle: If
from player II. Such a definition of a two-person zero-sum game is sufficiently general to include all variants of two-person zero-sum games, including dynamic games (cf. Dynamic game), differential games and positional games (cf. Positional game), provided that the sets of strategies and the pay-off function are properly described. A rational choice of actions (strategies) of the players in the course of a two-person zero-sum game is based on a minimax principle: If
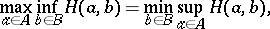 | (1) |
or
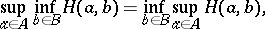 | (1prm) |
the game  has optimal strategies (
has optimal strategies ( -optimal strategies, respectively) for both players (cf. Strategy (in game theory)). The common value of both parts of equation (1prm) is called the value of the game
-optimal strategies, respectively) for both players (cf. Strategy (in game theory)). The common value of both parts of equation (1prm) is called the value of the game 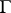 . However, equations (1) or (1prm) may not be valid even in the simplest cases. For example, in a matrix game with pay-off matrix
. However, equations (1) or (1prm) may not be valid even in the simplest cases. For example, in a matrix game with pay-off matrix
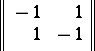 |
the following equalities are valid:
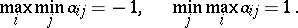 |
For this reason the sets of players' strategies are extended to a set of mixed strategies, which consists in a random choice of initial ( "pure" ) strategies by the players while the pay-off function is defined as the mathematical expectation of the pay-off under conditions of application of the mixed strategies. In the above example, the optimal mixed strategies of both players are the choices of the two strategies with probabilities  , the value of the game in the mixed strategies being zero. If the sets
, the value of the game in the mixed strategies being zero. If the sets  and
and 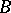 are finite, the two-person zero-sum game is called a matrix game, for which the value of the game and optimal mixed strategies of each player exist in all cases. If both sets
are finite, the two-person zero-sum game is called a matrix game, for which the value of the game and optimal mixed strategies of each player exist in all cases. If both sets  and
and 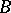 are infinite, optimal (and even
are infinite, optimal (and even  -optimal) strategies can fail to exist (cf. Infinite game).
-optimal) strategies can fail to exist (cf. Infinite game).
References
| [1] | S. Karlin, "Mathematical methods and theory in games, programming and economics" , Addison-Wesley (1959) |
| [2] | T. Parthasarathy, T.L. Raghavan, "Some topics in two-person games" , Elsevier (1971) |
Comments
References
| [a1] | N.H. Vorob'ev, "Game theory. Lectures for economists and system scientists" , Springer (1977) (Translated from Russian) |
| [a2] | G. Owen, "Game theory" , Acad. Press (1982) |
Two-person zero-sum game. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Two-person_zero-sum_game&oldid=15390