Tubular neighbourhood
A neighbourhood of a smooth submanifold 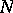 in a smooth manifold
in a smooth manifold 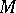 that is fibred over
that is fibred over  with fibre
with fibre 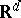 , where
, where
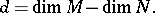 |
Suppose that in 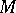 a Riemannian metric is chosen and consider segments of geodesics that are normal to
a Riemannian metric is chosen and consider segments of geodesics that are normal to 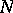 and start in
and start in 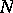 . If
. If 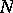 is compact, then there exists an
is compact, then there exists an 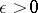 such that no two segments of length
such that no two segments of length 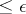 and starting at different points of
and starting at different points of 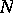 intersect. The union of all such segments of length
intersect. The union of all such segments of length 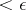 is an open neighbourhood
is an open neighbourhood 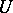 of
of 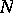 , and is called a tubular neighbourhood of
, and is called a tubular neighbourhood of 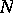 . It is possible to construct for a non-compact
. It is possible to construct for a non-compact 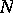 a tubular neighbourhood by covering
a tubular neighbourhood by covering 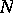 with a countable family of compacta and by decreasing
with a countable family of compacta and by decreasing  as the number of elements of the covering increases. There is a deformation retract
as the number of elements of the covering increases. There is a deformation retract 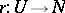 associating with each point of
associating with each point of 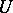 the beginning of a geodesic containing this point. This retract determines a vector bundle with fibre
the beginning of a geodesic containing this point. This retract determines a vector bundle with fibre 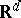 that is isomorphic to the normal bundle
that is isomorphic to the normal bundle  of the imbedding
of the imbedding 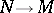 . In this way, the quotient space
. In this way, the quotient space 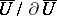 is homeomorphic to the Thom space of
is homeomorphic to the Thom space of  .
.
An analogue of the notion of a tubular neighbourhood can also be introduced for topological manifolds (where one has to consider locally flat imbeddings, [2]).
References
| [1] | R. Thom, "Quelques propriétés globales des variétés différentiables" Comm. Math. Helv. , 28 (1954) pp. 17–86 |
| [2] | R.C. Kirby, L.C. Siebenmann, "Foundational essays on topological manifolds, smoothings, and triangulations" , Princeton Univ. Press (1977) |
Comments
Tubular neighbourhoods were introduced by H. Whitney in his treatment of differentiable manifolds (see [a2] for some history).
References
| [a1] | M.W. Hirsch, "Differential topology" , Springer (1976) pp. Chapt. 5, Sect. 3 |
| [a2] | J. Dieudonné, "A history of algebraic and differential topology: 1900–1960" , Birkhäuser (1989) pp. Chapt. III |
Tubular neighbourhood. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tubular_neighbourhood&oldid=15283