Transposed matrix
From Encyclopedia of Mathematics
The matrix obtained from a given (rectangular or square) matrix 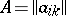 (
(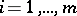 ;
; 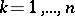 ) by interchanging the rows and the columns, that is, the matrix
) by interchanging the rows and the columns, that is, the matrix 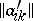 , where
, where 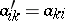 (
(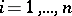 ;
;  ). The number of rows of the transposed matrix is equal to the number of columns of
). The number of rows of the transposed matrix is equal to the number of columns of 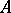 , while the number of columns is equal to the number of rows of
, while the number of columns is equal to the number of rows of 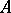 . The transpose of a matrix
. The transpose of a matrix 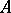 is usually denoted by
is usually denoted by 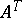 or
or 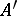 .
.
Comments
Some elementary properties of the transposition of matrices are 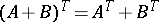 ,
, 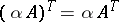 ,
, 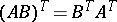 ,
, 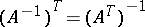 .
.
References
| [a1] | F.R. [F.R. Gantmakher] Gantmacher, "The theory of matrices" , 1 , Chelsea, reprint (1959) pp. 19 (Translated from Russian) |
How to Cite This Entry:
Transposed matrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Transposed_matrix&oldid=15848
Transposed matrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Transposed_matrix&oldid=15848
This article was adapted from an original article by O.A. Ivanova (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article