Thue-Mahler equation
Let 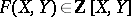 be a binary form of degree
be a binary form of degree 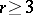 , irreducible over
, irreducible over 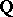 , let
, let 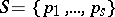 be a fixed set of rational prime numbers and let
be a fixed set of rational prime numbers and let 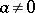 be a fixed rational integer. The Diophantine equation (cf. also Diophantine equations)
be a fixed rational integer. The Diophantine equation (cf. also Diophantine equations)
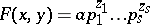 | (a1) |
in the unknowns 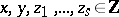 , with
, with  and
and  relatively prime, is called a Thue–Mahler equation. More generally, let
relatively prime, is called a Thue–Mahler equation. More generally, let 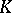 be an algebraic number field (cf. Number field; Algebraic number), let
be an algebraic number field (cf. Number field; Algebraic number), let 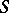 be a fixed finite set of places in
be a fixed finite set of places in 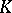 (cf. also Place of a field), containing all infinite ones, let
(cf. also Place of a field), containing all infinite ones, let 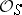 be the ring of
be the ring of 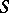 -integers and let
-integers and let 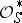 be the group of
be the group of 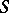 -units of
-units of 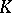 . Let
. Let 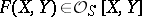 be a binary form of degree
be a binary form of degree 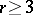 , irreducible over
, irreducible over 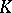 . The Diophantine equation
. The Diophantine equation
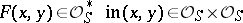 | (a2) |
is called a generalized Thue–Mahler equation. If 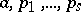 are as in (a1) and one takes in (a2)
are as in (a1) and one takes in (a2) 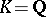 and
and 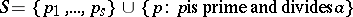 , then all solutions of (a1) are also solutions of (a2). Hence, any result concerning the solutions of (a1) applies also to those of (a2).
, then all solutions of (a1) are also solutions of (a2). Hence, any result concerning the solutions of (a1) applies also to those of (a2).
In 1933, K. Mahler, using his  -adic analogues of the methods of A. Thue [a7] and C.L. Siegel [a5], proved in [a3] that a Thue–Mahler equation (a1) has at most finitely many solutions. Because of the applied methods, this result is non-effective, i.e. it does not imply an explicit bound for either the size of the unknowns, or for the number of solutions. The development of Baker's theory (cf. also Gel'fond–Baker method) and its
-adic analogues of the methods of A. Thue [a7] and C.L. Siegel [a5], proved in [a3] that a Thue–Mahler equation (a1) has at most finitely many solutions. Because of the applied methods, this result is non-effective, i.e. it does not imply an explicit bound for either the size of the unknowns, or for the number of solutions. The development of Baker's theory (cf. also Gel'fond–Baker method) and its  -adic analogues made possible, in the 1970s, the proof of effective, though not explicit, bounds for the size of the unknowns; see [a4], Chap. 7. Subsequently, very explicit upper bounds for
-adic analogues made possible, in the 1970s, the proof of effective, though not explicit, bounds for the size of the unknowns; see [a4], Chap. 7. Subsequently, very explicit upper bounds for
 |
have been proved. A characteristic result of this type is due to Y. Bugeaud and K. Gőry [a1], in which the quantities  ,
,  ,
, 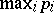 ,
,  ,
, 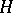 ,
, 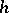 ,
, 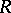 are involved; here,
are involved; here, 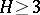 is an upper bound for the absolute values of the coefficients of
is an upper bound for the absolute values of the coefficients of 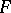 and
and 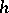 ,
, 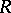 are, respectively, the class number and the regulator of the number field generated (over
are, respectively, the class number and the regulator of the number field generated (over 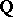 ) by a root of the polynomial
) by a root of the polynomial 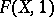 (cf. also Class field theory).
(cf. also Class field theory).
Due to techniques in Diophantine approximations, explicit upper bounds for the number of essentially distinct solutions have been proved for (a2), where two solutions 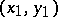 ,
, 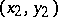 are considered as essentially distinct if
are considered as essentially distinct if 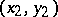 is not of the form
is not of the form 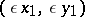 for some
for some 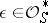 . In view of the observation following (a2), such a bound is also valid for the number of solutions of (a1). Thus, Mahler's finiteness result has been considerably generalized and, what is more, in an explicit form. A characteristic result of this type is due to J.-H. Evertse [a2]: Let the cardinality of
. In view of the observation following (a2), such a bound is also valid for the number of solutions of (a1). Thus, Mahler's finiteness result has been considerably generalized and, what is more, in an explicit form. A characteristic result of this type is due to J.-H. Evertse [a2]: Let the cardinality of 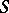 in (a2) be
in (a2) be  . Then, the number of essentially distinct solutions
. Then, the number of essentially distinct solutions 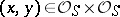 is at most
is at most 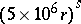 .
.
In the early 1990s, constructive methods for the explicit computation of all solutions of a Thue–Mahler equation (a1) were developed by N. Tzanakis and B.M.M. de Weger [a8], [a9]. These are based on the theory (real and complex as well as 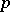 -adic) of linear forms in logarithms of algebraic numbers (cf. Linear form in logarithms) and reduction techniques, like the LLL-basis reduction algorithm and the computation of "small" vectors in a lattice (cf. also LLL basis reduction method). This method can, in principle, be extended to equations of the form (a2), as shown by N.P. Smart in [a6].
-adic) of linear forms in logarithms of algebraic numbers (cf. Linear form in logarithms) and reduction techniques, like the LLL-basis reduction algorithm and the computation of "small" vectors in a lattice (cf. also LLL basis reduction method). This method can, in principle, be extended to equations of the form (a2), as shown by N.P. Smart in [a6].
References
| [a1] | Y. Bugeaud, K. Győry, "Bounds for the solutions of Thue–Mahler equations and norm form equations" Acta Arith. , 74 (1996) pp. 273–292 |
| [a2] | J.-H. Evertse, "The number of solutions of the Thue–Mahler equation" J. Reine Angew. Math. , 482 (1997) pp. 121–149 |
| [a3] | K. Mahler, "Zur Approximation algebraischer Zahlen, I: Ueber den grössten Primteiler binärer Formen" Math. Ann. , 107 (1933) pp. 691–730 |
| [a4] | T.N. Shorey, R. Tijdeman, "Exponential Diophantine equations" , Tracts in Math. , 87 , Cambridge Univ. Press (1986) |
| [a5] | C.L. Siegel, "Approximation algebraischer Zahlen" Math. Z. , 10 (1921) pp. 173–213 |
| [a6] | N.P. Smart, "Thue and Thue–Mahler equations over rings of integers" J. London Math. Soc. , 56 : 2 (1997) pp. 455–462 |
| [a7] | A. Thue, "Ueber Annäherungswerte algebraischer Zahlen" J. Reine Angew. Math. , 135 (1909) pp. 284–305 |
| [a8] | N. Tzanakis, B.M.M. de Weger, "Solving a specific Thue–Mahler equation" Math. Comp. , 57 (1991) pp. 799–815 |
| [a9] | N. Tzanakis, B.M.M. de Weger, "How to explicitly solve a Thue–Mahler equation" Compositio Math. , 84 (1992) pp. 223–288 |
Thue-Mahler equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Thue-Mahler_equation&oldid=18261