Thom-Mather stratification
A stratification of a space such that each stratum has a neighbourhood which fibres over that stratum, with levels defined by a tubular function (called "fonction tapis" in Thom's and "distance function" in Mather's terminology), and the fibrations and tubular functions associated to the strata are compatible with each other. Thom–Mather stratifications satisfy the Thom first and second isotopy lemmas (see below), providing results such as local topological triviality of the stratification, local topological triviality along the strata of a morphism and topological stability of generic smooth mappings ( "generic" meaning transverse to the natural stratification of the jet space).
The word "stratification" has been introduced by R. Thom in [a5]. He proposed regularity conditions on how the strata of a stratification should fit together and stated the isotopy lemmas. The notes [a4] of J. Mather provide a detailed proof, with improvements and simplifications (cf. [a2], which contains an excellent history of stratification theory).
A Thom–Mather stratification of a space $M$ consists of a tube system $( T _ { X } , \pi _ { X } , \rho _ { X } )$ associated to the strata $X$ of $M$, such that $T _ { X }$ is a tubular neighbourhood of $X$ in $M$, $\pi _ { X } : T _ { X } \rightarrow X$ is the fibre projection associated to $T _ { X }$ and the tubular function $\rho _ { X } : T _ { X } \rightarrow \mathbf{R}$ is a continuous mapping satisfying $\rho _ { X } ^ { - 1 } ( 0 ) = X$. These data are controlled in the following sense: If $X$ and $Y$ are two strata such that $X$ is in the frontier of $Y$, then
i) the restriction mapping $( \pi _ { X } , \rho _ { X } ) : T _ { X } \cap Y \rightarrow X \times ]0 , \infty [$ is a smooth submersion;
ii) for $a \in T _ { X } \cap T _ { Y }$ such that $\pi_Y ( a ) \in T _ { X }$, there are commutation relations
C1) $\pi _X \circ \pi_ Y ( a ) = \pi_ X ( a )$,
C2) $\rho _ { X } \circ \pi _ { Y } ( a ) = \rho _ { X } ( a )$ whenever both sides of the formulas are defined.
Thom–Mather stratifications satisfy the isotopy lemmas (as proposed by Thom):
1) For every surjective stratified morphism $f : M \rightarrow N$, the restriction of $f$ to the inverse image $f ^ { - 1 } ( S )$ of a stratum $S$ is a fibration.
2) If there is a sequence of stratified morphisms $M \stackrel { f } { \rightarrow } N \stackrel { \pi } { \rightarrow } I$, where $f$ is a Thom mapping (an "application sans éclatement" ) and $I$ is a segment, then the mappings $f _ { a }$ and $f _ { b }$ over two points $a$ and $b$ in $I$ have the same topological type, i.e. there are homeomorphisms $h$ and $h ^ {\prime }$ such that the following diagram commutes:
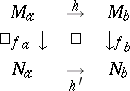 |
The importance of Thom–Mather stratifications is emphasized by their applications to stability and topological triviality theorems. Among other important results in singularity theory is the fact that any Whitney stratification (see Stratification) is a Thom–Mather stratification. Hence, a Whitney stratification satisfies topological triviality. The converse is false [a1]; in fact, being a Whitney stratification is equivalent to topological triviality for all sections by a generic flag [a3].
References
| [a1] | J. Briançon, J.P. Speder, "La trivialité topologique n'implique pas les conditions de Whitney" Note C.R. Acad. Sci. Paris Ser. A , 280 (1975) pp. 365 |
| [a2] | M. Goresky, R. MacPherson, "Stratified Morse theory" , Springer (1988) |
| [a3] | D.T. Lê, B. Teissier, "Cycles évanescents, sections planes et conditions de Whitney II" , Proc. Symp. Pure Math. , 40 , Amer. Math. Soc. (1983) pp. 65–103 |
| [a4] | J. Mather, "Notes on topological stability" , Harvard Univ. (1970) (Mimeographed notes) |
| [a5] | R. Thom, "La stabilité topologique des applications polynomiales" Enseign. Math. , 8 : 2 (1962) pp. 24–33 |
| [a6] | R. Thom, "Ensembles et morphismes stratifiés" Bull. Amer. Math. Soc. , 75 (1969) pp. 240–284 |
| [a7] | H. Whitney, "Local properties of analytic varieties" S. Cairns (ed.) , Differential and Combinatorial Topology , Princeton Univ. Press (1965) pp. 205–244 |
| [a8] | H. Whitney, "Tangents to an analytic variety" Ann. of Math. , 81 (1965) pp. 496–549 |
Thom-Mather stratification. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Thom-Mather_stratification&oldid=50687