Symmetric group
The group of all permutations (self-bijections) of a set $ X $
with the operation of composition (see Permutation group). The symmetric group on a set $ X $
is denoted by $ S ( X) $.
For equipotent $ X $
and $ X ^ \prime $
the groups $ S ( X) $
and $ S ( X ^ \prime ) $
are isomorphic. The symmetric group of a finite set $ X = \{ 1 \dots n \} $
is denoted by $ S _ {n} $.
Every abstract group is isomorphic to a subgroup of the symmetric group $ S ( X) $
of some set $ X $(
Cayley's theorem).
Let $ X $ be a finite set. Every permutation $ \pi $ on $ X $ can be uniquely described as a product of disjoint cycles (the (disjoint) cycle decomposition of a permutation); the sequence of integers
$$ z ( \pi ) = ( a _ {1} \dots a _ {n} ), $$
where $ a _ {i} $ is the number of cycles of length $ i $ of $ \pi $, is called the cycle type (or cycle index) of $ \pi $. Two permutations $ \pi $ and $ \pi ^ \prime $ are conjugate in $ S _ {n} $ if and only if they have the same cycle type. Permutations with cycle type
$$ \{ n - 2, 1, 0 \dots 0 \} $$
are called transpositions; they form a system of generators for $ S _ {n} $. The set of transpositions $ \Sigma = \{ ( i, i + 1) : i = 1 \dots n - 1 \} $ is a minimal set of generators for $ S _ {n} $. In general, a set $ \Delta = \{ ( i _ {k} , j _ {k} ) : i _ {k} \neq j _ {k} \} $ generates $ S _ {n} $ if the graph with $ X $ as set of vertices and the pairs $ ( i _ {k} , j _ {k} ) $ as edges is a tree [2]. The number of such generating sets is $ n ^ {n - 2 } $.
The alternating group $ A _ {n} $ is a normal subgroup of $ S _ {n} $. If $ n \neq 4 $, $ A _ {n} $ is the unique non-trivial proper normal subgroup, and $ S _ {4} $ contains only one other non-trivial normal subgroup — the Klein four-group: $ K _ {4} = \{ 1, ( 1 2)( 3, 4), ( 1 3)( 2 4), ( 1 4) ( 2 3) \} $. For $ n \leq 4 $ the group $ S _ {n} $ is solvable, but for $ n \geq 5 $ it is not solvable and $ A _ {n} $ is a simple non-Abelian group. Hölder's theorem: For $ n \neq 2, 6 $, the group $ S _ {n} $ is complete (see Complete group). The group $ S _ {2} $ is commutative, and $ S _ {6} $ has an outer automorphism of order 2.
All maximal intransitive and imprimitive subgroups in $ S _ {n} $ are known. For each partition $ n = m _ {1} + m _ {2} $, $ m _ {1} \neq m _ {2} $, the only maximal intransitive subgroups in $ S _ {n} $ are the subgroups $ S _ {m _ {1} } \times S _ {m _ {2} } $. The only transitive imprimitive maximal subgroups in $ S _ {n} $ are the wreath products (cf. Wreath product) of $ S _ {m _ {1} } $ with $ S _ {m _ {2} } $( for every decomposition $ n = m _ {1} m _ {2} $). The primitive maximal subgroups in $ S _ {n} $ have not yet been described (1992), but certain infinite series of them are known. For example, $ S _ {n} $ acts naturally on the set $ B _ {n} ^ {m} $ of all subsets of $ m $ elements of $ \{ 1 \dots n \} $; for $ n \neq 2m $ this determines a primitive group of permutations of $ B _ {n} ^ {m} $. It is maximal in $ S ( B _ {n} ^ {m} ) $ if $ ( m, n) \neq ( 2, 6) $, $ ( 2, 8) $, $ ( 3, 10) $, $ ( 4, 12) $, $ ( m, 2m) $, $ ( m, 2m + 1) $( see [1]). Another series is obtained by considering the group $ \Gamma L _ {n} ( q) $ of semi-linear transformations of the $ n $- dimensional vector space over the finite field of $ q $ elements. This group defines a primitive group of permutations of the Grassmann manifold $ G _ {n,m} ( q) $, $ 1 \leq m \leq n - 1 $, which is maximal in $ S ( G _ {n,m} ( q)) $ for $ n \geq 3 $.
Let $ X $ be an infinite set. The group of all permutations of $ X $ that move only a finite number of elements of $ X $ is called the finitary, or restricted, symmetric group on $ X $, and is denoted by $ \mathop{\rm SF} ( X) $; its subgroup of even permutations is called the finite, or restricted, alternating group on $ X $, and is denoted by $ \mathop{\rm AF} ( X) $. The subgroups $ \mathop{\rm SF} ( X) $ and $ \mathop{\rm AF} ( X) $ are normal in $ S ( X) $. More generally, let $ \alpha $ be the cardinality of $ X $ and let $ \beta \leq \alpha $ be an infinite cardinal; the set of permutations of $ X $ which move at most $ \beta $ elements of $ X $ is a subgroup of $ S ( X) $, denoted by $ S _ \beta ( X) $. Along with $ \mathop{\rm SF} ( X) $ and $ \mathop{\rm AF} ( X) $, the groups $ S _ \beta ( X) $ are normal subgroups in $ S ( X) $ for all $ \beta \leq \alpha $, and in fact there are no other non-trivial normal subgroups in $ S ( X) $( the Schreier–Ulam–Baer theorem, see [3]).
See also the references to Permutation of a set.
References
| [1] | L.A. Kaluzhnin, M.Kh. Klin, "On certain maximal subgroups of symmetric and alternating groups" Math. USSR Sb. , 16 : 1 (1972) pp. 95–123 Mat. Sb. , 87 : 1 (1972) pp. 91–121 |
| [2] | O. Ore, "Theory of graphs" , Amer. Math. Soc. (1962) |
| [3] | B.I. Plotkin, "Groups of automorphisms of algebraic systems" , Wolters-Noordhoff (1972) |
| [4] | V.A. Ustimenko-Bakumovskii, "Maximality of the group 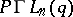 acting on subspaces of dimension acting on subspaces of dimension 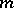 " Soviet Math. Dokl. , 19 : 3 (1978) pp. 769–772 Dokl. Akad. Nauk SSSR , 240 : 6 (1978) pp. 1305–1308 " Soviet Math. Dokl. , 19 : 3 (1978) pp. 769–772 Dokl. Akad. Nauk SSSR , 240 : 6 (1978) pp. 1305–1308 |
Comments
See also [a1] for a result on the structure of subgroups of $ S _ {n} $.
References
| [a1] | I.M. Aschbacher, L.L. Scott, "Maximal subgroups of finite groups" J. Algebra (1985) pp. 44–80 |
| [a2] | H. Wielandt, "Finite permutation groups" , Acad. Press (1964) (Translated from German) |
| [a3] | D. Passman, "Permutation groups" , Benjamin (1968) |
Symmetric group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Symmetric_group&oldid=48927