Summation methods
summability methods
Methods for constructing generalized sums of series, generalized limits of sequences, and values of improper integrals.
In mathematical analysis, the need arises to generalize the concept of the sum of a series (limit of a sequence, value of an integral) to include the case where the series (sequence, integral) diverges in the ordinary sense. This generalization usually takes the form of a rule or operation, and is called a summation method.
1) The Fourier series of a continuous 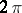 -periodic function
-periodic function 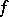 can be divergent on an infinite set of points
can be divergent on an infinite set of points 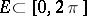 . The sequence
. The sequence 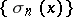 of arithmetical averages of the first
of arithmetical averages of the first  partial sums of this series,
partial sums of this series,
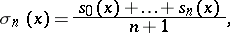 | (1) |
converges uniformly on the whole  -axis to
-axis to  . If the sum of the series is defined as
. If the sum of the series is defined as
 |
then in this sense the Fourier series of  will converge uniformly to
will converge uniformly to  on the whole
on the whole  -axis.
-axis.
2) A series
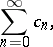 | (2) |
obtained as a result of multiplying two series
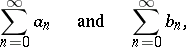 |
which converge respectively to 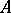 and
and 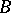 , may prove to be divergent. If the sum of the series (2) is defined as in example 1), i.e. as the limit of the sequence of arithmetical averages of the first
, may prove to be divergent. If the sum of the series (2) is defined as in example 1), i.e. as the limit of the sequence of arithmetical averages of the first  partial sums, then in this sense the product of the two given series will converge to the sum
partial sums, then in this sense the product of the two given series will converge to the sum 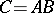 .
.
3) The power series
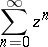 | (3) |
converges for 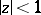 to the sum
to the sum  and diverges for
and diverges for 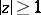 . If the sum of (3) is defined as
. If the sum of (3) is defined as
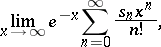 |
where 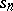 are the partial sums of (3), then in this sense (3) will converge for all
are the partial sums of (3), then in this sense (3) will converge for all  that satisfy the condition
that satisfy the condition 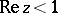 , and its sum will be the function
, and its sum will be the function 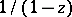 (see Borel summation method).
(see Borel summation method).
The most important properties of summation methods are regularity (see Regular summation methods) and linearity (see Linear summation method). The most common summation methods possess these properties. Many methods also possess the property of translativity (see Translativity of a summation method). Matrix summation methods and semi-continuous summation methods form a broad class of summation methods (cf. Matrix summation method; Semi-continuous summation method). These methods are linear, and regularity conditions have been constructed for them. Matrix summation methods include, in particular, the Voronoi summation method and the Cesàro summation methods. Methods defined by matrices with a finite number of rows (see Row-finite summation method) and particularly by triangular matrices (see Triangular summation method) form a subclass of the matrix summation methods. Among the semi-continuous summation methods are the Abel summation method, the Borel summation method, the Mittag-Leffler summation method, the Lindelöf summation method, and the Riesz summation method. Summation methods of other forms than the forms shown do exist, such as the Borel integral summation method and the Hölder summation methods.
The same sequence (series) may be summable by one method, but not by another. The set of all sequences (series) that are summable by a given method is called the summability field of the given method.
If one considers two summation methods, and the summability field of one method contains the summability field of the other, then one speaks of the inclusion of summation methods; when the fields coincide, one speaks of the equivalence of the summation methods. If the field of a summation method consists only of convergent sequences, then one says that the summation method is equivalent to convergence. Establishing conditions under which the inclusion of summation methods can occur is one of the problems of the theory of summability. Two or more summation methods may be compatible or non-compatible. Summation methods are said to be compatible if they cannot sum one and the same sequence to different limits. In those cases where from the summability of the series
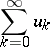 |
by a method 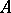 it follows that the series
it follows that the series
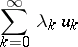 |
is summable by a method 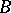 , one says that the numbers
, one says that the numbers 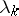 are summability multipliers of type
are summability multipliers of type 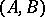 .
.
There are two distinct types of theorems on summation methods. In theorems of the first (Abelian) type, the properties of a sequence enable one to infer the properties of the averages of this sequence obtained as a result of the transformation defining the summation method. For example, Cauchy's theorem establishes that 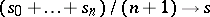 always follows from
always follows from 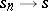 . In theorems of the second (Tauberian) type, the properties of the averages corresponding to the given summation method plus additional conditions enable one to infer the properties of the transformed sequence (see Tauberian theorems).
. In theorems of the second (Tauberian) type, the properties of the averages corresponding to the given summation method plus additional conditions enable one to infer the properties of the transformed sequence (see Tauberian theorems).
By analogy with ordinary convergence, concepts of special forms of summability are introduced: absolute summability, unconditional summability, strong summability, almost-summability, 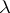 -summability, and others.
-summability, and others.
The concept of a generalized limit has also been applied to functions and integrals. In these cases one speaks of the summation of a function (or of an integral). For example, for a function 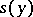 , defined for all
, defined for all 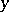 , a summation method analogous to the matrix summation method of sequences consists of the fact that an integral transform
, a summation method analogous to the matrix summation method of sequences consists of the fact that an integral transform
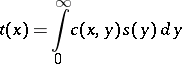 |
with a kernel 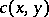 is examined, and the number
is examined, and the number  is associated to the function
is associated to the function 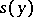 as its generalized limit, as
as its generalized limit, as 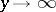 , if
, if
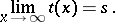 |
In the same way, one of the summation methods of improper integrals
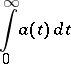 | (4) |
consists of the fact that transforms
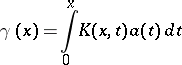 |
with a kernel 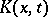 are examined, and the integral (4) is called summable to the value
are examined, and the integral (4) is called summable to the value  if
if
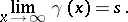 |
The definition of a summation method, introduced for the summation of sequences of numbers and functions, is generalized to include sequences of elements of any set, and a general definition of a summation method can be formulated thus: Let 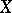 be a given set, let
be a given set, let 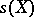 be a set of sequences
be a set of sequences 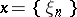 with elements
with elements 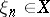 , and let
, and let 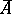 be an operator defined on a subset
be an operator defined on a subset 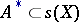 with values in
with values in 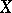 . The pair
. The pair 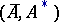 is then called a summation method defined on
is then called a summation method defined on 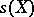 , and
, and 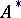 is called the summability field. In this case, a sequence
is called the summability field. In this case, a sequence 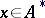 (or the series
(or the series 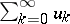 with terms
with terms 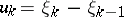 ) is said to be summable to the limit
) is said to be summable to the limit 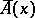 , where
, where 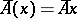 .
.
References
| [1] | G.H. Hardy, "Divergent series" , Clarendon Press (1949) |
| [2] | R.G. Cooke, "Infinite matrices and sequence spaces" , Macmillan (1950) |
| [3] | G.F. Kangro, "Theory of summability of sequences and series" J. Soviet Math. , 5 : 1 (1970) pp. 1–45 Itogi Nauk. i Tekhn. Mat. Anal. , 12 (1974) pp. 5–70 |
| [4] | S.A. Baron, "Introduction to the theory of summability of series" , Tartu (1966) (In Russian) |
| [5] | A. Peyerimhoff, "Lectures on summability" , Springer (1969) |
| [6] | K. Knopp, "Theorie und Anwendung der unendlichen Reihen" , Springer (1964) (English translation: Blackie, 1951 & Dover, reprint, 1990) |
| [7] | K. Zeller, W. Beekmann, "Theorie der Limitierungsverfahren" , Springer (1970) |
| [8] | H. Pitt, "Tauberian theorems" , Oxford Univ. Press (1958) |
| [9] | T.H. Ganelius, "Tauberian remainder theorems" , Springer (1971) |
| [10] | G.M. Petersen, "Regular matrix transformations" , McGraw-Hill (1966) |
| [11] | A.L. Brudno, "Summation of bounded sequences by matrices" Mat. Sb. , 16 (58) : 2 (1945) pp. 191–247 (In Russian) ((English abstract)) |
Comments
References
| [a1] | C.N. Moore, "Summable sequences and convergence factors" , Dover, reprint (1966) |
Summation methods. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Summation_methods&oldid=11209