Steinberg module
Let  , the group of all invertible
, the group of all invertible 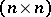 -matrices over the finite field
-matrices over the finite field  with
with  elements and characteristic
elements and characteristic  , let
, let  be the subgroup of all superdiagonal elements, let
be the subgroup of all superdiagonal elements, let  be the subgroup of elements of
be the subgroup of elements of  whose diagonal entries are all
whose diagonal entries are all  , and let
, and let 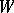 be the subgroup of permutation matrices. In the group algebra
be the subgroup of permutation matrices. In the group algebra  of
of 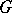 over any field
over any field 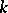 of characteristic
of characteristic  or
or 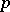 , the element
, the element
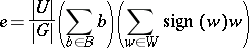 |
is an idempotent, called the Steinberg idempotent, and the 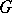 -module that it generates in
-module that it generates in 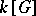 by right multiplication is called the Steinberg module (see [a8]) and is commonly denoted
by right multiplication is called the Steinberg module (see [a8]) and is commonly denoted 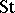 (as are all modules isomorphic to it). A similar construction holds for any finite group
(as are all modules isomorphic to it). A similar construction holds for any finite group  of Lie type (and for any
of Lie type (and for any  -pair, which is an axiomatic generalization due to J. Tits) defined over a field of characteristic
-pair, which is an axiomatic generalization due to J. Tits) defined over a field of characteristic 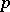 with
with 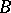 replaced by a Borel subgroup (which is a certain kind of solvable subgroup),
replaced by a Borel subgroup (which is a certain kind of solvable subgroup), 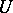 by a maximal unipotent subgroup (cf. Unipotent group) of
by a maximal unipotent subgroup (cf. Unipotent group) of 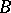 (which is also a Sylow
(which is also a Sylow 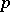 -subgroup of
-subgroup of 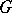 ; cf. also Sylow subgroup;
; cf. also Sylow subgroup; 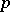 -group) and
-group) and 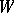 by the corresponding Weyl group.
by the corresponding Weyl group. 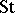 is always irreducible and it has
is always irreducible and it has 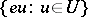 as a basis, so that its dimension is
as a basis, so that its dimension is 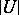 (see [a8]). Its character values are given as follows [a3]. If
(see [a8]). Its character values are given as follows [a3]. If  has order prime to
has order prime to 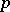 , then
, then 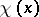 equals, up to a sign which can be determined, the order of a Sylow
equals, up to a sign which can be determined, the order of a Sylow 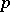 -subgroup of the centralizer of
-subgroup of the centralizer of  ; otherwise it equals
; otherwise it equals  .
.
In case the characteristic of 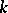 equals
equals  ,
, 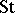 has the following further properties [a5]. It is the only module (for
has the following further properties [a5]. It is the only module (for  ) which is both irreducible and projective. As an irreducible module it is the largest (in dimension), and as a projective module it is the smallest since it is a tensor factor of every projective module. It follows that it is also self-dual and that every projective module is also injective and vice versa. Because of these remarkable properties,
) which is both irreducible and projective. As an irreducible module it is the largest (in dimension), and as a projective module it is the smallest since it is a tensor factor of every projective module. It follows that it is also self-dual and that every projective module is also injective and vice versa. Because of these remarkable properties, 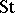 plays a prominent role in ongoing work in the still (2000) unresolved problem of determining all of the irreducible
plays a prominent role in ongoing work in the still (2000) unresolved problem of determining all of the irreducible 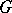 -modules (with characteristic
-modules (with characteristic  still equal to
still equal to  ), or equivalently, as it turns out, of determining all of the irreducible rational
), or equivalently, as it turns out, of determining all of the irreducible rational 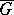 -modules, where
-modules, where 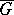 is the algebraic group obtained from
is the algebraic group obtained from 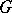 by replacing
by replacing 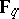 by its algebraic closure
by its algebraic closure 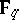 , i.e., where
, i.e., where 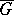 is any simple affine algebraic group of characteristic
is any simple affine algebraic group of characteristic 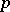 (see [a6]). This equivalence comes from the fact that every irreducible
(see [a6]). This equivalence comes from the fact that every irreducible 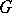 -module extends to a rational
-module extends to a rational  -module. In particular,
-module. In particular, 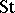 extends to the
extends to the 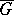 -module with highest weight
-module with highest weight 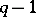 times the sum of the fundamental weights, which is accordingly also denoted
times the sum of the fundamental weights, which is accordingly also denoted  , or
, or 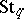 since there is one such
since there is one such 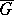 -module for each
-module for each 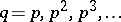 . These modules are ubiquitous in the module theory of
. These modules are ubiquitous in the module theory of 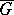 and figure prominently, for example, in the proofs of many cohomological vanishing theorems and in W. Haboush's proof of the Mumford hypothesis (see [a4]).
and figure prominently, for example, in the proofs of many cohomological vanishing theorems and in W. Haboush's proof of the Mumford hypothesis (see [a4]).
Back in the finite case, some other constructions of 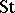 , with the characteristic of
, with the characteristic of 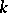 now equal to
now equal to  , are as follows. According to C.W. Curtis [a2]
, are as follows. According to C.W. Curtis [a2]
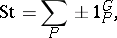 |
in which 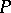 runs through the
runs through the 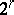 (
( equal to the rank of
equal to the rank of 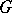 ) (parabolic) subgroups of
) (parabolic) subgroups of 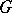 containing
containing  ,
, 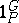 is the
is the 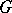 -module induced by the trivial
-module induced by the trivial 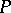 -module, and the
-module, and the 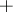 or
or  is used according as the rank
is used according as the rank 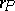 of
of 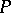 is even or odd. For
is even or odd. For 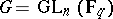 , for example, there is one
, for example, there is one  for each solution of
for each solution of 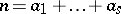 (
(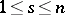 , each
, each 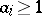 ); it consists of all of the elements of
); it consists of all of the elements of 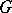 that are superdiagonal in the corresponding block matrix form. A third construction, due to L. Solomon and Tits [a7], yields
that are superdiagonal in the corresponding block matrix form. A third construction, due to L. Solomon and Tits [a7], yields 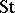 as the top homology space
as the top homology space 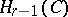 for the Tits simplicial complex or Tits building
for the Tits simplicial complex or Tits building 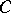 of
of 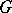 , formed as follows: corresponding to each parabolic subgroup
, formed as follows: corresponding to each parabolic subgroup 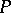 there exists an
there exists an 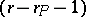 -simplex
-simplex 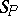 in
in 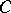 , and
, and  is a facet of
is a facet of 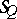 just when
just when 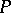 contains
contains  . These three constructions are, in fact, closely related to each other (see [a9]). In particular, the idempotent
. These three constructions are, in fact, closely related to each other (see [a9]). In particular, the idempotent  used at the start can be identified with an
used at the start can be identified with an 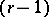 -sphere in the Tits building, the sum over
-sphere in the Tits building, the sum over 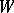 corresponding to a decomposition of the sphere into simplexes: in the usual action of
corresponding to a decomposition of the sphere into simplexes: in the usual action of 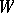 on
on 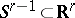 the reflecting hyperplanes divide
the reflecting hyperplanes divide 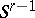 into
into 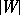 oriented spherical simplexes, each of which is a fundamental domain for
oriented spherical simplexes, each of which is a fundamental domain for 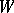 . Finally,
. Finally, 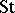 has a simple presentation (as a linear space). It is generated by the Borel subgroups of
has a simple presentation (as a linear space). It is generated by the Borel subgroups of 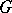 subject only to the relations that for every parabolic subgroup of rank
subject only to the relations that for every parabolic subgroup of rank 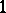 the sum of the Borel subgroups that it contains is
the sum of the Borel subgroups that it contains is  .
.
There are also infinite-dimensional versions of the above constructions, usually for reductive Lie groups — real, complex or 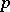 -adic — such as
-adic — such as 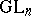 . The
. The 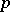 -adic case most closely resembles the finite case. There, the affine Weyl group and a certain compact-open subgroup, called an Iwahori subgroup, come into play (in place of
-adic case most closely resembles the finite case. There, the affine Weyl group and a certain compact-open subgroup, called an Iwahori subgroup, come into play (in place of 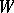 and
and 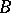 ), and the three constructions agree. In [a1] several types of buildings, Curtis' formula and the Steinberg idempotent, in the guise of a homology cycle, all appear. In the infinite case the constructed object is sometimes called the Steinberg representation, sometimes the special representation.
), and the three constructions agree. In [a1] several types of buildings, Curtis' formula and the Steinberg idempotent, in the guise of a homology cycle, all appear. In the infinite case the constructed object is sometimes called the Steinberg representation, sometimes the special representation.
References [a5] and [a9] are essays on 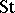 .
.
References
| [a1] | A. Borel, J-P. Serre, "Cohomologie d'immeubles et de groupes 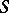 -arithmétiques" Topology , 15 (1976) pp. 211–232 -arithmétiques" Topology , 15 (1976) pp. 211–232 |
| [a2] | C.W. Curtis, "The Steinberg character of a finite group with 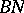 -pair" J. Algebra , 4 (1966) pp. 433–441 -pair" J. Algebra , 4 (1966) pp. 433–441 |
| [a3] | C.W. Curtis, G.I. Lehrer, J. Tits, "Spherical buildings and the character of the Steinberg representation" Invent. Math. , 58 (1980) pp. 201–220 |
| [a4] | W. Haboush, "Reductive groups are geometrically reductive" Ann. of Math. , 102 (1975) pp. 67–83 |
| [a5] | J.E. Humphreys, "The Steinberg representation" Bull. Amer. Math. Soc. (N.S.) , 16 (1987) pp. 237–263 |
| [a6] | J.C. Jantzen, "Representations of algebraic groups" , Acad. Press (1987) |
| [a7] | L. Solomon, "The Steinberg character of a finite group with 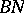 -pair" , Theory of Finite Groups (Harvard Symp.) , Benjamin (1969) pp. 213–221 -pair" , Theory of Finite Groups (Harvard Symp.) , Benjamin (1969) pp. 213–221 |
| [a8] | R. Steinberg, "Prime power representations of finite linear groups II" Canad. J. Math. , 9 (1957) pp. 347–351 |
| [a9] | R. Steinberg, "Collected Papers" , Amer. Math. Soc. (1997) pp. 580–586 |
Steinberg module. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Steinberg_module&oldid=18782