Steenrod reduced power
A stable cohomology operation 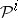 ,
, 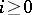 , of the type
, of the type 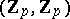 , where
, where 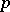 is a fixed odd prime number, which is the analogue modulo
is a fixed odd prime number, which is the analogue modulo 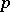 of the Steenrod square, and which is a homomorphism
of the Steenrod square, and which is a homomorphism
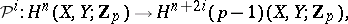 |
defined for every pair of topological spaces 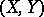 and any integer
and any integer  . The Steenrod reduced powers possess the following properties (apart from naturality
. The Steenrod reduced powers possess the following properties (apart from naturality 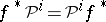 and stability
and stability 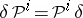 , where
, where 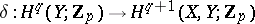 is the coboundary homomorphism):
is the coboundary homomorphism):
1) 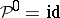 ;
;
2) if 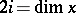 , then
, then 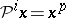 ;
;
3) if 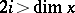 , then
, then 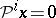 ;
;
4) (Cartan's formula) 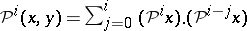 ;
;
5) (Adem's relation)
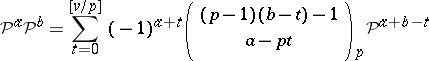 |
if 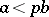 ,
,
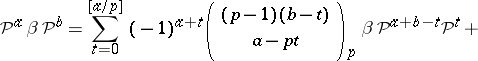 |
 |
if 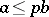 , where
, where 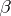 is the Bockstein homomorphism associated with the short exact sequence of coefficient groups
is the Bockstein homomorphism associated with the short exact sequence of coefficient groups 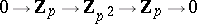 , while
, while 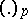 are the binomial coefficients reduced modulo
are the binomial coefficients reduced modulo 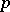 .
.
These properties are analogous to the corresponding properties of Steenrod squares, whereby the operation 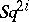 corresponds to the operation
corresponds to the operation 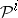 . Just as for Steenrod squares, the multiplication in 4) can be considered to be both exterior (
. Just as for Steenrod squares, the multiplication in 4) can be considered to be both exterior ( -multiplication) and interior (
-multiplication) and interior ( -multiplication). Steenrod reduced powers commute with suspension and transgression.
-multiplication). Steenrod reduced powers commute with suspension and transgression.
The properties 1)–3) uniquely characterize 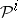 , and can be constructed in the same way as Steenrod squares using the minimal acyclic free chain
, and can be constructed in the same way as Steenrod squares using the minimal acyclic free chain 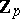 -complex
-complex 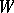 .
.
References
| [1] | N.E. Steenrod, D.B.A. Epstein, "Cohomology operations" , Princeton Univ. Press (1962) |
| [2] | Matematika , 5 : 2 (1961) pp. 3–11; 11–30; 30–49; 50–102 |
Comments
For more references see Steenrod algebra.
Steenrod reduced power. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Steenrod_reduced_power&oldid=15254