Steenrod operation

The general name for the stable cohomology operations (cf. Cohomology operation) created by N.E. Steenrod for every prime number 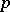. The first example is contained in [1]. For 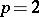this is the Steenrod square 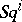, for 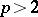the Steenrod reduced power 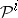. The operations 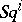multiplicatively generate the Steenrod algebra modulo 2, while the operations 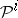together with the Bockstein homomorphism generate the Steenrod algebra modulo .

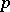References

[1]	N.E. Steenrod, "Products of cocycles and extensions of mappings" Ann. of Math. , 48 (1947) pp. 290–320
[2]	N.E. Steenrod, D.B.A. Epstein, "Cohomology operations" , Princeton Univ. Press (1962)
[3]	M.K. Tangora, "Cohomology operations and applications in homotopy theory" , Harper & Row (1968)

References

[a1]	R.M. Switzer, "Algebraic topology - homotopy and homology" , Springer (1975) pp. Chapt. 18
[a2]	J.F. Adams, "Stable homotopy and generalized homology" , Univ. Chicago Press (1974) pp. Part III, Chapt. 12