Steenrod algebra
The graded algebra  over the field
over the field  of all stable cohomology operations (cf. Cohomology operation) modulo
of all stable cohomology operations (cf. Cohomology operation) modulo  . For any space (spectrum of spaces)
. For any space (spectrum of spaces)  , the group
, the group  is a module over the Steenrod algebra
is a module over the Steenrod algebra  .
.
The Steenrod algebra is multiplicatively generated by the Steenrod operations (cf. Steenrod operation). Thus, the Steenrod algebra  is a graded associative algebra, multiplicatively generated by the symbols
is a graded associative algebra, multiplicatively generated by the symbols  with
with  , which satisfy the Adem relation:
, which satisfy the Adem relation:
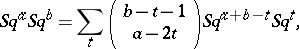 |
 , so that an additive basis (over
, so that an additive basis (over 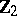 ) of the Steenrod algebra
) of the Steenrod algebra  consists of the operations
consists of the operations  ,
,  (the so-called Cartan–Serre basis). Similar results are true for
(the so-called Cartan–Serre basis). Similar results are true for 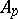 with
with  . Furthermore,
. Furthermore,
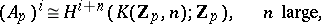 |
where 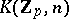 is an Eilenberg–MacLane space. The multiplication
is an Eilenberg–MacLane space. The multiplication
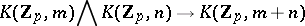 |
induces the diagonal  in
in  , which is a homomorphism of algebras, and, consequently, turns
, which is a homomorphism of algebras, and, consequently, turns  into a Hopf algebra.
into a Hopf algebra.
References
| [1] | N.E. Steenrod, D.B.A. Epstein, "Cohomology operations" , Princeton Univ. Press (1962) |
| [2] | J. Milnor, "The Steenrod algebra and its dual" Ann. of Math. , 67 (1958) pp. 150–171 |
| [3] | M.K. Tangora, "Cohomology operations and applications in homotopy theory" , Harper & Row (1968) |
Comments
The analogue of the Steenrod algebra for a cohomology theory defined by a spectrum  is
is 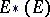 ; cf. Generalized cohomology theories and Spectrum of spaces. The
; cf. Generalized cohomology theories and Spectrum of spaces. The 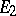 -term of the Adams spectral sequence, cf. Spectral sequence,
-term of the Adams spectral sequence, cf. Spectral sequence,  is a purely (homological) algebra construct obtained by regarding the homology groups as modules over the Hopf algebra
is a purely (homological) algebra construct obtained by regarding the homology groups as modules over the Hopf algebra  .
.
References
| [a1] | J. Dieudonné, "A history of algebraic and differential topology 1900–1960" , Birkhäuser (1989) |
| [a2] | R.M. Switzer, "Algebraic topology - homotopy and homology" , Springer (1975) pp. Chapts. 18–19 |
| [a3] | J.F. Adams, "Stable homotopy and generalized homology" , Univ. Chicago Press (1974) pp. Part III, Chapts. 12, 15 |
Steenrod algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Steenrod_algebra&oldid=12348