Statistical mechanics, mathematical problems in
2020 Mathematics Subject Classification: Primary: 82-01 [MSN][ZBL]
The totality of problems of mathematical physics that arise from trying to interpret accurately the basic concepts and facts of statistical mechanics. These problems can be conditionally divided into the following groups:
1) the foundations of the basic principles of statistical mechanics;
2) equilibrium ensembles at the thermodynamic limit, inference of thermodynamic relations;
3) phase transitions;
4) the evolution of ensembles, the relaxation problem, studies on kinetic and hydrodynamic equations;
5) basic states, elementary excitations (in the case of a quantum system).
In statistical mechanics, systems consisting of a large number of (microscopic) particles contained in a large (relative to the dimensions of the particles) domain $ V $ of the space $ \mathbf R ^ {3} $ are studied. Statistical mechanics, depending on the method used to describe the system, is divided into classical and quantum mechanics.
The description of the classical system contained in $ V $ involves giving the space $ X $ of possible states of each separate particle (single-particle space), as well as the totality $ \Omega _ {V} = \cup _ {N\geq } 0 X ^ {N} $ of admissible configurations $ \omega = \{ x _ {1}, \dots, x _ {N} \} $ ($ x _ {i} \in X $, $ i = 1, \dots, N $, $ N = 1, 2 , \dots $) of a finite number of particles within $ V $, and defining the energy $ H = H _ {V} ( \omega ) $ for every configuration $ \omega \in \Omega _ {V} $ and the law of the evolution of the system in time (also called the dynamics), i.e. the semi-group (more often an entire group) of transformations $ U _ {t} ^ {V} $, $ t \geq 0 $, of $ \Omega _ {V} $ onto itself which preserve the energy $ H _ {V} $:
$$ H _ {V} ( U _ {t} ^ {V} \omega ) = H _ {V} ( \omega ) $$
for any $ \omega \in \Omega _ {V} $ and any $ t $. In many cases, $ \Omega _ {V} $ naturally has a symplectic structure, and the transformations $ U _ {t} ^ {V} $ are produced by using solutions of the so-called Hamiltonian system of equations of motion, generated by the Hamilton function $ H = H _ {V} $ (see [1]). Moreover, a natural measure $ dx $ usually exists in the space $ X $ such that the measure $ d ^ {V} x = \oplus _ {N} d ^ {N} x $ in $ \Omega _ {V} $ ($ d ^ {N} x= dx \times \dots \times dx $ is the product measure on $ X ^ {N} $) is invariant relative to the evolutions $ U _ {t} ^ {V} $. However, for macroscopic systems consisting of a large number of particles, such a detailed description of their states and of the dynamics of these states (i.e. a description of the trajectories of each individual particle) proves to be almost impossible, and of no use anyway from the point of view of studying the macroscopic properties of the whole system. These properties are determined only by certain mean characteristics of the configuration $ \omega $, and of its evolution $ \omega ( t) $, $ t > 0 $, in time: for example, the fractions $ \rho _ {1} ( S; t) $, $ S \subset X $, of particles in $ \omega ( t) $ whose states belong to a given set $ S $ of a single-particle space $ X $, or the fractions $ \rho _ {2} ( S _ {1} , S _ {2} ; t _ {1} , t _ {2} ) $ of particles whose states at the moment of time $ t _ {1} $ belong to the set $ S _ {1} \subset X $, and at the moment of time $ t _ {2} $ belong to the set $ S _ {2} \subset X $, etc.
These concepts have given rise to the following radical idea: The state of a macroscopic system must be defined by a probability distribution $ {\mathsf P} $ on the phase space $ \Omega _ {V} $, whereby the evolution $ {\mathsf P} _ {t} $, $ t > 0 $, of this distribution in time is generated by the initial development of the system itself:
$$ \tag{1 } {\mathsf P} _ {t} ( A) = \ {\mathsf P} \{ ( U _ {t} ^ {V} ) ^ {-} 1 A \} ,\ \ A \subset \Omega _ {V} ; $$
here $ ( U _ {t} ^ {V} ) ^ {-} 1 A $ is the complete inverse image of the set $ A \subset \Omega _ {V} $ under the mapping $ U _ {t} ^ {V} $. This stipulation is complemented by the following postulate: For every "good" probability distribution $ {\mathsf P} $ on the phase space $ \Omega _ {V} $ and an appropriate physical quantity $ f $ (i.e. a real-valued function on $ \Omega _ {V} $), the values this quantity takes are, with probability close to one (calculated with respect to $ {\mathsf P} $), close to its mean value $ \langle f\rangle _ {\mathsf P} $. One of the problems related to statistical mechanics is to put this assertion into an exact form. One of the possible results is of the following kind: Let the distribution $ {\mathsf P} $ on $ \Omega _ {V} $ possess the property of rapidly-decreasing dependence (i.e. the probability distributions it generates of configurations for two subsystems, situated far apart, are almost independent), while the physical quantity is summable, i.e.
$$ \tag{2 } f( \omega ) = \ \sum \phi ( \omega \mid _ {S} ),\ S \subset [ 1, \dots, N],\ | S | = n, $$
where $ n \leq \infty $ is arbitrary, $ \phi ( x _ {1}, \dots, x _ {n} ) $ is a certain symmetric "local" function on $ X ^ {n} $ (i.e. $ \phi $ tends rapidly to zero as the points $ x _ {1}, \dots, x _ {n} $ move further away from each other), and $ \omega \mid _ {S} = \{ {x _ {i} } : {i \in S } \} $ if $ \omega = \{ {x _ {i} } : {i = 1, \dots, N } \} $. In this case $ \langle f\rangle _ {\mathsf P} \sim | V | $, and the fluctuation $ \Delta f = f - \langle f\rangle _ {\mathsf P} \sim | V | ^ {1/2} $ (with probability close to one for large $ | V | $), while the distribution of $ \Delta f/ | V | ^ {1/2} $ is close to normal (as before, when $ | V | \rightarrow \infty $, see [2]).
A probability distribution $ {\mathsf P} $ on a phase space is said to be an equilibrium distribution if it is invariant relative to the dynamics $ U _ {t} ^ {V} $. Apart from the energy $ H _ {V} = H _ {V} ^ {0} $, let there be several more so-called integrals of motion $ H _ {V} ^ {1}, \dots, H _ {V} ^ {k} $, i.e. functions on $ \Omega _ {V} $ that are invariant relative to $ U _ {t} ^ {V} $ (for example, the number of particles in the system, the total momentum of the particles, the total spin, etc.). Every distribution on $ \Omega _ {V} $ of the form
$$ d {\mathsf P} = f( H _ {V} ^ {0}, \dots, H _ {V} ^ {k} ) d ^ {V} x, $$
where $ d ^ {V} x $ is the invariant measure on $ \Omega _ {V} $ and $ f > 0 $ is a function (possibly generalized), is an equilibrium distribution. An equilibrium distribution defined by a density of the form
$$ \tag{3 } f( \xi ^ {0},\dots, \xi ^ {k} ) = \ Q ^ {-1} \prod _ { i= 0} ^ { k } \delta ( \xi ^ {i} - \overline \xi ^ {i} ),\ \ \overline \xi ^ {i} \in \mathbf R ,\ \ i = 0, \dots, k $$
( $ Q ^ {-1} $ is a normalizing factor), is called a microcanonical distribution (or microcanonical ensemble), concentrated on the surface
$$ \tag{4 } S _ {\overline \xi ^ {0}, \dots, \overline \xi ^ {k} } = \ \{ {\omega \in \Omega _ {V} } : {H ^ {i} ( \omega ) = \overline \xi \; {} ^ {i} , i = 0, \dots k } \} $$
of constancy of first integrals.
In statistical mechanics it is postulated that the microcanonical distribution (3) is an equilibrium distribution (i.e. the mean values of the physical variables calculated by means of (3) coincide with great accuracy with the experimentally-measured values). For a long time it was believed that in order to prove this postulate, an unknown ergodic hypothesis had to be demonstrated: If $ H _ {V} ^ {0}, \dots, H _ {V} ^ {k} $ is a complete set of (smooth) integrals of motion, the microcanonical distribution is the unique (smooth) equilibrium distribution of any surface $ S _ {\overline \xi ^ {0}, \dots, \overline \xi ^ {k} } $. Attempts to prove this hypothesis gave rise to modern ergodic theory (see [3], [4]). Now, however, it has become clear that the ergodicity of finite systems is an unnecessarily-strict assumption: In order to prove the postulate on microcanonical distributions it is sufficient to establish the ergodicity of the system at the thermodynamic limit $ V \uparrow \mathbf R ^ {3} $. Apart from the microcanonical distribution, the Gibbs equilibrium distribution (sometimes called a grand canonical ensemble) is often studied. It is defined by the density
$$ \tag{5 } f = Z ^ {-1} \mathop{\rm exp} \{ - \beta ( H _ {V} ^ {0} + \mu _ {1} H _ {V} ^ {1} + \dots + \mu _ {k} H _ {V} ^ {k} ) \} , $$
where $ Z ^ {-1} $ is a normalizing factor, $ \beta > 0 $ and $ \mu _ {1} \dots \mu _ {k} $ are arbitrary real parameters (the parameter $ \beta = 1/kT $, where $ T $ is the absolute temperature and $ k $ is an absolute constant, the so-called Boltzmann constant). Intermediate distributions are also sometimes studied (small canonical ensembles); these have a density of the form
$$ \tag{6 } f = \widetilde{Z} ^ {-1} \mathop{\rm exp} \{ - \beta ( H _ {V} ^ {0} + \mu _ {i _ {1} } H _ {V} ^ {i _ {1} } + \dots + \mu _ {i _ {s} } H _ {V} ^ {i _ {s} } ) \} \times $$
$$ \times \prod _ { p= 1} ^ { k- s} \delta ( H _ {j _ {p} } - \overline \xi _ {j _ {p} } ), $$
where $ i _ {1}, \dots, i _ {s} $ and $ j _ {1}, \dots, j _ {p} $ are two complementary subsets of indices in $ ( 1, \dots, k) $. The Gibbs distribution (5), as well as a distribution (6), is in many ways more convenient than the microcanonical distribution (3), and the use of both is justified by the following hypothesis — the so-called equivalence principle of ensembles: For "suitable" physical quantities on $ \Omega _ {V} $ (for example, for a summable quantity of the form (2)), given values of the parameters $ \beta , \mu _ {1}, \dots, \mu _ {k} $ for which only one equilibrium phase exists, the mean $ \langle f\rangle _ {\beta , \mu _ {1}, \dots, \mu _ {k} } $, calculated using the Gibbs distribution (5) for large $ V $, is close to the mean $ \langle f\rangle _ {\overline \xi ^ {0}, \dots, \overline \xi ^ {k} } $, calculated using a microcanonical ensemble on the surface $ S _ {\overline \xi ^ {0} , \dots, \overline \xi ^ {k} } $, where $ \langle \overline \xi ^ {i} \rangle = \langle H _ {V} ^ {i} \rangle _ {\beta , \mu _ {1}, \dots, \mu _ {k} } $. The proof of this equivalence also constitutes one of the general mathematical problems of statistical mechanics and thermodynamics (see [5], [6], [7]).
The accepted method of describing systems in statistical mechanics is justified when the domain $ V $ has sufficiently-large volume, in other words, statistical mechanics studies the asymptotic properties of systems in the limit $ V \uparrow \mathbf R ^ {3} $ (i.e. a sequence of systems of one and the same particles, contained respectively in the volumes $ V _ {1} \subset V _ {2} \subset \cdots $, where $ \cup _ {n} V _ {n} = \mathbf R ^ {3} $). This passage to the limit is usually called a thermodynamic passage to the limit. One of the primary problems related to the thermodynamic limit is, beginning with equilibrium ensembles, to define the so-called thermodynamic potentials and relations. It proves possible to find all thermodynamic potentials, when $ V \uparrow \mathbf R ^ {3} $, from the asymptotics of the normalizing factors $ Q ^ {-1} $, $ Z ^ {-1} $, $ \widetilde{Z} ^ {-1} $, etc., in the ensembles (3), (5), (6); for example, the Gibbs thermodynamic potential is equal to
$$ \tag{7 } p( \beta , \mu _ {1}, \dots, \mu _ {k} ) = \lim\limits _ {V \uparrow \mathbf R ^ {3} } \frac{ \mathop{\rm ln} \ Z }{| V | } , $$
where $ Z ^ {-1} $ is the normalizing factor in the Gibbs ensemble (5). Other thermodynamic functions are introduced in the same way, and relations linking them are established. The majority of mathematical problems which arise here (existence of a limit, properties of thermodynamic potentials, etc.) have been studied fairly comprehensively, although a number of unsolved problems do remain (see, for example, [7]).
Since the end of the 1960's, the following general approach has found favour in mathematical statistical mechanics: instead of studying the asymptotic properties of finite systems in a thermodynamic passage to the limit, one should consider idealized infinite systems constructed in a particular way, whose characteristics coincide with the asymptotics being studied (this point of view was encountered in earlier works in less obvious form). Examining infinite systems gives a visible meaning to the somewhat formal procedure of a thermodynamic passage to the limit, and makes it possible to do without it altogether. The phase space $ \Omega _ \infty $ of an infinite system consists of infinite configurations of particles $ \omega = \{ x _ {1} , x _ {2} ,\dots \} $, $ x _ {i} \in X ^ {V} $, $ i = 1, 2, \dots $ located throughout $ \mathbf R ^ {3} $, while their dynamics $ U _ {t} ^ \infty : \Omega _ \infty \rightarrow \Omega _ \infty $, $ t \in \mathbf R $, is constructed as the limit of the dynamics $ U _ {t} ^ {V} $ of finite systems as $ V \uparrow \mathbf R ^ {3} $. The macroscopic states of an infinite system are defined by probability distributions on the space $ \Omega _ \infty $, which develop in line with the dynamics $ U _ {t} ^ \infty $ in $ \Omega _ \infty $ (see [1]). Limit Gibbs distributions $ p _ {\beta , \mu _ {1} , \dots, \mu _ {k} } ^ \infty $ are introduced on $ \Omega _ \infty $. They are constructed in a particular way by means of the Gibbs distributions (5) $ p _ {\beta , \mu _ {1} , \dots, \mu _ {k} } ^ {V} $ on finite systems (see [5], [9]). Although the introduction of infinite systems is a generally-accepted and fruitful method, it leads to complex intrinsic mathematical problems, which remain for the most part unsolved. These problems include, for example, the construction of a dynamics $ U _ {t} ^ \infty $, the construction of limit Gibbs distributions, studies on their properties, etc.
One of the main problems of statistical mechanics is the study of so-called phase transition, i.e. a sharp change of properties of a macroscopic system in a state of equilibrium, given a small change of the parameters describing this equilibrium — temperature, density of the particles, pressure, etc. In the modern mathematical approach, the problem of phase transition can be described in terms of limit Gibbs distributions in the following way: Given certain values of the parameters $ \beta , \mu _ {1}, \dots, \mu _ {k} $, it is possible, in general, to create a number of Gibbs distributions on $ \Omega _ \infty $ that are invariant relative to the action of the group $ T ^ {3} $ of shifts in $ \mathbf R ^ {3} $ (or of a subgroup $ G \subset T ^ {3} $ such that the quotient group $ T ^ {3} /G $ is compact), and are ergodic relative to this group (so-called pure phases). A point $ ( \beta , \mu _ {1}, \dots, \mu _ {k} ) $ of the parameter space is said to be regular if it has a sufficiently small neighbourhood in which the structure of the set of pure phases, and their basic qualitative properties (for example, the character of decrease of the correlations), remains unaltered. It is assumed that all numerical characteristics of these distributions (correlation functions, semi-invariants, etc.) in a neighbourhood of regular points depend analytically on the parameters $ \beta , \mu _ {1}, \dots, \mu _ {k} $. All other (not regular) points in the parameter space are also points of phase transition. Thus, either a sharp change in the structure of the Gibbs distributions (say a new phase disappears or arises) or in their properties (for example, decrease of the correlations changes from exponential to gradual) takes place at such points of the phase space. Each of the characteristics of the distribution, as a function of $ \beta , \mu _ {1} ,\dots, \mu _ {k} $, is considered to have a singularity at a point of phase transition. Describing the structure of phases and their properties for every concrete system, defining points of phase transition and the character of the singularities at these points, as well as other tasks, also constitute the problem of phase transition. Although a large class of model systems exists for which (at low temperatures) a number of general methods of solving this problem have been worked out (see [9]), the theory of phase transition is still far from being perfect. The study of the so-called critical points is particularly complex (roughly speaking, the fusion of various phases takes place at these points; see [10]), in that, at these points, the decrease of the correlations of the Gibbs distribution is very slow.
Many problems of statistical mechanics are related to the study of the time-development of distributions on a phase space, and particularly to the problem of relaxation, i.e. of approach to equilibrium. It is thought that, over a long period of time, every distribution on a phase space is approximated by an equilibrium (Gibbs) distribution. Despite the fact that many general representations of the mechanism of this process have been worked out, and that a number of simplified models have been studied, no complete theory exists yet (1991). The basic representations of the relaxation process (for the most part, they are still hypothetical) reduce to the fact that this process has three stages. At the first stage (while collisions of several particles are taking place), the distribution $ p _ {t} $ leads to a development of the system which is completely defined by a change of the first correlation function (i.e. by a distribution in a single-particle space $ X $). At the second stage — the kinetic stage, which lasts throughout the "free path" of the particle — the change of the first correlation function crosses over to a development in which everything depends only on the mean values of the particles, their speed, density, energy, etc. Lastly, there is the hydrodynamic stage, during which (as with macroscopic time) these mean values of density, speed, etc., are approximated by equilibrium values (see [11], [12]). Proving this scenario as a whole or in its separate parts is a complex mathematical problem, which is far from being completely solved (1991). Various systems of kinetic equations constitute a fundamental method of research. They are both exact, i.e. resulting directly from the definition of the Liouville equation (the hierarchical BBGKY chain — Bogolyubov, Born, Green, Kirkwood, Yvon) and approximate (the equations of Boltzmann, Chapman–Enskog, Vlasov–Landau, the hydrodynamic equations, etc.). These equations and their relation with the true picture of the evolution are also the subject of intensive mathematical study (cf. Bogolyubov chain of equations; Boltzmann equation; Chapman–Enskog method; Vlasov kinetic equation).
Quantum statistical mechanics is based on the same principles as classical mechanics. The quantum description of a system of particles located within a domain $ V $ requires that a Hilbert space $ {\mathcal H} _ {V} $ be given (the state space of the system), and that a self-adjoint operator $ H _ {V} $, operating on $ {\mathcal H} _ {V} $, be given (the energy operator of the system). The dynamics of the system is defined by the group $ U _ {t} ^ {V} = \mathop{\rm exp} \{ iH _ {V} \} $, $ t \in \mathbf R $, of unitary operators operating on $ {\mathcal H} _ {V} $, whereby the dynamics $ \{ {U _ {t} ^ {V} } : {t \in \mathbf R } \} $ generates a group of automorphisms $ W _ {t} ^ {V} $ of the algebra $ \mathfrak A ( {\mathcal H} _ {V} ) $ of bounded operators (observables) on $ {\mathcal H} _ {V} $:
$$ W _ {t} ^ {V} A = U _ {t} ^ {V} A( U _ {t} ^ {V} ) ^ {-1} . $$
The change to the statistical description in the quantum case plays a role in defining a certain "mean" $ \langle A\rangle $ on the algebra $ \mathfrak A ( {\mathcal H} _ {V} ) $, i.e. of a positive linear functional $ \rho ( A) = \langle A\rangle $ on this algebra, usually called a state. Every state on $ \mathfrak A ( {\mathcal H} _ {V} ) $ can be written in the form
$$ \rho ( A) = \mathop{\rm Sp} A \widetilde \rho , $$
where $ \rho $ is a positive nuclear operator from $ \mathfrak A ( {\mathcal H} _ {V} ) $ and $ \mathop{\rm Sp} \widetilde \rho = 1 $. The operator $ \widetilde \rho $ is usually called the density matrix of the state $ \rho $. The evolution in time of the state $ \rho $ is defined by the evolution $ W _ {t} ^ {V} $ of the algebra itself: $ \rho _ {t} ( A) = \rho (( W _ {t} ^ {V} ) ^ {-1} A) $. States that are invariant relative to this evolution are called equilibrium states, as before. For a system in which, apart from the energy $ H _ {V} = H _ {V} ^ {0} $, there are several pairwise-commuting integrals of motion $ H _ {V} ^ {1}, \dots, H _ {V} ^ {k} $, the equilibrium state with density matrix
$$ \widetilde \rho = Z ^ {-1} \ \mathop{\rm exp} \{ - \beta ( H _ {V} ^ {0} + \mu _ {1} H _ {V} ^ {1} + \dots + \mu _ {k} H _ {V} ^ {k} ) \} $$
is called a Gibbs state ( $ \beta > 0 $ and $ \mu _ {1}, \dots, \mu _ {k} $ are parameters, $ Z ^ {-1} $ is a normalizing factor). An infinite quantum system is introduced in the same way as for a classical system by passage to the thermodynamic limit $ V \uparrow \mathbf R ^ {3} $ (see [5]). In order to describe this system, the $ C ^ {*} $-algebra $ \mathfrak A _ \infty = {\cup _ {V \subset \mathbf R ^ {3} } \mathfrak A ( {\mathcal H} _ {V} ) } bar $ is examined (the bar signifies closure in the uniform topology), which is called the algebra of quasi-local observables, while the evolution $ W _ {t} ^ \infty $ in $ \mathfrak A _ \infty $ is defined as the limit of the evolutions $ W _ {t} ^ {V} $ on the finite algebras $ \mathfrak A ( {\mathcal H} _ {V} ) $. It is possible to introduce limit Gibbs states on the algebra $ \mathfrak A _ \infty $ in the same way as for classical systems (see [5]). The problem of phase transitions in quantum systems is formulated in the same way as for classical systems in terms of limit Gibbs states.
Finally, in quantum statistical mechanics there also exists a whole circle of kinetic problems; however, the mechanism of relaxation processes in quantum mechanics is more complicated than in classical mechanics, and is less studied.
There exist specific results on the so-called ground state of a system in the quantum case (corresponding to zero temperature) and on perturbations of this state of finite energy. A number of interesting problems is related to this problem (superconductivity, superfluidity), emerging at low temperatures [13]. Problems on the construction and study of quantum fields may be investigated by means of the theory of Gibbs fields, as developed in statistical mechanics (see [14], [15]).
References
| [1] | V.I. Arnol'd, "Mathematical methods of classical mechanics" , Springer (1978) (Translated from Russian) Zbl 0692.70003 Zbl 0572.70001 Zbl 0647.70001 |
| [2] | B.S. Nakhapetyan, "The central limit theorem for random fields with mixing property" R.L. Dobrushin (ed.) Ya.G. Sinai (ed.) , Multi-component random systems , M. Dekker (1980) pp. 531–547 (Translated from Russian) MR0599547 |
| [3] | I.P. [I.P. Kornfel'd] Cornfel'd, S.V. Fomin, Ya.G. Sinai, "Ergodic theory" , Springer (1982) (Translated from Russian) MR832433 |
| [4] | N.S. Krylov, "Works on the foundation of statistical physics" , Princeton Univ. Press (1979) (Translated from Russian) MR0551057 |
| [5] | D. Ruelle, "Statistical mechanics: rigorous results" , Benjamin (1966) MR0289084 Zbl 0997.82506 Zbl 1016.82500 Zbl 0177.57301 |
| [6] | A.M. [A.M. Khalfina] Halfina, "The limiting equivalence of the canonical and grand canonical ensembles (low density case)" Math. USSR Sb. , 9 : 1 (1969) pp. 1–52 Mat. Sb. , 80 (1969) pp. 3–51 |
| [7] | R.A. Minlos, A. Khaitov, "Limiting equivalence of thermodynamic ensembles in the case of one-dimensional systems" Trans. Moscow Math. Soc. , 32 (1975) pp. 143–180 Tr. Moskov. Mat. Obshch. , 32 (1975) pp. 147–186 MR416410 |
| [8] | O.E. Lanford, , Gibbs states in statistical physics , Moscow (1978) pp. 159–218 (In Russian; translated from English) |
| [9] | Ya.G. Sinai, "Theory of phase transitions: rigorous results" , Pergamon (1982) (Translated from Russian) MR0691854 |
| [10] | H.E. Stanley, "Phase transitions and critical phenomena" , Clarendon Press (1971) |
| [11] | R. Libov, "Introduction to the theory of kinetic equations" , Wiley (1969) |
| [12] | R. Balescu, "Equilibrium and non-equilibrium statistical mechanics" , 1–2 , Wiley (1975) MR0424103 MR0280130 |
| [13] | L.D. Landau, E.M. Lifshitz, "Statistical physics" , Pergamon (1980) (Translated from Russian) MR2730882 MR2559932 MR2226848 MR1917076 MR1781083 MR0954388 MR0560509 MR0674825 MR0242449 MR0183441 MR0136378 MR0056500 Zbl 1179.82002 Zbl 1095.82005 Zbl 1086.82001 Zbl 0993.00058 Zbl 0998.82504 Zbl 0859.76001 Zbl 0997.76500 Zbl 0659.76001 Zbl 0080.19702 Zbl 64.0887.01 |
| [14] | B. Simon, "The 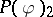 Euclidean (quantum) field theory" , Princeton Univ. Press (1974) Euclidean (quantum) field theory" , Princeton Univ. Press (1974) |
| [15] | , Euclidean quantum field theory. The Markov approach , Moscow (1978) (In Russian; translated from English) |
| [16] | J. Glimm, A. Jaffe, "Quantum physics, a functional integral point of view" , Springer (1981) Zbl 0461.46051 |
| [17] | V.A. Malyshev, R.A. Minlos, "Gibbs random fields" , Kluwer (1991) (Translated from Russian) MR1191166 Zbl 0731.60099 |
Comments
References
| [a1] | C. Cercignani, "The Boltzmann equation and its applications" , Springer (1988) MR1313028 Zbl 0646.76001 |
| [a2] | C. Cercignani, "Mathematical methods in kinetic theory" , Plenum (1990) MR1069558 Zbl 0726.76083 |
| [a3] | R.L. Dobrushin (ed.) , Mathematical problems of statistical mechanics and dynamics. A collection of surveys , Reidel (1986) MR0875429 Zbl 0596.00023 |
Statistical mechanics, mathematical problems in. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Statistical_mechanics,_mathematical_problems_in&oldid=52198