Smirnov class
The set  of all functions
of all functions  holomorphic in a simply-connected domain
holomorphic in a simply-connected domain  with rectifiable Jordan boundary
with rectifiable Jordan boundary  , such that for every function in it there is a sequence of closed rectifiable Jordan curves
, such that for every function in it there is a sequence of closed rectifiable Jordan curves  ,
,  with the following properties:
with the following properties:
1)  tends to
tends to  as
as  in the sense that if
in the sense that if  is the bounded domain with boundary
is the bounded domain with boundary  , then
, then
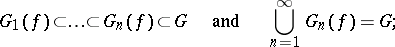 |
2)
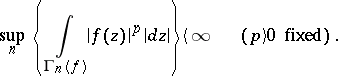 |
This definition was proposed by M.V. Keldysh and M.A. Lavrent'ev [2], and is equivalent to V.I. Smirnov's definition [1] in which curves  are used instead of
are used instead of  . These curves are the images of the circles
. These curves are the images of the circles 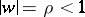 under some univalent conformal mapping
under some univalent conformal mapping  from the disc
from the disc  onto the domain
onto the domain  , and the supremum is taken over all
, and the supremum is taken over all  .
.
The classes  are the best known and most thoroughly studied generalization of the Hardy classes
are the best known and most thoroughly studied generalization of the Hardy classes  , and are connected with them by the following relation:
, and are connected with them by the following relation:  if and only if
if and only if
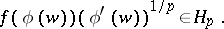 |
The properties of the classes  are closest to those of
are closest to those of 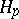 in the case when
in the case when  is a Smirnov domain. They have been generalized to domains
is a Smirnov domain. They have been generalized to domains 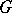 with boundaries of finite Hausdorff length. See also Boundary properties of analytic functions.
with boundaries of finite Hausdorff length. See also Boundary properties of analytic functions.
References
| [1] | V.I. Smirnov, "Sur les formules de Cauchy et de Green et quelques problèmes qui s'y rattachent" Izv. Akad. Nauk SSSR. Otdel. Mat. i Estestv. Nauk , 3 (1932) pp. 337–372 |
| [2] | M.V. Keldysh, M.A. Lavrent'ev, "Sur la répresentation conforme des domaines limités par des courbes rectifiables" Ann. Sci. Ecole Norm. Sup. , 54 (1937) pp. 1–38 |
| [3] | I.I. [I.I. Privalov] Priwalow, "Randeigenschaften analytischer Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) |
| [4] | G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian) |
| [5] | P.L. Duren, "Theory of 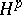 spaces" , Acad. Press (1970) spaces" , Acad. Press (1970) |
Smirnov class. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Smirnov_class&oldid=14423