Difference between revisions of "Slobodnik property"

Revision as of 17:25, 31 December 2016

Recall that a Baire space is a topological space in which every non-empty open subset is of the second category in itself (cf. also Category of a set). A space 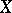is Baire if and only if the intersection of each countable family of dense open sets in 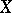is dense (cf. also Dense set).

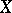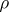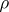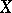In what follows, consider a space equipped with two topologies, and , and assume that is finer than . A topology has the Slobodnik property if the intersection of each countable family of -open -dense sets in is 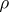-dense. If has the Slobodnik property, then 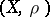is a Baire space. Following a definition of A.R. Todd from [a3], the topologies 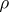and are 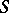-related if for any subset 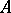of 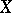, 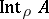(the interior of 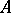with respect to the topology 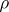) is non-empty if and only if 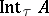is non-empty. 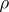If the topologies and are 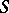-related, then has the Slobodnik property if and only if 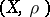is a Baire space, and this is the case if and only if 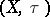is a Baire space.

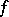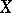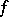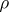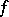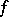Let be a function on of the first Baire class in the topology , i.e. is a pointwise limit of a sequence of -continuous functions (cf. also Baire classes). A very general problem emerges: How large can the set of all -continuity points of be? If has the Slobodnik property, then is 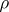-continuous at all points of 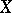except at a set of 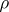-first category. This theorem generalizes Slobodnik's theorem from [a2]: Any limit of a sequence of separately continuous functions on the Euclidean space 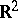is continuous on 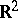, except at a set of the first category. Notice that separately continuous functions are of the first Baire class on 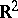, that a function 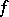is separately continuous on 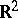exactly when it is continuous in the finer crosswise topology on 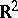(a set 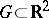is open in this topology if for any 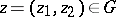there is a 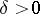such that the "cross"

is a subset of 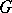), and that the crosswise topology has the Slobodnik property.

A more detailed investigation of the Slobodnik property and related notions can be found in [a1].

References

[a1]	J. Lukeš, J. Malý, L. Zajíček, "Fine topology methods in real analysis and potential theory" , Lecture Notes in Mathematics , 1189 , Springer (1986)
[a2]	S.G. Slobodnik, "Expanding system of linearly closed sets" Mat. Zametki , 19 (1976) pp. 61–84 (In Russian)
[a3]	A.R. Todd, "Quasiregular, pseudocomplete, and Baire spaces" Pacific J. Math. , 95 (1981) pp. 233–250

How to Cite This Entry:
Slobodnik property. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Slobodnik_property&oldid=40125

This article was adapted from an original article by J. LukeÅ¡ (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article

@@ Line 3: / Line 3: @@
 In what follows, consider a space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s1303803.png" /> equipped with two topologies, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s1303804.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s1303805.png" />, and assume that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s1303806.png" /> is finer than <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s1303807.png" />. A topology <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s1303808.png" /> has the Slobodnik property if the intersection of each countable family of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s1303809.png" />-open <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038010.png" />-dense sets in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038011.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038012.png" />-dense. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038013.png" /> has the Slobodnik property, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038014.png" /> is a Baire space. Following a definition of A.R. Todd from [[#References|[a3]]], the topologies <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038015.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038016.png" /> are <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038018.png" />-related if for any subset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038019.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038020.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038021.png" /> (the interior of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038022.png" /> with respect to the topology <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038023.png" />) is non-empty if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038024.png" /> is non-empty. If the topologies <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038025.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038026.png" /> are <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038027.png" />-related, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038028.png" /> has the Slobodnik property if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038029.png" /> is a Baire space, and this is the case if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038030.png" /> is a Baire space.
-Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038031.png" /> be a function on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038032.png" /> of the first Baire class in the topology <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038033.png" />, i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038034.png" /> is a pointwise limit of a sequence of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038035.png" />-continuous functions (cf. also [[Baire classes|Baire classes]]). A very general problem emerges: How large can the set of all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038036.png" />-continuity points of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038037.png" /> be? If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038038.png" /> has the Slobodnik property, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038039.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038040.png" />-continuous at all points of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038041.png" /> except at a set of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038042.png" />-first category. This theorem generalizes Slobodnik's theorem from [[#References|[a2]]]: Any limit of a sequence of separately continuous functions on the Euclidean space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038043.png" /> is continuous on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038044.png" />, except at a set of the first category. Notice that separately continuous functions are of the first Baire class on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038045.png" />, that a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038046.png" /> is separately continuous on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038047.png" /> exactly when it is continuous in the finer crosswise topology on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038048.png" /> (a set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038049.png" /> is open in this topology if for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038050.png" /> there is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038051.png" /> such that the  "cross"
+Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038031.png" /> be a function on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038032.png" /> of the first Baire class in the topology <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038033.png" />, i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038034.png" /> is a [[pointwise limit]] of a sequence of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038035.png" />-continuous functions (cf. also [[Baire classes|Baire classes]]). A very general problem emerges: How large can the set of all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038036.png" />-continuity points of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038037.png" /> be? If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038038.png" /> has the Slobodnik property, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038039.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038040.png" />-continuous at all points of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038041.png" /> except at a set of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038042.png" />-first category. This theorem generalizes Slobodnik's theorem from [[#References|[a2]]]: Any limit of a sequence of separately continuous functions on the Euclidean space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038043.png" /> is continuous on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038044.png" />, except at a set of the first category. Notice that separately continuous functions are of the first Baire class on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038045.png" />, that a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038046.png" /> is separately continuous on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038047.png" /> exactly when it is continuous in the finer crosswise topology on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038048.png" /> (a set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038049.png" /> is open in this topology if for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038050.png" /> there is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038051.png" /> such that the  "cross"
 <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130380/s13038052.png" /></td> </tr></table>

Navigation

Tools

Namespaces

Variants

Views

Actions

Difference between revisions of "Slobodnik property"

Revision as of 17:25, 31 December 2016

References