Slobodnik property
Recall that a Baire space is a topological space in which every non-empty open subset is of the second category in itself (cf. also Category of a set). A space 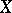 is Baire if and only if the intersection of each countable family of dense open sets in
is Baire if and only if the intersection of each countable family of dense open sets in 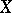 is dense (cf. also Dense set).
is dense (cf. also Dense set).
In what follows, consider a space 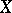 equipped with two topologies,
equipped with two topologies, 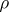 and
and  , and assume that
, and assume that  is finer than
is finer than 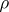 . A topology
. A topology  has the Slobodnik property if the intersection of each countable family of
has the Slobodnik property if the intersection of each countable family of  -open
-open  -dense sets in
-dense sets in 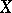 is
is 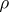 -dense. If
-dense. If  has the Slobodnik property, then
has the Slobodnik property, then 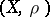 is a Baire space. Following a definition of A.R. Todd from [a3], the topologies
is a Baire space. Following a definition of A.R. Todd from [a3], the topologies 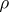 and
and  are
are 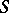 -related if for any subset
-related if for any subset 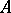 of
of 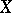 ,
, 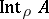 (the interior of
(the interior of 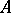 with respect to the topology
with respect to the topology 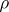 ) is non-empty if and only if
) is non-empty if and only if 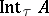 is non-empty. If the topologies
is non-empty. If the topologies  and
and 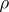 are
are 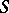 -related, then
-related, then  has the Slobodnik property if and only if
has the Slobodnik property if and only if 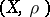 is a Baire space, and this is the case if and only if
is a Baire space, and this is the case if and only if 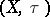 is a Baire space.
is a Baire space.
Let 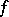 be a function on
be a function on 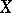 of the first Baire class in the topology
of the first Baire class in the topology  , i.e.
, i.e. 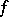 is a pointwise limit of a sequence of
is a pointwise limit of a sequence of  -continuous functions (cf. also Baire classes). A very general problem emerges: How large can the set of all
-continuous functions (cf. also Baire classes). A very general problem emerges: How large can the set of all 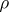 -continuity points of
-continuity points of 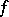 be? If
be? If  has the Slobodnik property, then
has the Slobodnik property, then 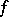 is
is 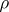 -continuous at all points of
-continuous at all points of 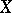 except at a set of
except at a set of 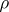 -first category. This theorem generalizes Slobodnik's theorem from [a2]: Any limit of a sequence of separately continuous functions on the Euclidean space
-first category. This theorem generalizes Slobodnik's theorem from [a2]: Any limit of a sequence of separately continuous functions on the Euclidean space 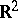 is continuous on
is continuous on 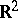 , except at a set of the first category. Notice that separately continuous functions are of the first Baire class on
, except at a set of the first category. Notice that separately continuous functions are of the first Baire class on 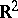 , that a function
, that a function 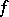 is separately continuous on
is separately continuous on 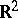 exactly when it is continuous in the finer crosswise topology on
exactly when it is continuous in the finer crosswise topology on 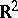 (a set
(a set 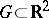 is open in this topology if for any
is open in this topology if for any 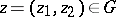 there is a
there is a 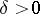 such that the "cross"
such that the "cross"
 |
is a subset of  ), and that the crosswise topology has the Slobodnik property.
), and that the crosswise topology has the Slobodnik property.
A more detailed investigation of the Slobodnik property and related notions can be found in [a1].
References
| [a1] | J. Lukeš, J. Malý, L. Zajíček, "Fine topology methods in real analysis and potential theory" , Lecture Notes in Mathematics , 1189 , Springer (1986) |
| [a2] | S.G. Slobodnik, "Expanding system of linearly closed sets" Mat. Zametki , 19 (1976) pp. 61–84 (In Russian) |
| [a3] | A.R. Todd, "Quasiregular, pseudocomplete, and Baire spaces" Pacific J. Math. , 95 (1981) pp. 233–250 |
Slobodnik property. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Slobodnik_property&oldid=12020