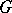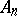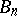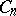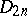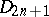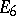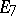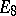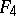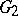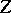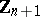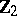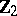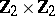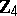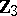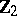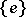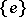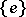Simply-connected group
A topological group (in particular, a Lie group) for which the underlying topological space is simply-connected. The significance of simply-connected groups in the theory of Lie groups is explained by the following theorems.
1) Every connected Lie group  is isomorphic to the quotient group of a certain simply-connected group (called the universal covering of
is isomorphic to the quotient group of a certain simply-connected group (called the universal covering of  ) by a discrete central subgroup isomorphic to
) by a discrete central subgroup isomorphic to  .
.
2) Two simply-connected Lie groups are isomorphic if and only if their Lie algebras are isomorphic; furthermore, every homomorphism of the Lie algebra of a simply-connected group  into the Lie algebra of an arbitrary Lie group
into the Lie algebra of an arbitrary Lie group  is the derivation of a (uniquely defined) homomorphism of
is the derivation of a (uniquely defined) homomorphism of  into
into  .
.
The centre  of a simply-connected semi-simple compact or complex Lie group
of a simply-connected semi-simple compact or complex Lie group  is finite. It is given in the following table for the various kinds of simple Lie groups.'
is finite. It is given in the following table for the various kinds of simple Lie groups.'
<tbody> </tbody>
|
In the theory of algebraic groups (cf. Algebraic group), a simply-connected group is a connected algebraic group  not admitting any non-trivial isogeny
not admitting any non-trivial isogeny 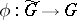 , where
, where 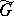 is also a connected algebraic group. For semi-simple algebraic groups over the field of complex numbers this definition is equivalent to that given above.
is also a connected algebraic group. For semi-simple algebraic groups over the field of complex numbers this definition is equivalent to that given above.
Comments
References
| [a1] | G. Hochschild, "The structure of Lie groups" , Holden-Day (1965) |
| [a2] | R. Hermann, "Lie groups for physicists" , Benjamin (1966) |
| [a3] | J.E. Humphreys, "Linear algebraic groups" , Springer (1975) pp. Sect. 35.1 |
Simply-connected group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Simply-connected_group&oldid=18749