Simple semi-group
A semi-group not containing proper ideals or congruences of some fixed type. Various kinds of simple semi-groups arise, depending on the type considered: ideal-simple semi-groups, not containing proper two-sided ideals (the term simple semi-group is often used for such semi-groups only); left (right) simple semi-groups, not containing proper left (right) ideals; (left, right)  -simple semi-groups, semi-groups with a zero not containing proper non-zero two-sided (left, right) ideals and not being two-element semi-groups with zero multiplication; bi-simple semi-groups, consisting of one
-simple semi-groups, semi-groups with a zero not containing proper non-zero two-sided (left, right) ideals and not being two-element semi-groups with zero multiplication; bi-simple semi-groups, consisting of one  -class (cf. Green equivalence relations);
-class (cf. Green equivalence relations);  -bi-simple semi-groups, consisting of two
-bi-simple semi-groups, consisting of two 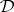 -classes one of which is the null class; and congruence-free semi-groups, not having congruences other than the universal relation and the equality relation.
-classes one of which is the null class; and congruence-free semi-groups, not having congruences other than the universal relation and the equality relation.
Every left or right simple semi-group is bi-simple; every bi-simple semi-group is ideal-simple, but there are ideal-simple semi-groups that are not bi-simple (and even ones for which all the 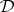 -classes consist of one element). The most important type of ideal-simple semi-groups (
-classes consist of one element). The most important type of ideal-simple semi-groups ( -simple semi-groups) are the completely-simple semi-groups (completely
-simple semi-groups) are the completely-simple semi-groups (completely  -simple semi-groups, cf. Completely-simple semi-group). The most important examples of bi-simple but not completely-simple semi-groups are: the bicyclic semi-groups and the four-spiral semi-group
-simple semi-groups, cf. Completely-simple semi-group). The most important examples of bi-simple but not completely-simple semi-groups are: the bicyclic semi-groups and the four-spiral semi-group 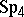 (cf. Bicyclic semi-group; [11]). The latter,
(cf. Bicyclic semi-group; [11]). The latter, 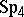 , is given by generators
, is given by generators 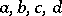 and defining relations
and defining relations 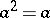 ,
,  ,
, 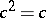 ,
, 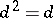 ,
, 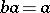 ,
, 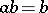 ,
, 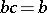 ,
, 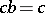 ,
, 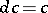 ,
, 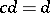 ,
, 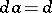 . It is isomorphic to a Rees semi-group of matrix type over a bicyclic semi-group with generators
. It is isomorphic to a Rees semi-group of matrix type over a bicyclic semi-group with generators 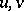 , where
, where 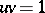 , with sandwich-matrix
, with sandwich-matrix
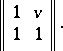 |
In a sense, 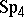 is minimal among the bi-simple not completely-simple semi-groups generated by a finite number of idempotents, and quite often it arises as a sub-semi-group of those semi-groups.
is minimal among the bi-simple not completely-simple semi-groups generated by a finite number of idempotents, and quite often it arises as a sub-semi-group of those semi-groups.
Right simple semi-groups are also called semi-groups with right division, or semi-groups with right invertibility. The reason for this terminology is the following equivalent property of such semi-groups: For any elements 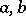 there is an
there is an  such that
such that 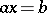 . The right simple semi-groups containing idempotents are precisely the right groups (cf. Right group). An important example of a right simple semi-group without idempotents is given by the semi-groups
. The right simple semi-groups containing idempotents are precisely the right groups (cf. Right group). An important example of a right simple semi-group without idempotents is given by the semi-groups 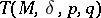 of all transformations
of all transformations 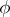 of a set
of a set 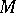 such that: 1) the kernel of
such that: 1) the kernel of 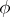 is the equivalence relation
is the equivalence relation 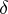 on
on  ; 2) the cardinality of the quotient set
; 2) the cardinality of the quotient set 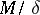 is
is 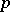 ; 3) the set
; 3) the set  intersects each
intersects each 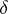 -class in at most one element; and 4) the set of
-class in at most one element; and 4) the set of 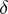 -classes disjoint from
-classes disjoint from 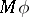 has infinite cardinality
has infinite cardinality 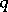 , and
, and 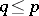 . The semi-group
. The semi-group 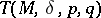 is called a Teissier semi-group of type
is called a Teissier semi-group of type 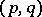 , and, if
, and, if 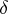 is the equality relation, it is called a Baer–Levi semi-group of type
is the equality relation, it is called a Baer–Levi semi-group of type 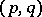 (cf. [6], [7]). A Teissier semi-group is an example of a right simple semi-group without idempotents that does not necessarily satisfy the right cancellation law. Every right simple semi-group without idempotents can be imbedded in a suitable Teissier semi-group, while every such semi-group with the right cancellation law can be imbedded in a suitable Baer–Levi semi-group (in both cases one can take
(cf. [6], [7]). A Teissier semi-group is an example of a right simple semi-group without idempotents that does not necessarily satisfy the right cancellation law. Every right simple semi-group without idempotents can be imbedded in a suitable Teissier semi-group, while every such semi-group with the right cancellation law can be imbedded in a suitable Baer–Levi semi-group (in both cases one can take  ).
).
Various types of simple semi-groups often arise as "blocks" from which one can construct the semi-groups under consideration. For classical examples of simple semi-groups see Completely-simple semi-group; Brandt semi-group; Right group; for bi-simple inverse semi-groups (including structure theorems under certain restrictions on the semi-lattice of idempotents) see [1], [8], [9]. There are ideal-simple inverse semi-groups with an arbitrary number of  -classes. In the study of imbedding of semi-groups in simple semi-groups one usually either indicates conditions for the possibility of the corresponding imbedding, or establishes that any semi-group can be imbedded in a semi-group of the type considered. E.g., any semi-group can be imbedded in a bi-simple semi-group with an identity (cf. [1]), in a bi-simple semi-group generated by idempotents (cf. [10]), and in a semi-group that is simple relative to congruences (which may have some property given in advance: the presence or absence of a zero, completeness, having an empty Frattini sub-semi-group, etc., cf. [3]–[5]).
-classes. In the study of imbedding of semi-groups in simple semi-groups one usually either indicates conditions for the possibility of the corresponding imbedding, or establishes that any semi-group can be imbedded in a semi-group of the type considered. E.g., any semi-group can be imbedded in a bi-simple semi-group with an identity (cf. [1]), in a bi-simple semi-group generated by idempotents (cf. [10]), and in a semi-group that is simple relative to congruences (which may have some property given in advance: the presence or absence of a zero, completeness, having an empty Frattini sub-semi-group, etc., cf. [3]–[5]).
References
| [1] | A.H. Clifford, G.B. Preston, "Algebraic theory of semi-groups" , 1–2 , Amer. Math. Soc. (1961–1967) |
| [2] | E.S. Lyapin, "Semigroups" , Amer. Math. Soc. (1974) (Translated from Russian) |
| [3] | L.A. Bokut', "Some embedding theorems for rings and semigroups" Sibirsk. Mat. Zh. , 4 : 3 (1963) pp. 500–518 (In Russian) |
| [4] | E.G. Shutov, "Embeddings of semigroups in simple and complete semigroups" Mat. Sb. , 62 : 4 (1963) pp. 496–511 (In Russian) |
| [5] | V.N. Klimov, "Embedding of semigroups in factorizable semigroups" Sib. Math. J. , 14 : 5 (1973) pp. 715–722 Sibirsk. Mat. Zh. , 14 : 5 (1973) pp. 1025–1036 |
| [6] | R. Baer, F. Levi, "Vollständige irreduzibele Systeme von Gruppenaxiomen" Sitzungsber. Heidelb. Akad. Wissenschaft. Math.-Nat. Kl. , 2 (1932) pp. 3–12 |
| [7] | M. Teissier, "Sur les demi-groupes admettant l'existence du quotient d'un cote" C.R. Acad. Sci. Paris , 236 : 11 (1953) pp. 1120–1122 |
| [8] | W.D. Munn, "Some recent results on the structure of inverse semigroups" K.W. Folley (ed.) , Semigroups , Acad. Press (1969) pp. 107–123 |
| [9] | J.M. Howie, "An introduction to semigroup theory" , Acad. Press (1976) |
| [10] | F. Pastijn, "Embedding semigroups in semibands" Semigroup Forum , 14 : 3 (1977) pp. 247–263 |
| [11] | K. Byleen, J. Meakin, F. Pastijn, "The fundamental four-spiral semigroup" J. of Algebra , 54 (1978) pp. 6–26 |
Simple semi-group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Simple_semi-group&oldid=18138