Selection theorems
A group of theorems in combinatorial theory related to the selection of elements from a set which in some way correspond to a family of subsets of that set. Selection theorems are commonly employed as existence theorems in solving various combinatorial problems. Below some of the most important selection theorems are listed, and examples of their application are given.
1) Let 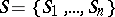 be some family of subsets of a given set
be some family of subsets of a given set 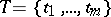 . A sample
. A sample 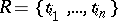 of distinct elements of the set
of distinct elements of the set 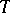 is called a system of distinct representatives (cf. System of different representatives) of the family
is called a system of distinct representatives (cf. System of different representatives) of the family 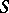 if
if 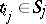 ,
, 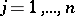 ; the element
; the element 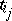 is a representative of the set
is a representative of the set 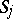 . For example, if
. For example, if 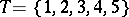 and
and 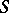 consists of
consists of 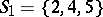 ,
, 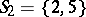 ,
, 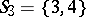 ,
, 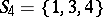 , then
, then 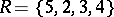 is a system of distinct representatives of
is a system of distinct representatives of 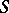 , where the element 5 represents the set
, where the element 5 represents the set 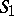 , the element 2 represents set
, the element 2 represents set 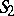 , etc. If, on the other hand,
, etc. If, on the other hand, 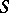 is composed of sets
is composed of sets 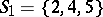 ,
, 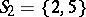 ,
, 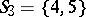 ,
,  ,
, 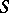 will have no system of distinct representatives, since
will have no system of distinct representatives, since 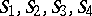 together contain only three elements.
together contain only three elements.
The theorem on a system of distinct representatives: A family  has a system of distinct representatives if and only if the union of any
has a system of distinct representatives if and only if the union of any 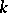 sets of
sets of 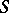 contains at least
contains at least 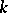 distinct elements, where
distinct elements, where 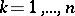 .
.
This theorem was proved by Ph. Hall [3] (see also [1], [2]). It may be used to prove the theorem on common representatives, which is also a selection theorem. Let
 | (1) |
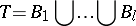 | (2) |
be two partitions of the set 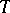 , i.e. none of the components is empty and
, i.e. none of the components is empty and 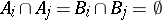 if
if 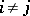 . The set
. The set 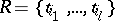 is called a system of common representatives of the partitions (1) and (2) if
is called a system of common representatives of the partitions (1) and (2) if 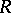 is a system of distinct representatives both for the family
is a system of distinct representatives both for the family 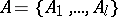 and the family
and the family 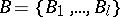 . For instance, if
. For instance, if  and if
and if
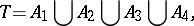 |
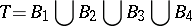 |
are two partitions of 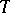 , where
, where 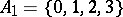 ,
, 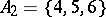 ,
, 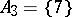 ,
, 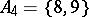 ,
, 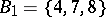 ,
, 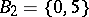 ,
, 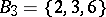 ,
, 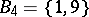 , then
, then 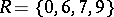 is a system of common representatives of the families
is a system of common representatives of the families 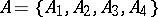 and
and 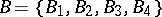 since it is a system of distinct representatives for both
since it is a system of distinct representatives for both 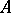 and
and 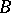 ; here the element 0 represents the sets
; here the element 0 represents the sets  and
and 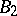 , the element 6 represents
, the element 6 represents 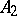 and
and 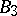 , the element 7 represents
, the element 7 represents 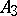 and
and  , while the element 9 represents
, while the element 9 represents 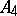 and
and 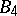 .
.
The theorem on a system of common representatives: The partitions (1) and (2) have a system of common representatives if and only if the union of any 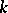 sets of
sets of 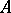 contains at most
contains at most 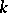 sets from the family
sets from the family 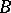 ,
,  [1], [2].
[1], [2].
2) Let there be given a rectangular matrix. The term line will denote both a row and a column of this matrix.
König's theorem: If the elements of a rectangular matrix are zeros and ones, the minimum number of lines containing all ones is equal to the maximum number of ones which may be selected so that no two of them are located on the same line.
This theorem was formulated and proved by D. König ([4], see also [1], [2]). It is equivalent to the Ph. Hall theorem. It is employed, for example, in order to prove that certain matrices are linear combinations of permutation matrices (a permutation matrix is a rectangular matrix 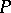 of dimension
of dimension 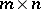 , consisting of zeros and ones, such that
, consisting of zeros and ones, such that 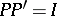 , where
, where  is the transposed matrix of
is the transposed matrix of  and
and 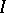 is the identity matrix of order
is the identity matrix of order 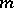 ; for example, a square permutation matrix of order
; for example, a square permutation matrix of order 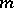 consists of
consists of 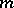 ones which are so disposed that no two of them lie on the same line). In other words, if a matrix
ones which are so disposed that no two of them lie on the same line). In other words, if a matrix 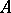 of dimension
of dimension 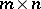 ,
, 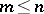 , has been given, with non-negative real numbers as its elements and such that the sum of the elements of each row in
, has been given, with non-negative real numbers as its elements and such that the sum of the elements of each row in  is
is 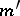 and the sum of the elements of each column is
and the sum of the elements of each column is 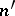 , then
, then
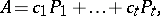 |
where each 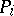 is a permutation matrix, while the coefficients
is a permutation matrix, while the coefficients 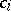 are non-negative real numbers [1], [2]. In particular, if a square matrix
are non-negative real numbers [1], [2]. In particular, if a square matrix 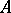 of order
of order  , consisting of zeros and ones, is such that the sum of the elements in any column or any row is equal to a positive integer
, consisting of zeros and ones, is such that the sum of the elements in any column or any row is equal to a positive integer 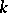 , then
, then
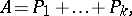 |
where all  are permutation matrices of order
are permutation matrices of order  .
.
Let 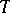 be a finite set and let
be a finite set and let 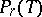 be the set of all its subsets containing exactly
be the set of all its subsets containing exactly  elements. Let
elements. Let
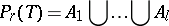 | (3) |
be an arbitrary ordered partition of 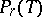 into
into  components
components  . Let
. Let 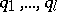 be integers such that
be integers such that
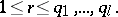 | (4) |
If there exists a subset, containing 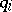 elements of the set
elements of the set 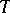 , such that all its subsets containing exactly
, such that all its subsets containing exactly  elements are contained in
elements are contained in  , it is said to be a
, it is said to be a 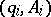 -subset of the set
-subset of the set 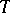 .
.
Ramsey's theorem: Let there be given integers 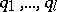 and
and  which satisfy condition (4). Then there exists a natural number
which satisfy condition (4). Then there exists a natural number 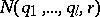 such that for any integer
such that for any integer 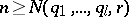 the following assertion is valid: Given a set
the following assertion is valid: Given a set 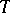 of
of  elements and an arbitrary ordered partition (3) of the set
elements and an arbitrary ordered partition (3) of the set 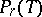 into
into 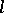 components
components  , then
, then 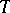 will contain a
will contain a 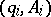 -subset for some
-subset for some 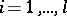 .
.
This theorem was proved by F. Ramsey [5]; see also [1], [2]. An example of an application of this theorem is the following result [6], [1], [2]: For any given integer 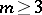 there exists an integer
there exists an integer 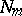 such that out of
such that out of 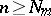 points in a plane no three of which lie on a straight line, there are
points in a plane no three of which lie on a straight line, there are 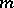 points which form a convex
points which form a convex  -gon.
-gon.
References
| [1] | M. Hall, "Combinatorial theory" , Blaisdell (1967) |
| [2] | H.J. Ryser, "Combinatorial mathematics" , Carus Math. Monogr. , 14 , Math. Assoc. Amer. (1963) |
| [3] | Ph. Hall, "On representatives of subsets" J. London Math. Soc. , 1 (1935) pp. 26–30 |
| [4] | D. König, "Theorie der endlichen und unendlichen Graphen" , Chelsea, reprint (1950) |
| [5] | F.P. Ramsey, "On a problem of formal logic" Proc. London Math. Soc. (2) , 30 (1930) pp. 264–286 |
| [6] | P. Erdös, G. Szekeres, "A combinatorial problem in geometry" Compositio Math. , 2 (1935) pp. 463–470 |
Comments
The popular name of the Ph. Hall theorem is marriage theorem or Ph. Hall marriage theorem.
An ordered partition of 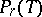 (as in (3)) can be regarded as a colouring of
(as in (3)) can be regarded as a colouring of 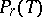 (with
(with 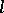 colours).
colours).
An important selection theorem is Rado's selection principle, see [a1]–[a3].
Selection problems and theorems arise in many parts of mathematics, not only combinatorics. The general setting is that of a set-valued mapping 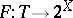 (where
(where  is the set of all subsets of
is the set of all subsets of  ) and the problem is to find a selection
) and the problem is to find a selection 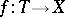 such that
such that 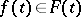 for all
for all 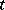 . Such a function
. Such a function 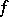 is sometimes called a selector.
is sometimes called a selector.
Note that the axiom of choice is an assertion about the existence of selections.
Further selection problems occur in topology, game theory, probability, measure theory, analysis, etc. A selection follows.
The Kuratowski–Ryll-Nardzweski selection theorem, [a1], says the following. Let 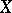 be a space with a
be a space with a 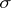 -algebra of subsets
-algebra of subsets 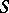 (cf. Algebra of sets) and let
(cf. Algebra of sets) and let 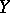 be a complete separable metric space. Let
be a complete separable metric space. Let 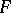 be a measurable set-valued function on
be a measurable set-valued function on  to the closed non-empty subsets of
to the closed non-empty subsets of 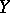 . Here, measurable means that
. Here, measurable means that 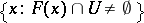 is in
is in  for every open
for every open 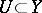 . Then there exists a measurable selector
. Then there exists a measurable selector 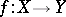 (i.e. such that
(i.e. such that 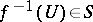 for every open
for every open  ).
).
The von Neumann measurable choice theorem, [a2], says essentially the following. Let 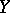 be a complete separable metric space and
be a complete separable metric space and 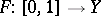 an analytic set-valued function. Then there is a Lebesgue-measurable selector
an analytic set-valued function. Then there is a Lebesgue-measurable selector 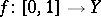 . Here, the set-valued function
. Here, the set-valued function 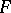 on
on 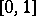 is called analytic if its graph
is called analytic if its graph 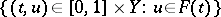 is an analytic subset of
is an analytic subset of 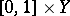 (cf. Analytic set).
(cf. Analytic set).
In topology there is, for example, Michael's continuous selection theorem, [a3], which characterizes paracompactness: A 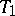 -space
-space 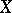 is paracompact if and only if every lower semi-continuous mapping
is paracompact if and only if every lower semi-continuous mapping 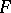 on
on  with values in the closed convex non-empty subsets of a Banach space
with values in the closed convex non-empty subsets of a Banach space 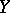 admits a continuous selector.
admits a continuous selector.
Cf. [a4], [a5] for some more selection theorems, more details and applications. For some other (variants of) selection theorems cf. also Multi-valued mapping. The phrase "selection theorem" is also used for various results pertaining e.g. to the selection of converging subsequences, cf. e.g. Helly theorem; Blaschke selection theorem; Bolzano–Weierstrass selection principle.
References
| [a1] | K. Kuratowski, C. Ryll-Nardzweski, "A general theorem on selectors" Bull. Acad. Pol. Sci., Ser. Math. Astron. Phys. , 13 (1965) pp. 397–403 |
| [a2] | J. von Neumann, "On rings of operators. Reduction theory" Ann. of Math. , 50 (1949) pp. 448–451 |
| [a3] | E. Michael, "Continuous selections I" Ann. of Math. , 63 (1956) pp. 361–382 |
| [a4] | T. Parthasarathy, "Selection theorems and their applications" , Lect. notes in math. , 263 , Springer (1972) |
| [a5] | W.M. Fleischman (ed.) , Set valued mappings, selections and topological properties of  (Proc. Conf. SUNY Buffalo, 1969) , Lect. notes in math. , 171 , Springer (1970) (Proc. Conf. SUNY Buffalo, 1969) , Lect. notes in math. , 171 , Springer (1970) |
| [a6] | L. Mirsky, "Transversal theory" , Acad. Press (1971) |
| [a7] | H. Lüneburg, "Tools and fundamental constructions of combinatorial mathematics" , B.I. Wissenschaftsverlag Mannheim (1989) |
| [a8] | R.L. Graham, B.L. Rothschild, J.H. Spencer, "Ramsey theory" , Wiley (Interscience) (1980) |
Selection theorems. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Selection_theorems&oldid=14987