Difference between revisions of "Schur functions in complex function theory"
m (AUTOMATIC EDIT (latexlist): Replaced 121 formulas out of 126 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
m (Automatically changed introduction) |
||
| Line 2: | Line 2: | ||
the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
was used. | was used. | ||
| − | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. |
Out of 126 formulas, 121 were replaced by TEX code.--> | Out of 126 formulas, 121 were replaced by TEX code.--> | ||
| − | {{TEX|semi-auto}}{{TEX| | + | {{TEX|semi-auto}}{{TEX|part}} |
The Schur class in complex analysis is the set of holomorphic functions $S ( z )$ which are defined and satisfy $| S ( z ) | \leq 1$ on the unit disc $\mathbf{D} = \{ z : | z | < 1 \}$ in the complex plane (cf. also [[Analytic function|Analytic function]]). The Schur class arises in diverse areas of classical analysis and operator theory, and it has applications in linear system theory and mathematical engineering. | The Schur class in complex analysis is the set of holomorphic functions $S ( z )$ which are defined and satisfy $| S ( z ) | \leq 1$ on the unit disc $\mathbf{D} = \{ z : | z | < 1 \}$ in the complex plane (cf. also [[Analytic function|Analytic function]]). The Schur class arises in diverse areas of classical analysis and operator theory, and it has applications in linear system theory and mathematical engineering. | ||
Revision as of 17:47, 1 July 2020
The Schur class in complex analysis is the set of holomorphic functions $S ( z )$ which are defined and satisfy $| S ( z ) | \leq 1$ on the unit disc $\mathbf{D} = \{ z : | z | < 1 \}$ in the complex plane (cf. also Analytic function). The Schur class arises in diverse areas of classical analysis and operator theory, and it has applications in linear system theory and mathematical engineering.
The Schur algorithm [a15] is an iterative construction that associates a sequence of complex numbers $\{ \gamma _ { n } \} _ { n = 0 } ^ { \infty }$ with a given function $S ( z )$ in the Schur class. The numbers are defined in terms of a sequence of Schur functions which is constructed recursively by setting $S _ { 0 } ( z ) = S ( z )$ and
\begin{equation*} S _ { n + 1 } ( z ) = \frac { 1 } { z } \frac { S _ { n } ( z ) - S _ { n } ( 0 ) } { 1 - \overline{S} _ { n } ( 0 ) S _ { n } ( z ) } , n \geq 0. \end{equation*}
If $| S _ { k } ( 0 ) | = 1$ for some $k$, $S _ { k } ( z )$ reduces to a constant and one sets $S _ { m } ( z ) \equiv 0$ for all $m > k$. The sequence $\gamma _ { n } = S _ { n } ( 0 )$, $n \geq 0$, thus consists of numbers of modulus at most one, and if some term of the sequence has unit modulus, all subsequent terms vanish; the numbers $\{ \gamma _ { n } \} _ { n = 0 } ^ { \infty }$ are called the Schur parameters of $S ( z )$. Every sequence of complex numbers of modulus at most one and having the property that if some term has unit modulus then all subsequent terms vanish, occurs as the Schur parameters of a unique function in the Schur class.
The Schur class plays a prominent role in classical moment and interpolation problems. One of the best known is the Schur problem, also known as the Carathéodory–Fejér problem: Find a Schur function $S ( z )$ whose first $n$ Taylor coefficients coincide with given numbers $S _ { 0 } , \ldots , S _ { n - 1 }$.
The Schur algorithm provides a means to describe all such functions because the first $n$ Schur parameters of a Schur function $S ( z )$ depend only on the first $n$ Taylor coefficients of $S ( z )$. A solution exists if and only if the matrix
\begin{equation*} \left( \begin{array} { c c c c } { S _ { 0 } } & { 0 } & { \ldots } & { 0 } \\ { S _ { 1 } } & { S _ { 0 } } & { \ldots } & { 0 } \\ { \vdots } & { \vdots } & { \ddots } & { \vdots } \\ { S _ { n - 1 } } & { S _ { n - 2 } } & { \ldots } & { S _ { 0 } } \end{array} \right) \end{equation*}
has norm at most one as an operator on $\mathbf{C} ^ { n }$ in the Euclidean metric. Similar results hold for the Nevanlinna–Pick problem: Find a Schur function $S ( z )$ such that $z _ { j } = S ( w _ { j } )$, $j = 1 , \ldots , n$, where $w _ { 1 } , \ldots , w _ { n }$ are given points in the unit disc and $z_1 , \dots ,z_n$ are complex numbers.
A solution to the Nevanlinna–Pick problem exists if and only if the matrix
\begin{equation*} \left( \frac { 1 - z _ { j } \overline {z} _ { k } } { 1 - w _ { j } \overline { w } _ { k } } \right) _ { j , k = 1 } ^ { n } \end{equation*}
is non-negative as an operator on $\mathbf{C} ^ { n }$ in the Euclidean metric. For example, see [a1], Chap. 3.
Many such classical problems are subsumed in abstract operator problems. There are several approaches in common use. To describe one approach, let $T$ be multiplication by a Schur function $S ( z )$ on the Hardy class $H ^ { 2 }$ for the unit disc (cf. also Hardy classes) [a7], and let $U$ be multiplication by $z$ on $H ^ { 2 }$. Then $T$ is a contraction which commutes with $U$, and every contraction on $H ^ { 2 }$ which commutes with $U$ has this form for some Schur function $S ( z )$. The commutation relation $T U = U T$ is preserved under compressions of $T$ and $U$ to certain subspaces of $H ^ { 2 }$. Let $\mathfrak{H}$ be an invariant subspace for $U ^ { * }$, and let $A = P T | _ { \mathfrak { H } }$ and $X = P U | _ { \mathfrak{H} }$, where $P$ is the projection of $H ^ { 2 }$ onto $\mathfrak{H}$. Then $A X = X A$. The Sarason generalized interpolation theorem [a5] asserts that every contraction $A$ on $\mathfrak{H}$ which commutes with $X$ has this form and is therefore associated with some Schur function $S ( z )$. Particular choices of the invariant subspace $\mathfrak{H}$ lead to solutions to the Schur and Nevanlinna–Pick problems. The generalized interpolation theorem has an abstract extension in the commutant lifting theorem [a8], p. 66, which extends the conclusion to arbitrary Hilbert space contraction operators $A \in \mathfrak { L } ( \mathfrak { H } _ { 1 } , \mathfrak { H } _ { 2 } )$, 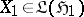 , and
, and 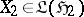 which are connected by a commutation relation $A X _ { 1 } = X _ { 2 } A$. In turn, the commutant lifting theorem is part of a broader theory of extensions and completions of Hilbert space operators [a14], which is motivated in part by connections with linear system theory and mathematical engineering [a11]. In such generalizations, scalar-valued functions are often replaced by matrix- or operator-valued functions. In tangential interpolation problems, only certain components of the data are specified. The approach of V.P. Potapov [a10] to tangential problems has diverse applications, as discussed, for example, in [a3]. See [a12] for realization theory. See [a16] for an overview of operator methods in interpolation theory.
which are connected by a commutation relation $A X _ { 1 } = X _ { 2 } A$. In turn, the commutant lifting theorem is part of a broader theory of extensions and completions of Hilbert space operators [a14], which is motivated in part by connections with linear system theory and mathematical engineering [a11]. In such generalizations, scalar-valued functions are often replaced by matrix- or operator-valued functions. In tangential interpolation problems, only certain components of the data are specified. The approach of V.P. Potapov [a10] to tangential problems has diverse applications, as discussed, for example, in [a3]. See [a12] for realization theory. See [a16] for an overview of operator methods in interpolation theory.
Schur functions arise in operator theory in other ways, such as in invariant subspace theory and its generalizations. For any Schur function $S ( z )$, the kernel $K_ S ( w , z ) = [ 1 - S ( z ) \overline { S ( w ) } ] / ( 1 - z \overline { w } )$ is non-negative on the unit disc in the sense that $\sum _ { i , j = 1 } ^ { n } \overline { c } _ { i } K _ { S } ( w _ { j } , w _ { i } ) c _ { j } \geq 0$ for all $w _ { 1 } , \dots , w _ { n } \in \mathbf{D}$, $c_1 , \ldots , c_n \in \mathbf{C}$, and $n \geq 1$. Therefore, $K _ { S } ( w , z )$ is the reproducing kernel for a Hilbert space $\mathfrak{H} ( S )$ of holomorphic functions on $\mathbf D$. The transformations
 |
are well defined, and the colligation
\begin{equation*} V = \left( \begin{array} { l l } { T } & { F } \\ { G } & { H } \end{array} \right) \end{equation*}
is co-isometric on $\mathfrak{H}(S)\oplus \mathbf{C}$, that is, $V V ^ { * } = 1$. The characteristic function of the colligation is $S ( z )$:
\begin{equation*} S ( z ) c = H c + z G ( 1 - z T ) ^ { - 1 } F c , c \in \mathbf{C}. \end{equation*}
The class of Hilbert space operators which are unitarily equivalent to a transformation $T$ which arises in this way from some Schur function can be characterized [a6], p. 39. Schur functions thus encode structural information for contraction operators. For example, the study of invariant subspaces is intimately related to factorizations $S ( z ) = S _ { 1 } ( z ) S _ { 2 } ( z )$ of a Schur function into a product of two Schur functions. The transformation $T$ is an example of a canonical model, that is, a concrete operator which is unitarily equivalent to an abstract operator of some prescribed type. A canonical model due to B. Sz.-Nagy and C. Foiaş is given in [a8]; see [a2] for a general notion of canonical model and operator-theoretic applications. Function-theoretic properties of a Schur function $S ( z )$, in turn, may be studied with the aid of model operators [a13].
More generally, a meromorphic function $S ( z )$, holomorphic in a subregion $\Omega$ of $D$ which contains the origin, is a generalized Schur function with $\kappa$ negative squares if the kernel $K _ { S } ( w , z )$ has $\kappa$ negative squares, that is, if every matrix 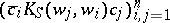 , where $w _ { 1 } , \dots , w _ { n } \in \Omega$, $c_1 , \ldots , c_n \in \mathbf{C}$, and $n \geq 1$, always has at most $\kappa$ negative eigenvalues, and at least one such matrix has exactly $\kappa$ negative eigenvalues [a9]. A space $\mathfrak{H} ( S )$ having reproducing kernel $K _ { S } ( w , z )$ exists now as a Pontryagin space. Transformations $T$, $F$, $G$, $H$ can be defined as before, giving rise to a co-isometric colligation $V$ in the same way. The main results of the Hilbert space theory have extensions to this situation [a4]. The indefinite theory has new elements. An example is the existence of a $\kappa$-dimensional non-positive invariant subspace for the contraction $T$ on $\mathfrak{H} ( S )$. The existence of such a subspace leads to the Krein–Langer factorization $S ( z ) = B ( z ) ^ { - 1 } S _ { 0 } ( z )$ for the generalized Schur function $S ( z )$. Here, $B ( z )$ is a Blaschke product having $\kappa$ factors and $S _ { 0 } ( z )$ belongs to the classical Schur class and is non-vanishing at the zeros of $B ( z )$. To say that $B ( z )$ is a Blaschke product of $\kappa$ factors means that it has the form
, where $w _ { 1 } , \dots , w _ { n } \in \Omega$, $c_1 , \ldots , c_n \in \mathbf{C}$, and $n \geq 1$, always has at most $\kappa$ negative eigenvalues, and at least one such matrix has exactly $\kappa$ negative eigenvalues [a9]. A space $\mathfrak{H} ( S )$ having reproducing kernel $K _ { S } ( w , z )$ exists now as a Pontryagin space. Transformations $T$, $F$, $G$, $H$ can be defined as before, giving rise to a co-isometric colligation $V$ in the same way. The main results of the Hilbert space theory have extensions to this situation [a4]. The indefinite theory has new elements. An example is the existence of a $\kappa$-dimensional non-positive invariant subspace for the contraction $T$ on $\mathfrak{H} ( S )$. The existence of such a subspace leads to the Krein–Langer factorization $S ( z ) = B ( z ) ^ { - 1 } S _ { 0 } ( z )$ for the generalized Schur function $S ( z )$. Here, $B ( z )$ is a Blaschke product having $\kappa$ factors and $S _ { 0 } ( z )$ belongs to the classical Schur class and is non-vanishing at the zeros of $B ( z )$. To say that $B ( z )$ is a Blaschke product of $\kappa$ factors means that it has the form
\begin{equation*} B ( z ) = C \prod _ { j = 1 } ^ { \kappa } \frac { z - \alpha_ j } { 1 - \overline { \alpha }_ j z }, \end{equation*}
where $\alpha _ { 1 } , \dots , \alpha _ { \kappa }$ are (not necessarily distinct) points of $\mathbf D$ and $C$ is a constant of unit modulus [a7]. The case $\kappa = 0$ is included by interpreting an empty product as one. Conversely, every function of the form $S ( z ) = B ( z ) ^ { - 1 } S _ { 0 } ( z )$ with $B ( z )$ and $S ( z )$ as above is a generalized Schur function, with $\kappa$ negative squares.
References
| [a1] | N.I. Akhiezer, "The classical moment problem" , Hafner (1965) |
| [a2] | N. Nikolski, V. Vasyunin, "Elements of spectral theory in terms of the free function model. I. Basic constructions" , Holomorphic spaces (Berkeley, CA, 1995) , Cambridge Univ. Press (1998) pp. 211–302 |
| [a3] | L.A. Sakhnovich, "Interpolation theory and its applications" , Kluwer Acad. Publ. (1997) |
| [a4] | D. Alpay, A. Dijksma, J. Rovnyak, H.S.V. de Snoo, "Reproducing kernel Pontryagin spaces" , Holomorphic spaces (Berkeley, CA, 1995) , Cambridge Univ. Press (1998) pp. 425–444 |
| [a5] | D. Sarason, "Generalized interpolation in $H ^ { \infty }$" Trans. Amer. Math. Soc. , 127 (1967) pp. 179–203 |
| [a6] | L. de Branges, J. Rovnyak, "Square summable power series" , Holt, Rinehart&Winston (1966) |
| [a7] | P.L. Duren, "Theory of $H ^ { p }$ spaces" , Acad. Press (1970) |
| [a8] | B. Sz.-Nagy, C. Foiaş, "Harmonic analysis of operators on Hilbert space" , North-Holland (1970) |
| [a9] | M.G. Krein, H. Langer, "Über einige Fortsetzungsprobleme, die eng mit der Theorie hermitescher Operatoren im Raume $\Pi _ { \kappa }$ zusammenhängen. I. Einige Funktionenklassen und ihre Darstellungen" Math. Nachr. , 77 (1977) pp. 187–236 |
| [a10] | V.P. Potapov, "Collected papers" , Hokkaido Univ. Research Inst. Applied Electricity, Division Appl. Math., Sapporo (1982) (Edited and transl. by T. Ando) |
| [a11] | T. Kailath, "A theorem of I. Schur and its impact on modern signal processing" , I. Schur methods in operator theory and signal processing , Oper. Th. Adv. Appl. , 18 , Birkhäuser (1986) pp. 9–30 |
| [a12] | J.A. Ball, I. Gohberg, L. Rodman, "Interpolation of rational matrix functions" , Oper. Th. Adv. Appl. , 45 , Birkhäuser (1990) |
| [a13] | D. Sarason, "Sub-Hardy Hilbert spaces in the unit disk" , Wiley (1994) |
| [a14] | C. Foias, A.E. Frazho, I. Gohberg, M.A. Kaashoek, "Metric constrained interpolation, commutant lifting and systems" , Oper. Th. Adv. Appl. , 100 , Birkhäuser (1998) |
| [a15] | I. Schur, "Über Potenzreihen, die im Innern des Einheitskreises beschränkt sind. I-II" J. Reine Angew. Math. , 147–148 (1917-1918) pp. 205–232; 122–145 (Also: Gesammelte Abh. II, no. 29–30. English transl.: I. Schur methods in operator theory and signal processing, Vol. 18 of Oper. Th. Adv. Appl., Birkhäuser, 1986, pp. 31–59; 61–88) |
| [a16] | H. Dym, "The commutant lifting approach to interpolation problems, by Ciprian Foias and Arthur E. Frazho (book review)" Bull. Amer. Math. Soc. , 31 (1994) pp. 125–140 |
Schur functions in complex function theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Schur_functions_in_complex_function_theory&oldid=50850