S-integer
As a simple example, let 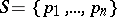 be a finite set of rational prime numbers. The rational integers
be a finite set of rational prime numbers. The rational integers 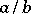 ,
,  , relatively prime (cf. also Mutually-prime numbers), such that the set of prime divisors of
, relatively prime (cf. also Mutually-prime numbers), such that the set of prime divisors of 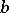 (possibly empty) is contained in
(possibly empty) is contained in 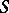 are the so-called
are the so-called 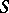 -integers (corresponding to the specific set
-integers (corresponding to the specific set 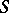 ). Clearly, this is a subring
). Clearly, this is a subring  of
of  . Let
. Let  denote the group of units of
denote the group of units of 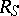 , i.e. the group of multiplicatively invertible elements of
, i.e. the group of multiplicatively invertible elements of 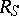 (the
(the 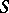 -units). Clearly, these are
-units). Clearly, these are 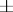 and the rational numbers
and the rational numbers  in the prime decomposition of which only prime numbers from the set
in the prime decomposition of which only prime numbers from the set 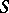 appear.
appear.
These notions can be defined in a more sophisticated way, the advantage of which is that it can be generalized to the more general case of a number field. For this the notion of absolute value on a number field is needed. Unfortunately, there is no general agreement on the definition of this notion. Below, this "absolute value" is taken in the sense of a metric as in [a1], Chap. 1, Sect. 4; Chap. 4, Sect. 4; equivalently, an absolute value is a function  , where
, where 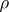 is a fixed, conveniently chosen positive real number
is a fixed, conveniently chosen positive real number 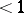 and
and  is a valuation, as defined and used in [a2], Chap. 1, § 2; Chap. 3 § 1, (cf. also Valuation, which gives a slightly different definition).
is a valuation, as defined and used in [a2], Chap. 1, § 2; Chap. 3 § 1, (cf. also Valuation, which gives a slightly different definition).
In the special case above, every rational prime number 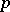 gives rise to a
gives rise to a 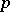 -adic absolute value and all possible absolute values of
-adic absolute value and all possible absolute values of 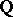 are (up to topological equivalence) the
are (up to topological equivalence) the 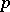 -adic ones (non-Archimedean), denoted by
-adic ones (non-Archimedean), denoted by 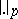 , and the usual absolute value (Archimedean), denoted by
, and the usual absolute value (Archimedean), denoted by 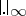 . Let
. Let 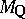 denote the set of absolute values (more precisely, the set of equivalence classes of absolute values (i.e. places) of
denote the set of absolute values (more precisely, the set of equivalence classes of absolute values (i.e. places) of 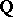 ; cf. also Place of a field). Thus, every element of this set is of the form
; cf. also Place of a field). Thus, every element of this set is of the form 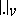 , where
, where  is either a rational prime number or the symbol
is either a rational prime number or the symbol 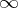 . One now modifies the definition of the set
. One now modifies the definition of the set 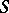 above as the subset of
above as the subset of 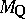 containing the absolute values (i.e. places)
containing the absolute values (i.e. places) 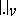 , where
, where 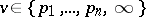 . Then
. Then 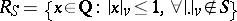 and
and 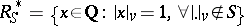 .
.
Consider now the more general situation, where a number field  is taken in place of
is taken in place of 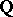 and its ring of integers
and its ring of integers 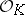 is taken in place of
is taken in place of 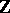 . Let
. Let 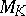 be the set of absolute values of
be the set of absolute values of  (more precisely, the set of equivalence classes of absolute values, i.e. places, of
(more precisely, the set of equivalence classes of absolute values, i.e. places, of 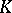 ). These are divided into two categories, namely, the non-Archimedean ones, which are in one-to-one correspondence with the prime ideals (or, what is essentially the same, with the prime divisors) of
). These are divided into two categories, namely, the non-Archimedean ones, which are in one-to-one correspondence with the prime ideals (or, what is essentially the same, with the prime divisors) of 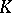 and the Archimedean ones, which are in one-to-one correspondence with the isomorphic embeddings
and the Archimedean ones, which are in one-to-one correspondence with the isomorphic embeddings 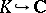 (complex-conjugate embeddings giving rise to the same absolute value). As before, let
(complex-conjugate embeddings giving rise to the same absolute value). As before, let 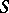 be a finite subset of
be a finite subset of 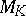 containing all Archimedean valuations of
containing all Archimedean valuations of 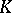 . Then, the set
. Then, the set 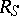 of
of 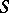 -integers and the set
-integers and the set 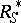 of
of 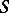 -units are defined exactly as in the case of rational numbers (see the definitions above), where now
-units are defined exactly as in the case of rational numbers (see the definitions above), where now  is replaced by
is replaced by  .
.
Many interesting problems concerning the solution of Diophantine equations are reduced to questions about 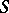 -integers of "particularly simple form" (e.g. linear forms in two unknown parameters), which are
-integers of "particularly simple form" (e.g. linear forms in two unknown parameters), which are 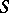 -units, and then results are obtained by applying a variety of relevant results on
-units, and then results are obtained by applying a variety of relevant results on 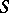 -integers and
-integers and 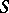 -units.
-units.
References
| [a1] | Z.I. Borevich, I.R. Shafarevich, "Number Theory" , Acad. Press (1966) (In Russian) |
| [a2] | W. Narkiewicz, "Elementary and analytic theory of algebraic numbers" , PWN/Springer (1990) |
S-integer. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=S-integer&oldid=15023