Roses (curves)
Planar curves whose equations in polar coordinates have the form
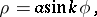 |
where  and
and  are constants. If
are constants. If 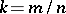 is a rational number, then a rose is an algebraic curve of even order.
is a rational number, then a rose is an algebraic curve of even order.
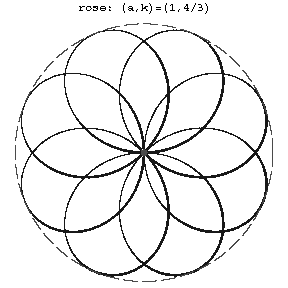
Figure: r082610a
The order of a rose is equal to 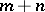 if
if 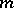 and
and  are odd, and to
are odd, and to 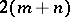 if either
if either 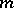 or
or  is even. The entire curve is situated inside the circle of radius
is even. The entire curve is situated inside the circle of radius  and consists of congruent parts, called petals (see Fig.). If
and consists of congruent parts, called petals (see Fig.). If 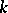 is an integer, then the rose consists of
is an integer, then the rose consists of 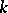 petals for
petals for 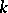 odd and of
odd and of 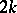 petals for
petals for 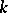 even. If
even. If 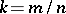 and
and 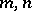 are relatively prime, then the rose consists of
are relatively prime, then the rose consists of 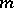 petals for
petals for 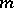 and
and  odd, and of
odd, and of 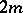 petals when either
petals when either 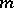 or
or  is even.
is even.
When 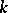 is irrational there are infinitely many petals. Roses belong to the family of cycloidal curves (cf. Cycloidal curve). They are hypocycloids if
is irrational there are infinitely many petals. Roses belong to the family of cycloidal curves (cf. Cycloidal curve). They are hypocycloids if 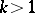 , and epicycloids if
, and epicycloids if 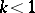 .
.
Roses are also related to the family of cycloidal curves by the fact that they are pedals of epi- and hypocycloids with respect to the centre of their fixed circle.
The arc length of a rose is given by an elliptic integral of the second kind. The area of one petal is 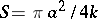 .
.
Roses are also called curves of Guido Grandi, who was the first to describe them in 1728.
References
| [1] | A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian) |
Comments
These curves are also called rhodoneas, cf. [a1].
References
| [a1] | J.D. Lawrence, "A catalog of special plane curves" , Dover, reprint (1972) |
| [a2] | F. Gomes Teixeira, "Traité des courbes" , 1–3 , Chelsea, reprint (1971) |
Roses (curves). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Roses_(curves)&oldid=16994