Reproducing kernel
Consider an abstract set 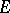 and a linear set
and a linear set 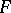 of functions
of functions 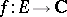 .
.
Assume that 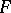 is equipped with an inner product
is equipped with an inner product 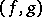 and
and 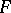 is complete with respect to the norm
is complete with respect to the norm 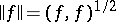 . Then
. Then 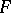 is a Hilbert space.
is a Hilbert space.
A function 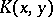 ,
, 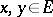 , is called a reproducing kernel of such a Hilbert space
, is called a reproducing kernel of such a Hilbert space 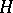 if and only if the following two conditions are satisfied:
if and only if the following two conditions are satisfied:
i) for every fixed 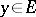 , the function
, the function 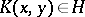 ;
;
ii)  ,
, 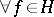 .
.
This definition is given in [a1]; see also [a6].
Some properties of reproducing kernels are:
1) If a reproducing kernel 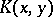 exists, then it is unique.
exists, then it is unique.
2) A reproducing kernel 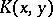 exists if and only if
exists if and only if 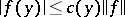 ,
, 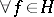 , where
, where 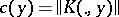 .
.
3)  is a non-negative-definite kernel, that is,
is a non-negative-definite kernel, that is,
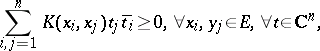 |
where the overbar stands for complex conjugation.
In particular, 3) implies:
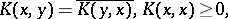 |
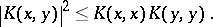 |
Every non-negative-definite kernel 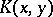 generates a Hilbert space
generates a Hilbert space 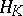 for which
for which 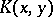 is a reproducing kernel (see also Reproducing-kernel Hilbert space).
is a reproducing kernel (see also Reproducing-kernel Hilbert space).
If  is a reproducing kernel, then the operator
is a reproducing kernel, then the operator 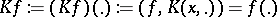 is injective:
is injective: 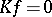 implies
implies 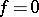 , by reproducing property ii), and
, by reproducing property ii), and 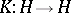 is surjective (cf. also Injection; Surjection). Therefore the inverse operator
is surjective (cf. also Injection; Surjection). Therefore the inverse operator 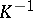 is defined on
is defined on 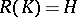 , and since
, and since 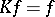 , the operator
, the operator 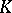 is the identity operator on
is the identity operator on 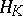 , and so is its inverse.
, and so is its inverse.
Examples of reproducing kernels.
Consider the Hilbert space 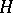 of analytic functions (cf. Analytic function) in a bounded simply-connected domain
of analytic functions (cf. Analytic function) in a bounded simply-connected domain 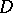 of the complex
of the complex  -plane. If
-plane. If 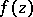 is analytic in
is analytic in  ,
, 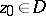 , and the disc
, and the disc 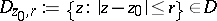 , then
, then
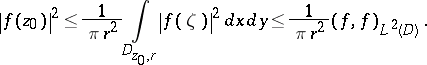 |
Therefore 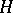 is a reproducing-kernel Hilbert space. Its reproducing kernel
is a reproducing-kernel Hilbert space. Its reproducing kernel 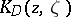 is called the Bergman kernel (cf. also Bergman kernel function).
is called the Bergman kernel (cf. also Bergman kernel function).
If 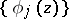 is an orthonormal basis of
is an orthonormal basis of  (cf. also Orthogonal system; Basis),
(cf. also Orthogonal system; Basis), 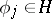 , then
, then 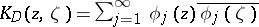 .
.
If 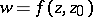 is the conformal mapping of
is the conformal mapping of 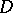 onto the disc
onto the disc 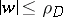 , such that
, such that 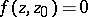 ,
, 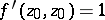 , then [a2]:
, then [a2]:
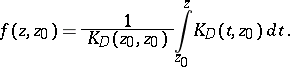 |
Let 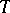 be a domain in
be a domain in 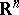 and
and 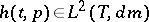 for every
for every 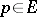 . Here
. Here 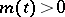 is a finite measure on
is a finite measure on 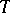 .
.
Define a linear mapping 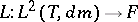 by
by
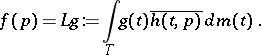 | (a1) |
Define the kernel
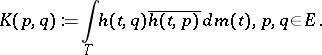 | (a2) |
This kernel is non-negative-definite:
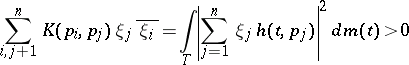 |
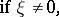 |
provided that for any set  the set of functions
the set of functions  is linearly independent in
is linearly independent in 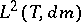 (cf. Linear independence).
(cf. Linear independence).
In this case the kernel 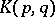 generates a uniquely determined reproducing-kernel Hilbert space
generates a uniquely determined reproducing-kernel Hilbert space 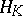 for which
for which 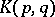 is the reproducing kernel.
is the reproducing kernel.
In [a6] it is claimed that a convenient characterization of the range 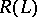 of the linear transformation (a1) is given by the formula
of the linear transformation (a1) is given by the formula  . In [a4] it is shown by examples that such a characterization is often useless in practice: in general the norm in
. In [a4] it is shown by examples that such a characterization is often useless in practice: in general the norm in 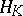 can not be described in terms of the standard Sobolev or Hölder norms, and the assumption in [a6] that
can not be described in terms of the standard Sobolev or Hölder norms, and the assumption in [a6] that 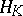 can be realized as
can be realized as 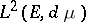 is not justified and is not correct, in general.
is not justified and is not correct, in general.
However, in [a6] there are some examples of characterizations of  for some special operators
for some special operators 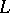 and in [a5] a characterization of the range of a wide class of multi-dimensional linear transforms, whose kernels are kernels of positive rational functions of self-adjoint elliptic operators, is given.
and in [a5] a characterization of the range of a wide class of multi-dimensional linear transforms, whose kernels are kernels of positive rational functions of self-adjoint elliptic operators, is given.
Reproducing kernels are discussed in [a5] for rigged triples of Hilbert spaces (cf. also Rigged Hilbert space). If 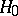 is a Hilbert space and
is a Hilbert space and 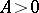 is a linear compact operator defined on all of
is a linear compact operator defined on all of 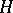 , then the closure of
, then the closure of 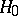 in the norm
in the norm 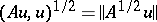 is a Hilbert space
is a Hilbert space 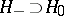 . The space dual to
. The space dual to 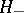 , with respect to
, with respect to 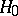 , is denoted by
, is denoted by 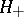 ,
, 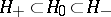 . The inner product in
. The inner product in 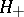 is given by the formula
is given by the formula 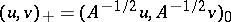 . The space
. The space 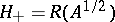 , equipped with this inner product, is a Hilbert space.
, equipped with this inner product, is a Hilbert space.
Let 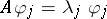 , where the eigenvalues
, where the eigenvalues  are counted according to their multiplicities and
are counted according to their multiplicities and 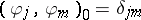 , where
, where 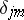 is the Kronecker delta.
is the Kronecker delta.
Assume that 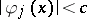 for all
for all 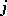 and all
and all  , and
, and 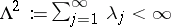 .
.
Then 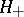 is a reproducing-kernel Hilbert space and its reproducing kernel is
is a reproducing-kernel Hilbert space and its reproducing kernel is  .
.
To check that 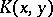 is indeed the reproducing kernel of
is indeed the reproducing kernel of 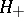 , one calculates
, one calculates 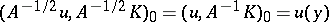 . Indeed,
. Indeed,  is the identity operator because
is the identity operator because 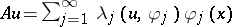 , so that
, so that 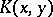 is the kernel of the operator
is the kernel of the operator 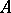 in
in 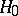 .
.
The value 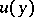 is a linear functional in
is a linear functional in 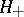 , so that
, so that 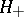 is a reproducing-kernel Hilbert space. Indeed, if
is a reproducing-kernel Hilbert space. Indeed, if 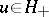 , then
, then  . Therefore, denoting
. Therefore, denoting 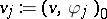 and using the Cauchy inequality and Parseval equality one gets:
and using the Cauchy inequality and Parseval equality one gets:
 |
as claimed.
From the representation of the inner product in the reproducing-kernel Hilbert space 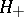 by the formula
by the formula 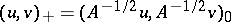 it is clear that, in general, the inner product in
it is clear that, in general, the inner product in 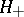 is not an inner product in
is not an inner product in 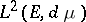 .
.
The inner product in 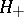 is of the form
is of the form
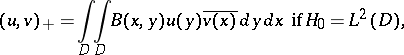 |
where the distributional kernel 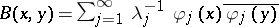 acts on
acts on 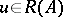 by the formula
by the formula 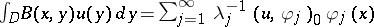 , where
, where 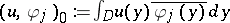 is the Fourier coefficient of
is the Fourier coefficient of  (cf. also Fourier coefficients). If
(cf. also Fourier coefficients). If 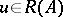 , then
, then 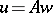 for some
for some 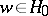 , and
, and 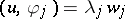 . Thus, the series
. Thus, the series  converges in
converges in 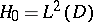 .
.
References
| [a1] | N. Aronszajn, "Theory of reproducing kernels" Trans. Amer. Math. Soc. , 68 (1950) pp. 337–404 |
| [a2] | S. Bergman, "The kernel function and conformal mapping" , Amer. Math. Soc. (1950) |
| [a3] | A.G. Ramm, "On the theory of reproducing kernel Hilbert spaces" J. Inverse Ill-Posed Probl. , 6 : 5 (1998) pp. 515–520 |
| [a4] | A.G. Ramm, "On Saitoh's characterization of the range of linear transforms" A.G. Ramm (ed.) , Inverse Problems, Tomography and Image Processing , Plenum (1998) pp. 125–128 |
| [a5] | A.G. Ramm, "Random fields estimation theory" , Longman/Wiley (1990) |
| [a6] | S. Saitoh, "Integral transforms, reproducing kernels and their applications" , Pitman Res. Notes , Longman (1997) |
| [a7] | L. Schwartz, "Sous-espaces hilbertiens d'espaces vectoriels topologique et noyaux associes" Anal. Math. , 13 (1964) pp. 115–256 |
Reproducing kernel. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Reproducing_kernel&oldid=16915