Representation of a semi-group
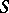 in a class of semi-groups
in a class of semi-groups 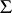
A homomorphism of 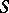 into a semi-group from
into a semi-group from 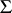 (in the case of an injective homomorphism one speaks of a faithful representation). One usually has in mind a class of concrete semi-groups. Representations in a class of transformation semi-groups (for short — representations by transformations, cf. also Transformation semi-group), in a class of semi-groups of partial transformations or binary relations, or in a class of matrix semi-groups (so-called matrix, or linear, representations of a semi-group) have been studied most completely. In automata theory, with each automaton one associates a representation of the free semi-group of transformations of the set of its internal states. Representations of a semi-group by transformations that are in some way or other related to properties of the elements of the transformed set, endowed with some structure, (endomorphisms, continuous transformations, etc.) have special significance. Every semi-group with an identity element can be isomorphically represented as the semi-group of all endomorphisms of an oriented or non-oriented graph, as the semi-group of all endomorphisms of an algebra with unary operations, etc. A few constructions for obtaining all representations of a semi-group by partial transformations are known (1983). These representations are constructed from certain simple representations by union, multiple repetition, restriction to a subset, and by the operation of imbedding of semi-groups.
(in the case of an injective homomorphism one speaks of a faithful representation). One usually has in mind a class of concrete semi-groups. Representations in a class of transformation semi-groups (for short — representations by transformations, cf. also Transformation semi-group), in a class of semi-groups of partial transformations or binary relations, or in a class of matrix semi-groups (so-called matrix, or linear, representations of a semi-group) have been studied most completely. In automata theory, with each automaton one associates a representation of the free semi-group of transformations of the set of its internal states. Representations of a semi-group by transformations that are in some way or other related to properties of the elements of the transformed set, endowed with some structure, (endomorphisms, continuous transformations, etc.) have special significance. Every semi-group with an identity element can be isomorphically represented as the semi-group of all endomorphisms of an oriented or non-oriented graph, as the semi-group of all endomorphisms of an algebra with unary operations, etc. A few constructions for obtaining all representations of a semi-group by partial transformations are known (1983). These representations are constructed from certain simple representations by union, multiple repetition, restriction to a subset, and by the operation of imbedding of semi-groups.
By adjoining an identity element to a semi-group 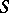 ,
,  , and by extending the regular representation of
, and by extending the regular representation of  by left shifts onto a Cartesian power
by left shifts onto a Cartesian power 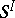 of
of 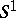 , one obtains a representation
, one obtains a representation 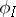 — the
— the  -fold repetition of the regular representation of
-fold repetition of the regular representation of  . Every representation
. Every representation 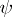 of
of 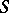 by transformations of a set
by transformations of a set  can be obtained (cf. [2]) from
can be obtained (cf. [2]) from 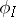 by means of a mapping
by means of a mapping 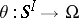 such that
such that
 |
Transitive representations (i.e. representations 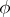 by transformations of a set
by transformations of a set  such that for any
such that for any 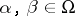 there is an
there is an  for which
for which 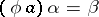 ) play a special role.
) play a special role.
The representations of a semi-group are, by one-to-one partial transformations, related to the notion and properties of inverse semi-groups (cf. Inversion semi-group).
For the study of matrix representations of a semi-group one invokes semi-group algebras (cf. Semi-group algebra). The problem of reducibility of matrix representations has been studied. For a number of semi-groups (including finite semi-groups) the irreducible representations (cf. Irreducible representation) have been found. The matrix representations of completely-simple and completely  -simple semi-groups (cf. Completely-simple semi-group) can be constructed as extensions of representations of their subgroups. The matrix representations of arbitrary semi-groups can be described by means of representations of their factors, which are simple and
-simple semi-groups (cf. Completely-simple semi-group) can be constructed as extensions of representations of their subgroups. The matrix representations of arbitrary semi-groups can be described by means of representations of their factors, which are simple and  -simple semi-groups.
-simple semi-groups.
References
| [1] | A.H. Clifford, G.B. Preston, "Algebraic theory of semi-groups" , 1–2 , Amer. Math. Soc. (1961–1967) |
| [2] | V.V. Vagner, "Representations of ordered semi-groups" Mat. Sb. , 38 : 2 (1956) pp. 203–240 (In Russian) |
| [3] | E.S. Lyapin, "Representations of semi-groups by partial mappings" Mat. Sb. , 52 : 1 (1960) pp. 589–596 (In Russian) |
| [4] | B.M. Shain, "Representations of semi-groups by binary relations" Mat. Sb. , 60 : 3 (1963) pp. 293–303 (In Russian) |
| [5a] | D.B. McAlister, "Representations of semigroups by linear transformations I" Semi-group Forum , 2 : 3 (1971) pp. 189–263 |
| [5b] | D.B. McAlister, "Representations of semigroups by linear transformations II" Semi-group Forum , 2 : 4 (1971) pp. 283–320 |
| [6] | B. Jónsson, "Topics in universal algebra" , Springer (1972) |
Representation of a semi-group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Representation_of_a_semi-group&oldid=16867