Regular torus
An algebraic torus in a connected algebraic group  (over an algebraically closed field) that is contained in only a finite number of Borel subgroups (cf. Borel subgroup). The maximal tori in
(over an algebraically closed field) that is contained in only a finite number of Borel subgroups (cf. Borel subgroup). The maximal tori in  are always regular (cf. Maximal torus). In general, a torus
are always regular (cf. Maximal torus). In general, a torus  is regular if and only if its centralizer
is regular if and only if its centralizer  is a solvable group. One-dimensional regular tori
is a solvable group. One-dimensional regular tori  and their corresponding one-parameter subgroups
and their corresponding one-parameter subgroups  (also called regular) play an important role in algebraic group theory. A torus that is not regular is called singular. For reductive groups
(also called regular) play an important role in algebraic group theory. A torus that is not regular is called singular. For reductive groups  (cf. Reductive group), a criterion for the singularity of a torus
(cf. Reductive group), a criterion for the singularity of a torus  can be given in terms of root systems. Thus, if
can be given in terms of root systems. Thus, if  is a maximal torus in
is a maximal torus in 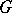 containing
containing 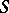 and
and 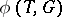 is the corresponding root system, then
is the corresponding root system, then  is singular if and only if
is singular if and only if  for some
for some 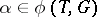 .
.
A regular torus in 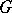 is sometimes defined as a torus
is sometimes defined as a torus 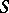 that contains a regular element (an element
that contains a regular element (an element  is regular if the dimension of the centralizer
is regular if the dimension of the centralizer 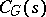 in
in 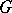 is minimal), and it is then called a semi-regular torus if it is regular in the sense of the original definition (see, for example, [1]). Both these definitions are equivalent for reductive groups.
is minimal), and it is then called a semi-regular torus if it is regular in the sense of the original definition (see, for example, [1]). Both these definitions are equivalent for reductive groups.
References
| [1] | A. Borel, "Linear algebraic groups" , Benjamin (1969) |
| [2] | J.E. Humphreys, "Linear algebraic groups" , Springer (1975) |
Regular torus. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Regular_torus&oldid=18431