Regular semi-group
A semi-group in which every element is regular (see Regular element).
An arbitrary regular semi-group 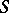 contains idempotents (see Idempotent), and the structure of
contains idempotents (see Idempotent), and the structure of 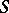 is determined to a considerable extent by the "structure" and the "distribution" in
is determined to a considerable extent by the "structure" and the "distribution" in 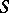 of the set
of the set 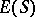 of all its idempotents (cf. Idempotents, semi-group of). Regular semi-groups with a unique idempotent are just groups. In the first place,
of all its idempotents (cf. Idempotents, semi-group of). Regular semi-groups with a unique idempotent are just groups. In the first place, 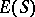 can be regarded as a partially ordered set in a natural way. There are known structure theorems describing a regular semi-group
can be regarded as a partially ordered set in a natural way. There are known structure theorems describing a regular semi-group 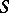 with certain natural restrictions on the set
with certain natural restrictions on the set 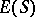 . One such restriction (for semi-groups with zero) is that all non-zero idempotents are primitive (see Completely-simple semi-group); a semi-group with this property is called primitive. The following conditions on a semi-group
. One such restriction (for semi-groups with zero) is that all non-zero idempotents are primitive (see Completely-simple semi-group); a semi-group with this property is called primitive. The following conditions on a semi-group  are equivalent: a)
are equivalent: a) 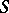 is a primitive regular semi-group; b)
is a primitive regular semi-group; b) 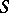 is a regular semi-group equal to the union of its
is a regular semi-group equal to the union of its  -minimal (right) ideals (see Minimal ideal); and c)
-minimal (right) ideals (see Minimal ideal); and c) 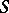 is an
is an 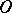 -direct union of completely
-direct union of completely  -simple semi-groups. The structure of regular semi-groups is also known in the case when
-simple semi-groups. The structure of regular semi-groups is also known in the case when 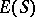 is a chain with the order type of the negative integers [2].
is a chain with the order type of the negative integers [2].
A more informative view of  is obtained if one defines a partial operation
is obtained if one defines a partial operation  on it in the following way. If
on it in the following way. If 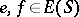 are such that at least one of the products
are such that at least one of the products 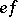 ,
, 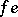 is equal to either
is equal to either  or
or 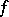 , then
, then 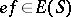 ; one then sets
; one then sets 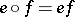 . The resulting partial algebra can be axiomatized in terms of two quasi-order relations
. The resulting partial algebra can be axiomatized in terms of two quasi-order relations 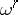 and
and 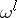 . These are closely related to the given partial operation (the realization of these relations in
. These are closely related to the given partial operation (the realization of these relations in 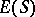 is as follows:
is as follows: 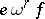 means
means 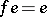 ,
,  means
means 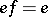 ; then
; then 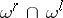 is the natural partial order on
is the natural partial order on 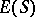 ). Such a partial algebra is called a bi-ordered set (see [5]). An arbitrary regular semi-group can be constructed in a specific way from a bi-ordered set and groups. It is thus possible to classify regular semi-groups in terms of bi-ordered sets. Among the types of semi-groups that have been investigated in this way are combinatorial regular semi-groups (see [7]), that is, those whose only subgroups consist of one element.
). Such a partial algebra is called a bi-ordered set (see [5]). An arbitrary regular semi-group can be constructed in a specific way from a bi-ordered set and groups. It is thus possible to classify regular semi-groups in terms of bi-ordered sets. Among the types of semi-groups that have been investigated in this way are combinatorial regular semi-groups (see [7]), that is, those whose only subgroups consist of one element.
A homomorphic image of a regular semi-group is regular. Every normal complex of a regular semi-group which is a sub-semi-group contains an idempotent. An arbitrary congruence (cf. Congruence (in algebra)) on a regular semi-group is uniquely determined by its classes that contain idempotents. A congruence on a regular semi-group 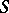 separates idempotents if and only if it is contained in the relation
separates idempotents if and only if it is contained in the relation 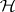 (see Green equivalence relations). The set of such congruences forms a modular sublattice with a zero and a unit element in the lattice of all congruences on
(see Green equivalence relations). The set of such congruences forms a modular sublattice with a zero and a unit element in the lattice of all congruences on  (cf. also Modular lattice). A regular semi-group is called fundamental if this sublattice contains only the equality relation. Every combinatorial regular semi-group is fundamental. Fundamental regular semi-groups are important, not only as one of the more visible types of regular semi-groups, but also because of their "universality" property in the class of all semi-groups. More precisely, for any bi-ordered set
(cf. also Modular lattice). A regular semi-group is called fundamental if this sublattice contains only the equality relation. Every combinatorial regular semi-group is fundamental. Fundamental regular semi-groups are important, not only as one of the more visible types of regular semi-groups, but also because of their "universality" property in the class of all semi-groups. More precisely, for any bi-ordered set 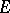 it is possible to construct in a canonical way a fundamental regular semi-group
it is possible to construct in a canonical way a fundamental regular semi-group  such that
such that 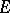 is the bi-ordered set of all idempotents, and for any regular semi-group
is the bi-ordered set of all idempotents, and for any regular semi-group 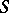 with
with 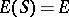 there is a homomorphism
there is a homomorphism 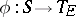 that separates idempotents and is such that
that separates idempotents and is such that 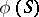 is a sub-semi-group of
is a sub-semi-group of 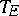 containing
containing 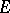 (for various constructions of
(for various constructions of  , see [3], [5], [8], [10]). A regular semi-group
, see [3], [5], [8], [10]). A regular semi-group 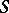 is fundamental if and only if
is fundamental if and only if 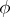 is injective.
is injective.
If 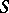 is a regular semi-group, then the sub-semi-group
is a regular semi-group, then the sub-semi-group 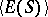 generated by its idempotents is also regular. The sub-semi-group
generated by its idempotents is also regular. The sub-semi-group 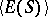 exerts an essential influence on the structure of
exerts an essential influence on the structure of 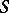 . A regular semi-group is idempotently generated if and only if the same is true for each of its principal factors [10]. In an idempotently-generated regular semi-group
. A regular semi-group is idempotently generated if and only if the same is true for each of its principal factors [10]. In an idempotently-generated regular semi-group 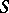 , any element
, any element  can be written in the form
can be written in the form 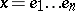 , where
, where 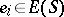 and
and 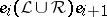 for
for  (here
(here 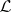 and
and 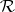 are Green equivalence relations, [5]). A sequence of idempotents
are Green equivalence relations, [5]). A sequence of idempotents  with the above property is called an
with the above property is called an 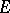 -chain. In a bi-simple idempotently-generated semi-group, any two idempotents are connected by an
-chain. In a bi-simple idempotently-generated semi-group, any two idempotents are connected by an 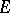 -chain, and if they are comparable in the sense of the natural partial order, then such a chain has length
-chain, and if they are comparable in the sense of the natural partial order, then such a chain has length 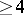 .
.
If 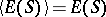 , that is, the product of any two idempotents is again an idempotent, then the regular semi-group
, that is, the product of any two idempotents is again an idempotent, then the regular semi-group 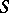 is called orthodox. The class of orthodox semi-groups contains, in particular, all inverse semi-groups. A semi-group is orthodox if and only if its principal factors are. There are structure theorems for orthodox semi-groups (see [4], [9]).
is called orthodox. The class of orthodox semi-groups contains, in particular, all inverse semi-groups. A semi-group is orthodox if and only if its principal factors are. There are structure theorems for orthodox semi-groups (see [4], [9]).
The natural partial order on 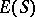 can be extended to the regular semi-group
can be extended to the regular semi-group 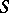 in the following way:
in the following way: 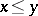 if there are idempotents
if there are idempotents  and
and 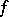 such that
such that 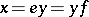 . If
. If  is inverse, the relation
is inverse, the relation 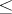 becomes the natural partial order, and it is also called the natural partial order for an arbitrary regular semi-group. The relation
becomes the natural partial order, and it is also called the natural partial order for an arbitrary regular semi-group. The relation 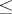 on the regular semi-group
on the regular semi-group 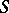 is compatible with the multiplication if and only if, for any idempotent
is compatible with the multiplication if and only if, for any idempotent  , the sub-semi-group
, the sub-semi-group 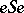 is inverse [6] (cf. Inversion semi-group). Regular semi-groups with this property are called pseudo-inverse. A wider class is formed by pseudo-orthodox semi-groups (those in which the sub-semi-group
is inverse [6] (cf. Inversion semi-group). Regular semi-groups with this property are called pseudo-inverse. A wider class is formed by pseudo-orthodox semi-groups (those in which the sub-semi-group  is orthodox for any idempotent
is orthodox for any idempotent  ). These classes of semi-groups are also called "locally inverse regular semi-grouplocally inverse" and "locally orthodox regular semi-grouplocally orthodox" , respectively. A regular semi-group is called natural if the set of all its group elements (see Regular element) is a sub-semi-group. There are structure theorems for pseudo-inverse, pseudo-orthodox [11] and natural [12] regular semi-groups.
). These classes of semi-groups are also called "locally inverse regular semi-grouplocally inverse" and "locally orthodox regular semi-grouplocally orthodox" , respectively. A regular semi-group is called natural if the set of all its group elements (see Regular element) is a sub-semi-group. There are structure theorems for pseudo-inverse, pseudo-orthodox [11] and natural [12] regular semi-groups.
Numerous structure theorems for various types of regular semi-groups represent (sometimes very remote) generalizations and modifications of the structure of a Rees semi-group of matrix type or of the sum of the direct spectrum of groups (see Clifford semi-group), and are based on various representations of semi-groups and their decomposition into subdirect products (see [1], [13]). See also Semi-group.
References
| [1] | A.H. Clifford, G.B. Preston, "Algebraic theory of semi-groups" , 1–2 , Amer. Math. Soc. (1961–1967) |
| [2] | W.D. Munn, "Regular  -semigroups" Glasgow Math. J. , 9 : 1 (1968) pp. 46–66 -semigroups" Glasgow Math. J. , 9 : 1 (1968) pp. 46–66 |
| [3] | A. Clifford, "The fundamental representation of a regular semigroup" Semigroup Forum , 10 (1975) pp. 84–92 |
| [4] | A. Clifford, "A structure theorem for orthogroups" J. Pure Appl. Algebra , 8 (1976) pp. 23–50 |
| [5] | K.S.S. Nambooripad, "Structure of regular semigroups, I" Mem. Amer. Math. Soc. , 22 : 224 (1979) |
| [6] | K.S.S. Nambooripad, "The natural partial order on a regular semigroup" Proc. Edinburgh Math. Soc. , 23 : 3 (1980) pp. 249–260 |
| [7] | K.S.S. Nambooripad, A.R. Rajan, "Structure of combinatorial regular semigroups" Quart. J. Math. , 29 : 116 (1978) pp. 489–504 |
| [8] | P.A. Grillet, "The structure of regular semigroups, I-IV" Semigroup Forum , 8 (1974) pp. 177–183; 254–265; 368–373 |
| [9] | T.E. Hall, "Orthodox semigroups" Pacific. J. Math. , 39 (1971) pp. 677–686 |
| [10] | T.E. Hall, "On regular semigroups" J. of Algebra , 24 (1973) pp. 1–24 |
| [11] | J. Meakin, K.S.S. Nambooripad, "Coextensions of pseudo-inverse semigroups by rectangular bands" J. Austral. Math. Soc. , 30 (1980/81) pp. 73–86 |
| [12] | R.J. Warne, "Natural regular semigroups" G. Pollák (ed.) , Algebraic Theory of Semigroups , North-Holland (1979) pp. 685–720 |
| [13] | G. Lallement, "Structure theorems for regular semigroups" Semigroup Forum , 4 (1972) pp. 95–123 |
Regular semi-group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Regular_semi-group&oldid=13668