Regular scheme

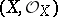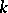A scheme such that at every point the local ring is regular (cf. Regular ring (in commutative algebra)). For schemes of finite type over an algebraically closed field , regularity is equivalent to the sheaf of differentials 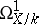being locally free. Regular local rings are factorial (cf. Factorial ring), and so any closed reduced irreducible subscheme of codimension 1 in a regular scheme 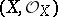is given locally by one equation (see [2]). An important problem is the construction of a regular scheme 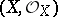with a given field 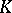of rational functions and equipped with a proper morphism 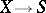onto some base scheme 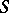. The solution is known in the case when 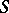is the spectrum of a field of characteristic 0 (see [3]), and for schemes of low dimension in the case of a prime characteristic and also in the case when 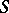is the spectrum of a Dedekind domain with 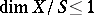(see [1]).

References

[1]	S.S. Abhyankar, "On the problem of resolution of singularities" I.G. Petrovskii (ed.) , Proc. Internat. Congress Mathematicians Moscow, 1966 , Moscow (1968) pp. 469–481
[2]	D. Mumford, "Lectures on curves on an algebraic surface" , Princeton Univ. Press (1966)
[3]	H. Hironaka, "Resolution of singularities of an algebraic variety over a field of characteristic zero I, II" Ann. of Math. , 79 (1964) pp. 109–203; 205–326

Comments

Sometimes a regular scheme is called a smooth scheme, in which case one means that the structure morphism 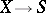is a smooth morphism (where 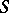is the spectrum of a field, cf. Spectrum of a ring).

References

[a1]	R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. 111–115; 126