Reflective subcategory
A subcategory which contains a "largest" model of any object of a given category. More precisely, a full subcategory 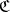 of a category
of a category 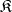 is called reflective if it contains a reflection (cf. Reflection of an object of a category) for every object of
is called reflective if it contains a reflection (cf. Reflection of an object of a category) for every object of 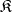 . Equivalently,
. Equivalently, 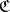 is reflective in
is reflective in 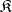 if and only if the inclusion functor
if and only if the inclusion functor  has a left adjoint
has a left adjoint  . The functor
. The functor 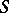 sends each object
sends each object 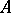 of
of 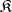 to its
to its 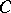 -reflection
-reflection 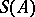 ; the morphisms
; the morphisms 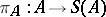 appearing in the definition of a reflection constitute a natural transformation from the identity functor on
appearing in the definition of a reflection constitute a natural transformation from the identity functor on  to the composite of
to the composite of 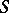 with the inclusion functor, which is the unit of the adjunction (see Adjoint functor). The concept dual to that of a reflective subcategory is called a coreflective subcategory.
with the inclusion functor, which is the unit of the adjunction (see Adjoint functor). The concept dual to that of a reflective subcategory is called a coreflective subcategory.
A reflective subcategory 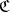 inherits many properties from the ambient category
inherits many properties from the ambient category 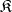 . For example, a morphism
. For example, a morphism  of
of 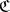 is a monomorphism in
is a monomorphism in 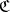 if and only if it is a monomorphism in
if and only if it is a monomorphism in 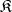 . Therefore, every reflective subcategory of a well-powered category is well-powered. A reflective subcategory is closed under products, to the extent that they exist in the ambient category. The same holds for more general limits. A reflective subcategory need not be closed under colimits, but the functor
. Therefore, every reflective subcategory of a well-powered category is well-powered. A reflective subcategory is closed under products, to the extent that they exist in the ambient category. The same holds for more general limits. A reflective subcategory need not be closed under colimits, but the functor 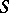 transforms colimits in
transforms colimits in 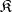 into colimits in
into colimits in 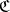 . Thus, a reflective subcategory of a complete (cocomplete) category is complete (cocomplete).
. Thus, a reflective subcategory of a complete (cocomplete) category is complete (cocomplete).
Suppose 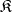 is complete and has a bicategory (factorization) structure in which every object has only a set of admissible quotients. Then every full subcategory
is complete and has a bicategory (factorization) structure in which every object has only a set of admissible quotients. Then every full subcategory 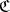 of
of 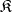 which is closed under products and admissible subobjects is reflective. In this context, one may construct the
which is closed under products and admissible subobjects is reflective. In this context, one may construct the 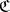 -reflection of an object
-reflection of an object 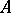 of
of 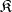 as follows: Choose a set of representatives
as follows: Choose a set of representatives 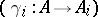 ,
, 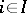 , of those quotient objects of
, of those quotient objects of 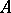 which lie in
which lie in 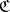 . The product
. The product 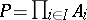 belongs to
belongs to 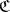 , and the
, and the 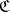 -reflection
-reflection 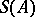 is the image of the unique morphism
is the image of the unique morphism 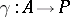 such that
such that  ,
, 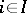 .
.
Examples.
1) Let 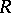 be an integral domain. The full subcategory of torsion-free injective modules is reflective in the category of all torsion-free
be an integral domain. The full subcategory of torsion-free injective modules is reflective in the category of all torsion-free 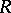 -modules; the reflections are the injective hulls of torsion-free modules. In particular, the full subcategory of divisible torsion-free Abelian groups is reflective in the category of torsion-free Abelian groups.
-modules; the reflections are the injective hulls of torsion-free modules. In particular, the full subcategory of divisible torsion-free Abelian groups is reflective in the category of torsion-free Abelian groups.
2) The full subcategory of compact Hausdorff topological spaces is reflective in the category of completely regular topological spaces. The Stone–Čech compactification provides the reflector.
3) The category of sheaves on a topological space is reflective in the category of pre-sheaves. The reflector is defined by the associated sheaf functor (sheafication).
Comments
A few authors extend the use of the term "reflective subcategory" to include non-full subcategories for which the inclusion functor has a left adjoint.
A reflective subcategory is called epireflective if the canonical morphism  is an epimorphism for every
is an epimorphism for every 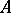 . If every morphism in
. If every morphism in 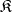 factors as an epimorphism followed by a monomorphism, then a reflective subcategory of
factors as an epimorphism followed by a monomorphism, then a reflective subcategory of 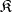 will be epireflective provided it is closed under arbitrary subobjects in
will be epireflective provided it is closed under arbitrary subobjects in 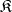 . The three examples listed in the main article are not epireflective, but (for example) the category of Abelian groups is epireflective in the category of all groups. The dual concept is that of a monocoreflective subcategory; for example, the category of torsion Abelian groups is monocoreflective in the category of all Abelian groups.
. The three examples listed in the main article are not epireflective, but (for example) the category of Abelian groups is epireflective in the category of all groups. The dual concept is that of a monocoreflective subcategory; for example, the category of torsion Abelian groups is monocoreflective in the category of all Abelian groups.
Reflective subcategory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Reflective_subcategory&oldid=14303