Difference between revisions of "Ramanujan sums"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | r0772201.png | ||
| + | $#A+1 = 21 n = 1 | ||
| + | $#C+1 = 21 : ~/encyclopedia/old_files/data/R077/R.0707220 Ramanujan sums | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | Trigonometric sums depending on two integer parameters $ k $ | |
| + | and $ n $: | ||
| − | + | $$ | |
| + | c _ {k} ( n) = \sum _ { h } | ||
| + | \mathop{\rm exp} | ||
| + | \left ( | ||
| − | + | \frac{2 \pi n h i }{k} | |
| − | + | \right ) = \ | |
| + | \sum _ { h } \cos | ||
| + | \frac{2 \pi n h }{k} | ||
| + | , | ||
| + | $$ | ||
| − | Ramanujan sums are | + | when $ h $ |
| + | runs over all non-negative integers less than $ k $ | ||
| + | and relatively prime to $ k $. | ||
| + | The basic properties of Ramanujan sums are multiplicity with respect to the index $ k $, | ||
| + | |||
| + | $$ | ||
| + | c _ {k k ^ \prime } ( n) = c _ {k} ( n) c _ {k ^ \prime } ( n) \ \ | ||
| + | \textrm{ if } ( k , k ^ \prime ) = 1 , | ||
| + | $$ | ||
| + | |||
| + | and also the representation in terms of the [[Möbius function|Möbius function]] $ \mu $: | ||
| + | |||
| + | $$ | ||
| + | c _ {k} ( n) = \ | ||
| + | \sum _ {d \mid ( k , n ) } \mu \left ( | ||
| + | \frac{k}{d} | ||
| + | \right ) d . | ||
| + | $$ | ||
| + | |||
| + | Ramanujan sums are finite if $ k $ | ||
| + | or $ n $ | ||
| + | is finite. In particular, $ c _ {k} ( 1) = 1 $. | ||
Many multiplicative functions on the natural numbers (cf. [[Multiplicative arithmetic function|Multiplicative arithmetic function]]) can be expanded as series of Ramanujan sums, and, conversely, the basic properties of Ramanujan sums enable one to sum series of the form | Many multiplicative functions on the natural numbers (cf. [[Multiplicative arithmetic function|Multiplicative arithmetic function]]) can be expanded as series of Ramanujan sums, and, conversely, the basic properties of Ramanujan sums enable one to sum series of the form | ||
| − | + | $$ | |
| + | \sum _ { n= } 1 ^ \infty | ||
| + | |||
| + | \frac{c _ {k} ( q n ) }{n ^ {s} } | ||
| + | f ( n) ,\ \ | ||
| + | \sum _ { k= } 1 ^ \infty | ||
| + | |||
| + | \frac{c _ {k} ( q n ) }{k ^ {s} } | ||
| + | f ( k) , | ||
| + | $$ | ||
| + | |||
| + | where $ f $ | ||
| + | is a multiplicative function and $ q $ | ||
| + | is an integer. In particular, | ||
| + | |||
| + | $$ | ||
| + | \sum _ { k= } 1 ^ \infty | ||
| − | + | \frac{c _ {k} ( n) }{n ^ {s} } | |
| + | = \ | ||
| − | + | \frac{\sigma _ {1-} s ( n) }{\zeta ( s) } | |
| + | , | ||
| + | $$ | ||
| − | where | + | where $ \zeta $ |
| + | is the Riemann [[Zeta-function|zeta-function]] and $ \sigma _ {a} $ | ||
| + | is the sum of the $ a $- | ||
| + | th powers of the divisors of $ n $. | ||
| + | Such sums are closely connected with special series for certain additive problems in number theory (cf. [[Additive number theory|Additive number theory]]); for example, the representation of a natural number as an even number of squares. S. Ramanujan [[#References|[1]]] obtained many formulas involving Ramanujan sums. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> S. Ramanujan, "On certain trigonometrical sums and their applications in the theory of numbers" ''Trans. Cambridge Philos. Soc.'' , '''22''' (1918) pp. 259–276 ((Also: Collected papers, Chelsea, reprint, 1962.))</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> G.H. Hardy, "Note on Ramanujan's trigonometrical function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077220/r07722022.png" /> and certain series of arithmetical functions" ''Proc. Cambridge Philos. Soc.'' , '''20''' (1920–1921) pp. 263–271</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> G.H. Hardy (ed.) et al. (ed.) , ''Collected papers of S. Ramanujan'' , Chelsea, reprint (1962)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> B. Volkmann, "Verallgemeinerung eines Satzes von Maxfield" ''J. Reine Angew. Math.'' , '''271''' (1974) pp. 203–213</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> E.C. Titchmarsh, "The theory of the Riemann zeta-function" , Clarendon Press (1951)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> V.I. Levin, "The life and work of the Indian mathematician Ramanujan" ''Istoriko-Mat. Issled.'' , '''13''' (1960) pp. 335–378 (In Russian)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> S. Ramanujan, "On certain trigonometrical sums and their applications in the theory of numbers" ''Trans. Cambridge Philos. Soc.'' , '''22''' (1918) pp. 259–276 ((Also: Collected papers, Chelsea, reprint, 1962.))</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> G.H. Hardy, "Note on Ramanujan's trigonometrical function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077220/r07722022.png" /> and certain series of arithmetical functions" ''Proc. Cambridge Philos. Soc.'' , '''20''' (1920–1921) pp. 263–271</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> G.H. Hardy (ed.) et al. (ed.) , ''Collected papers of S. Ramanujan'' , Chelsea, reprint (1962)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> B. Volkmann, "Verallgemeinerung eines Satzes von Maxfield" ''J. Reine Angew. Math.'' , '''271''' (1974) pp. 203–213</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> E.C. Titchmarsh, "The theory of the Riemann zeta-function" , Clarendon Press (1951)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> V.I. Levin, "The life and work of the Indian mathematician Ramanujan" ''Istoriko-Mat. Issled.'' , '''13''' (1960) pp. 335–378 (In Russian)</TD></TR></table> | ||
Revision as of 08:09, 6 June 2020
Trigonometric sums depending on two integer parameters $ k $
and $ n $:
$$ c _ {k} ( n) = \sum _ { h } \mathop{\rm exp} \left ( \frac{2 \pi n h i }{k} \right ) = \ \sum _ { h } \cos \frac{2 \pi n h }{k} , $$
when $ h $ runs over all non-negative integers less than $ k $ and relatively prime to $ k $. The basic properties of Ramanujan sums are multiplicity with respect to the index $ k $,
$$ c _ {k k ^ \prime } ( n) = c _ {k} ( n) c _ {k ^ \prime } ( n) \ \ \textrm{ if } ( k , k ^ \prime ) = 1 , $$
and also the representation in terms of the Möbius function $ \mu $:
$$ c _ {k} ( n) = \ \sum _ {d \mid ( k , n ) } \mu \left ( \frac{k}{d} \right ) d . $$
Ramanujan sums are finite if $ k $ or $ n $ is finite. In particular, $ c _ {k} ( 1) = 1 $.
Many multiplicative functions on the natural numbers (cf. Multiplicative arithmetic function) can be expanded as series of Ramanujan sums, and, conversely, the basic properties of Ramanujan sums enable one to sum series of the form
$$ \sum _ { n= } 1 ^ \infty \frac{c _ {k} ( q n ) }{n ^ {s} } f ( n) ,\ \ \sum _ { k= } 1 ^ \infty \frac{c _ {k} ( q n ) }{k ^ {s} } f ( k) , $$
where $ f $ is a multiplicative function and $ q $ is an integer. In particular,
$$ \sum _ { k= } 1 ^ \infty \frac{c _ {k} ( n) }{n ^ {s} } = \ \frac{\sigma _ {1-} s ( n) }{\zeta ( s) } , $$
where $ \zeta $ is the Riemann zeta-function and $ \sigma _ {a} $ is the sum of the $ a $- th powers of the divisors of $ n $. Such sums are closely connected with special series for certain additive problems in number theory (cf. Additive number theory); for example, the representation of a natural number as an even number of squares. S. Ramanujan [1] obtained many formulas involving Ramanujan sums.
References
| [1] | S. Ramanujan, "On certain trigonometrical sums and their applications in the theory of numbers" Trans. Cambridge Philos. Soc. , 22 (1918) pp. 259–276 ((Also: Collected papers, Chelsea, reprint, 1962.)) |
| [2] | G.H. Hardy, "Note on Ramanujan's trigonometrical function 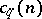 and certain series of arithmetical functions" Proc. Cambridge Philos. Soc. , 20 (1920–1921) pp. 263–271 and certain series of arithmetical functions" Proc. Cambridge Philos. Soc. , 20 (1920–1921) pp. 263–271 |
| [3] | G.H. Hardy (ed.) et al. (ed.) , Collected papers of S. Ramanujan , Chelsea, reprint (1962) |
| [4] | B. Volkmann, "Verallgemeinerung eines Satzes von Maxfield" J. Reine Angew. Math. , 271 (1974) pp. 203–213 |
| [5] | E.C. Titchmarsh, "The theory of the Riemann zeta-function" , Clarendon Press (1951) |
| [6] | V.I. Levin, "The life and work of the Indian mathematician Ramanujan" Istoriko-Mat. Issled. , 13 (1960) pp. 335–378 (In Russian) |
Ramanujan sums. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ramanujan_sums&oldid=18643