Quantum field theory, axioms for
The mathematical axiom systems for quantum field theory (QFT) grew out of Hilbert's sixth problem [a6], that of stating the problems of quantum theory in precise mathematical terms. There have been several competing mathematical systems of axioms, and below those of A.S. Wightman [a5], and of K. Osterwalder and R. Schrader [a4] are given, stated in historical order. They are centred around group symmetry, relative to unitary representations of Lie groups in Hilbert space.
Wightman axioms.
Wightman's axioms involve:
- a unitary representation $U$ of $G = \operatorname{SL} ( 2 , {\bf C} ) \rtimes {\bf R} ^ { 4 }$ as a covering of the Poincaré group of relativity, and a vacuum state vector $\psi_0$ fixed by the representation.
- Quantum fields $\varphi _ { 1 } ( f ) , \dots , \varphi _ { n } ( f )$, say, as operator-valued distributions, $f$ running over a specified space of test functions, and the operators $\varphi _ { i } ( f )$ defined on a dense and invariant domain $D$ in $\mathcal{H}$ (the Hilbert space of quantum states), and $\psi _ { 0 } \in D$.
- A transformation law which states that $U ( g ) \varphi_j ( f ) U ( g ^ { - 1 } )$ is a finite-dimensional representation $R$ of the group $G$ (cf. also Representation of a group) acting on the fields $\varphi _ { i } ( f )$, i.e., $\sum _ { i } R _ { j i } ( g ^ { - 1 } ) \varphi _ { i } ( g [ f ] )$, $g$ acting on space-time and $g [ f ] ( x ) = f ( g ^ { - 1 } x )$, $x \in \mathbf{R} ^ { 4 }$.
- The fields $\varphi_j ( f )$ are assumed to satisfy locality and one of the two canonical commutation relations of $[ A , B ] _ { \pm } = A B \pm B A$, for fermions, respectively bosons.
- Finally, it is assumed that there is scattering with asymptotic completeness, in the sense $\mathcal{H} = \mathcal{H} ^ { \text{in} } = \mathcal{H} ^ { \text{out} }$.
Osterwalder–Schrader axioms.
The Wightman axioms were the basis for many of the spectacular developments in QFT in the 1970s, see, e.g., [a1], [a2], and the Osterwalder–Schrader axioms [a3], [a4] came in response to the dictates of path-space measures. The constructive approach involved some variant of the Feynman measure. But the latter has mathematical divergences that can be resolved with an analytic continuation, so that the mathematically well-defined Wiener measure becomes instead the basis for the analysis. Two analytical continuations were suggested in this connection: in the mass-parameter, and in the time-parameter, i.e., $t \mapsto \sqrt { - 1 }t$. With the latter, the Newtonian quadratic form on space-time turns into the form of relativity, $x _ { 1 } ^ { 2 } + x _ { 2 } ^ { 2 } + x _ { 3 } ^ { 2 } - t ^ { 2 }$. One gets a stochastic process $\mathcal{X} _ { t }$ that is: symmetric, i.e., ${\cal X} _ { t } \sim {\cal X}_{ - t }$; stationary, i.e., $\mathcal{X} _ { t + s } \sim \mathcal{X} _ { s }$; and Osterwalder–Schrader positive, i.e., $\int _ { \Omega } f _ { 1 } \circ \mathcal{X} _ { t _ { 1 } } \ldots f _ { n } \circ \mathcal{X} _ { t _ { n } } d P \geq 0$, $f _ { 1 } , \ldots , f _ { n }$ test functions, $- \infty < t _ { 1 } \leq \ldots \leq t _ { n } < \infty$, and $P$ denoting a path space measure.
Specifically: If $- t / 2 < t _ { 1 } \leq \ldots \leq t _ { n } < t / 2$, then
 | (a1) |
\begin{equation*} = \operatorname { lim } _ { t \rightarrow \infty } \int \prod _ { k = 1 } ^ { n } A _ { k } ( q ( t _ { k } ) ) d \mu _ { t } ( q ( \cdot ) ). \end{equation*}
By Minlos' theorem, there is a measure $\mu$ on ${\cal D} ^ { \prime }$ such that
\begin{equation} \tag{a2} \operatorname { lim } _ { t \rightarrow \infty } \int e ^ { i q ( f ) } d \mu _ { t } ( q ) = \int e ^ { i q ( f ) } d \mu ( q ) = : S ( f ) \end{equation}
for all $f \in \mathcal{D}$. Since $\mu$ is a positive measure, one has
\begin{equation*} \sum _ { k } \sum _ { l } \overline { c } _ { k } c _ { l } S ( f _ { k } - \overline { f } _ { l } ) \geq 0 \end{equation*}
for all $c_1 , \ldots , c_n \in \mathbf{C}$, and all $f _ { 1 } , \dots , f _ { n } \in \mathcal{D}$. When combining (a1) and (a2), one can note that this limit-measure $\mu$ then accounts for the time-ordered $n$-point functions which occur on the left-hand side in (a1). This observation is further used in the analysis of the stochastic process $\mathcal{X} _ { t }$, $\mathcal{X} _ { t } ( q ) = q ( t )$. But, more importantly, it can be checked from the construction that one also has the following reflection positivity: Let $( \theta f ) ( s ) : = f ( - s )$, $f \in \mathcal{D}$, $s \in \mathbf{R}$, and set
\begin{equation*} \mathcal{D} _ { + } = \{ f \in \mathcal{D} : f \ \text { real valued, } f ( s ) = 0 \text { for } s < 0 \}. \end{equation*}
Then
\begin{equation*} \sum _ { k } \sum _ { l } \overline { c } _ { k } c_{ l} S ( \theta (\, f _ { k } ) - f _ { l } ) \geq 0 \end{equation*}
for all $c_1 , \ldots , c_n \in \mathbf{C}$ and all $f _ { 1 } , \dots , f _ { n } \in \mathcal{D} _ { + }$, which is one version of Osterwalder–Schrader positivity.
Relation to unitary representations of Lie groups.
Since the Killing form of Lie theory may serve as a finite-dimensional metric, the Osterwalder–Schrader idea [a4] turned out also to have implications for the theory of unitary representations of Lie groups. In [a3], P.E.T. Jorgensen and G. Ólafsson associate to Riemannian symmetric spaces $G / K$ of tube domain type (cf. also Symmetric space), a duality between complementary series representations of $G$ on one side, and highest-weight representations of a $c$-dual $G ^ { c }$ on the other side. The duality $G \leftrightarrow G ^ { c }$ involves analytic continuation, in a sense which generalizes $t \mapsto \sqrt { - 1 }t$, and the reflection positivity of the Osterwalder–Schrader axiom system. What results is a new Hilbert space, where the new representation of $G ^ { c }$ is "physical" in the sense that there is positive energy and causality, the latter concept being defined from certain cones in the Lie algebra of $G$.
A unitary representation $\pi$ acting on a Hilbert space $\mathcal{H} ( \pi )$ is said to be reflection symmetric if there is a unitary operator $J : \mathcal{H} ( \pi ) \rightarrow \mathcal{H} ( \pi )$ such that
- R1) $J ^ { 2 } = \operatorname{id}$;
- R2) $J \pi ( g ) = \pi ( \tau ( g ) ) J$, $g \in G$. Here, $\tau \in \operatorname { Aut } ( G )$, $\tau ^ { 2 } = \operatorname{id}$, and $H = \{ g \in G : \tau ( g ) = g \}$.
A closed convex cone $C \subset \text{q}$ is hyperbolic if $C ^ { o } \neq \emptyset$, and if $\operatorname { ad } X$ is semi-simple (cf. also Semi-simple representation) with real eigenvalues for every $X \in C ^ { o }$.
Assume the following, for $( G , \pi , \tau , J )$:
- PR1) $\pi$ is reflection symmetric with reflection $J$.
- PR2) There is an $H$-invariant hyperbolic cone $C \subset \text{q}$ such that $S ( C ) = H \operatorname { exp } C$ is a closed semi-group and $S ( C ) ^ { o } = H \operatorname { exp } C ^ { o }$ is diffeomorphic to $H \times C ^ { o }$.
- PR3) There is a subspace $0 \neq \mathcal{K} _ { 0 } \subset \mathcal{H} ( \pi )$, invariant under $S ( C )$, satisfying the positivity condition
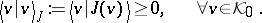 |
Assume that $( \pi , C , \mathcal{H} , J )$ satisfies PR1)–PR3). Then the following hold:
$S ( C )$ acts via $s \mapsto \widetilde{\pi} ( s )$ by contractions on $\mathcal{K}$ (the Hilbert space obtained by completion of $\mathcal{K} _ { 0 }$ in the norm from PR3)).
Let $G ^ { c }$ be the simply-connected Lie group with Lie algebra $\mathfrak { g } ^ { c }$. Then there exists a unitary representation $\tilde{\pi} ^ { c }$ of $G ^ { c }$ such that $d \tilde { \pi } ^ { c } ( X ) = d \tilde { \pi } ( X )$ for $X \in \mathfrak { h }$ and 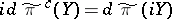 for $Y \in C$, where $\mathfrak { h } = \{ X \in \mathfrak { g } : \tau ( X ) = X \}$.
for $Y \in C$, where $\mathfrak { h } = \{ X \in \mathfrak { g } : \tau ( X ) = X \}$.
The representation $\tilde{\pi} ^ { c }$ is irreducible if and only if $\tilde{\pi}$ is irreducible.
References
| [a1] | J. Glimm, A. Jaffe, "Quantum field theory and statistical mechanics (a collection of papers)" , Birkhäuser (1985) |
| [a2] | J. Glimm, A. Jaffe, "Quantum physics" , Springer (1987) (Edition: Second) |
| [a3] | P.E.T. Jorgensen, G. Ólafsson, "Unitary representations of Lie groups with reflection symmetry" J. Funct. Anal. , 158 (1998) pp. 26–88 |
| [a4] | K. Osterwalder, R. Schrader, "Axioms for Euclidean Green's functions" Comm. Math. Phys. , 31/42 (1973/75) pp. 83–112;281–305 |
| [a5] | R.F. Streater, A.S. Wightman, "PCT, spin and statistics, and all that" , Benjamin (1964) |
| [a6] | A.S. Wightman, "Hilbert's sixth problem: Mathematical treatment of the axioms of physics" F.E. Browder (ed.) , Mathematical Developments Arising from Hilbert's Problems , Proc. Symp. Pure Math. , 28:1 , Amer. Math. Soc. (1976) pp. 241–268 |
Quantum field theory, axioms for. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quantum_field_theory,_axioms_for&oldid=55338